可适应稀疏度变化的非均匀范数约束水声信道估计算法
2014-03-01伍飞云周跃海童峰方世良
伍飞云,周跃海,童峰,方世良
(1.厦门大学 海洋与地球学院,福建 厦门361005;2.东南大学 信息科学与工程学院,江苏 南京210018)
0 引言
由于具有典型的时间-频率双重选择性扩展,水声信道的高效、准确估计极具挑战性[1-4],而其冲激响应中往往仅有少数几个大值系数,其余大部分则为0 或接近0 的小值系数,结合稀疏特性改善信道估计性能具有重要的理论意义和实用价值,已引起广泛关注[5-7]。
其中,匹配追踪(MP)算法[8]将残留信号用于最大化混合矩阵列向量的相关运算,对稀疏信道抽头进行逐个估计,但该算法无法保证理论最优解,且由于过完备字典中原子数目太大,而每次匹配选取最佳原子的个数只有一个,使得选取过程中匹配选取的次数过多,MP 算法的计算复杂度高;同时,经典MP 算法需已知稀疏信道的大值抽头数,因此不能有效地应用到实际场合。
文献[9 -10]将稀疏水声信道多径径数、时延及幅度组成多径参数模型,并引入进化优化算法对非线性多径参数模型进行全局寻优,但由于多径参数模型的解空间将随着径数的增多而急剧增大,该方法在信道多径径数较多时性能明显下降。
Zeng 等[11]采用时延-多普勒扩展模型分别结合MP、投影梯度方法改善了对块速时变稀疏信道的估计性能,但由于需在时延-多普勒二维参数空间寻优,当信道多径时延扩展大或多普勒扩展大时运算复杂度将急剧增高。如在某些典型水声信道中该方法将要求信道参数长度增至1 000 维[12]。
[13 -19]先后将范数约束(l1范数或l0范数)引入到最小均方(LMS)代价函数中,从而以较低的运算复杂度开销加快算法对稀疏系统中非零系数的收敛,特别是适合于具有较长多径时延扩展的水声信道。然而,当水声信道中由于工作位置、深度及水文条件等变化造成多径稀疏度发生变化时,由于l1范数和l0范数约束项本身并无针对稀疏度的调整因子,该类算法的性能将受到较大影响;同时,l1范数和l0范数算法约束项对大值抽头的检测实际上仍依赖于某种硬门限,这也造成了这类算法对微弱多径的检测能力不高。
针对这一问题,Wu 等[20]将似p 范数[6]引入LMS 代价函数,导出p 值可变的似p 范数约束LMS算法,通过p 值的调整改善了对不同稀疏程度的适应性能,但由于似p 范数迭代需要进行复杂的小数指数运算,在实际应用中算法的实现受一定限制。
Wu 等[21]引入非均匀范数约束并推导出由一系列l0或l1范数元素组成的非均匀范数约束LMS(NNCLMS)系数迭代公式,通过权向量中大小不同的幅值产生不同l0、l1组合形式的非均匀范数进行不同稀疏程度下的约束调整,从而避免使用硬阈值造成的对微弱多径的检测性能下降,并可提供对稀疏度变化信道的适应能力;同时,该算法在降低运算复杂度的同时,提高了收敛速度、降低了稳态失调误差。但文献[21]中未给出该算法的收敛性证明。本文分析了NNCLMS 算法的收敛性能,并利用该算法提供的稀疏度适应性进行稀疏度变化水声信道估计,不同接收深度水声信道的仿真和海试实验验证了该算法可提高水声信道估计中对稀疏度变化的容忍性。
1 NNCLMS 算法
1.1 算法描述
定义非均匀范数[21]为
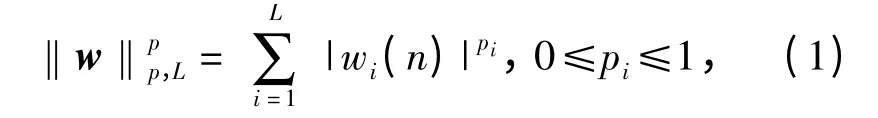
式中:w(n)表示n 时刻待优化的滤波器抽头系数,即w(n)中每L 个元素采用不同的p 值并求和组成非均匀范数,L 表示滤波器长度。定义代价函数为

则根据梯度优化,信道估计器的权系数迭代公式为
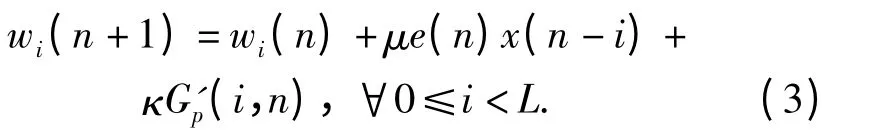
(2)式和(3)式中:κ =μγ >0 是步长参数和平衡因子相乘得到的参数;e(n)为期望信号d(n)与滤波器输出信号xT(n)w(n)之差,表示为e(n)=d(n)-xT(n)w(n);G'p(i,n)为约束项的梯度,
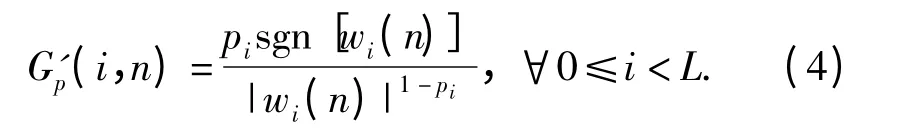
采用权系数向量的期望E[|wi(n)|]作为“大”“小”值wi(n)的区分界限,则可借助非均匀范数中的pi参数进行估计偏差和稀疏约束作用的折中优化,对“小”值wi(n),权系数迭代中范数约束产生一个零吸引作用加快收敛;而对“大”值wi(n),范数约束引入的零吸引作用趋于消失以减小估计偏差。即:
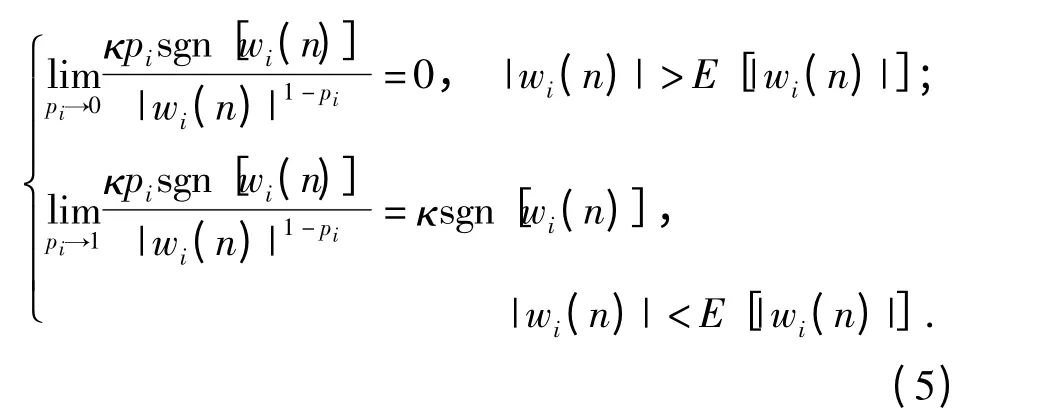
由此分析,最终得到滤波器向量更新公式为
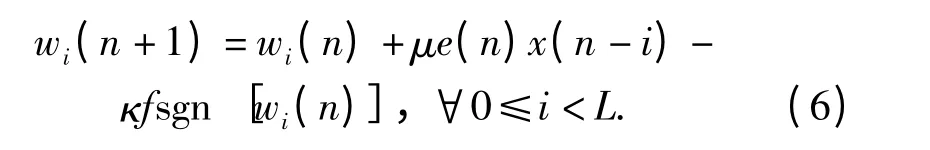
(6)式中,f 定义为
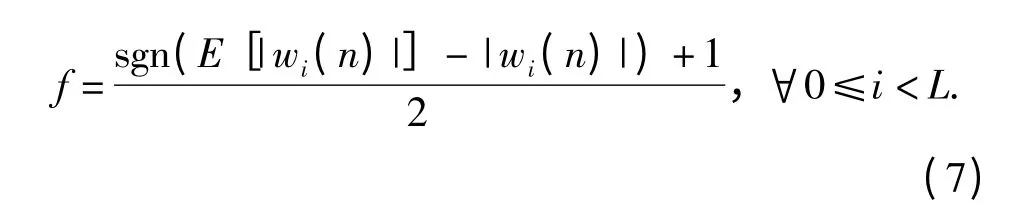
同时,在(7)式基础上可对非均匀范数约束项进行复加权以进一步减少估计偏差,因此,NNCLMS算法权系数更新表达式为
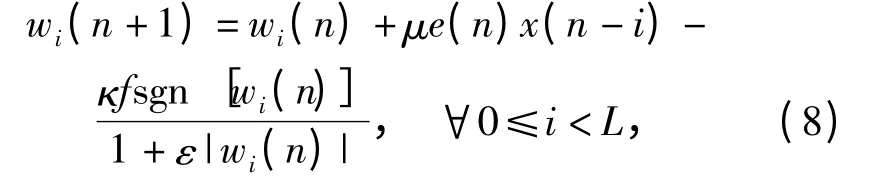
式中:ε >0 是一个控制复加权强度的常数。
NNCLMS 算法中参数κ、ε 对算法性能有一定影响:参数κ 反映了零吸引的力度[13-17],参数κ 越大,引起的稳态失调也越大,当然其收敛速度也越快。因此参数κ 的选择需要在收敛速度和收敛质量之间权衡;复加权系数ε 表明复加权的力度以减少估计算法的有偏程度,同时,复加权系数ε 越大,零吸引力则越弱。因此复加权系数ε 需要在减弱有偏程度和零吸引力之间权衡。
本文算法与标准LMS 算法及l0-LMS[16]、l1-LMS[19]这两种经典范数约束LMS 算法的计算复杂度比较如表1所示,由此可见,与经典l0-LMS、l1-LMS 算法相比,本文算法仅带来少量的计算量增加。
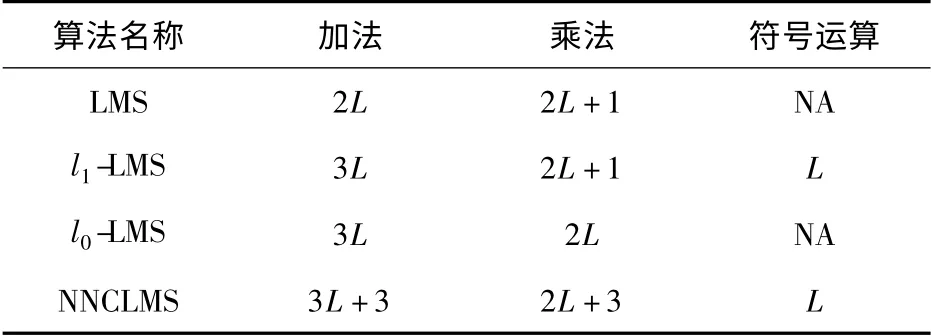
表1 各算法每次迭代的计算量Tab.1 The amounts of calculation of different algorithms in each iteration
1.2 算法收敛性分析
本文对NNCLMS 算法进行收敛性分析。定义抽头误差向量为
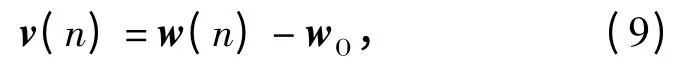
式中:wO是经典LMS 算法的最优抽头值。(9)式左右两边同时减去wO,结合(8)式,可得
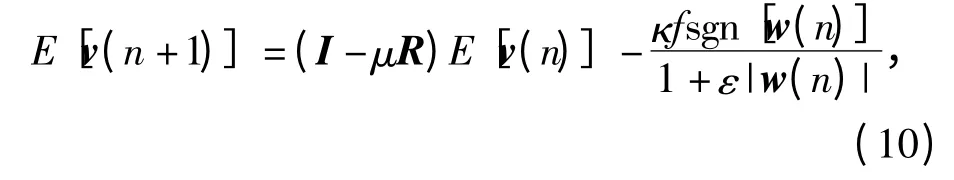
式中:R = x(n)x(n)T,I 是单位矩阵;而向量是介于和之间的一个常数项。因此,如果算法的步长值μ 满足条件:

式中:λmax是矩阵(I-μR)的最大特征值,则E[v(n)]收敛。
由此证明了NNCLMS 算法的收敛性。本文将引入该算法以适应对不同接收深度导致的水声信道稀疏度变化。
2 仿真实验
本文设计数值仿真实验通过不同深度导致的水声信道不同稀疏度分析NNCLMS 算法性能并与LMS、l0-LMS、l1-LMS 等传统算法进行对比。实验采用稀疏比(SR)量化评估仿真水声信道的稀疏度,SR定义为非零抽头的个数除以全部抽头的个数得到的比值。
仿真实验采用BELLHOP 射线模型产生仿真水声信道[22],设置为:均匀声速,距离为1 000 m,水深200 m,发射深度100 m,接收深度分别为100 m、60 m,20 m.声线最大数目设置为800 条,发射声源角度设置为-60° ~60°. 每条声线最小搜索角为0.15°.仿真中设定每隔5 000 个码元改变接收机深度从而产生3 个对应不同接收深度的水声信道。实验中发射随机码元,码元波特率8 k.
图1给出了20 m、60 m、100 m 3 个不同深度下收发本征声线。由图1可以看出,随着深度变化,水声信道径数不断增加造成稀疏度变化。仿真水声信道阶数为250,则其稀疏程度变化可通过SR 值的变化来体现:在1、5 001、10 001 点的位置对应的SR值为2/250、3/250、5/250. 该3 个阶段对应的仿真水声信道响应如图2所示。为了便于性能比较,实验中,各算法的估计器长度设置为250. 调整各算法的参数使得各算法最小均方差(MSE)最优,对应的各参数见表2所示。
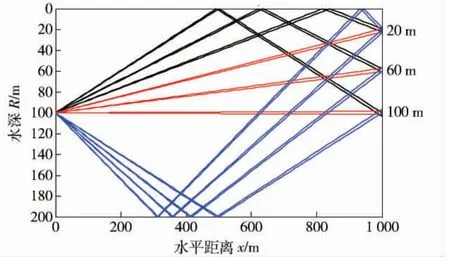
图1 BELLHOP 模型中3 个不同接收深度对应的声线Fig.1 BELLHOP-model-based multipaths at 3 receiving depths
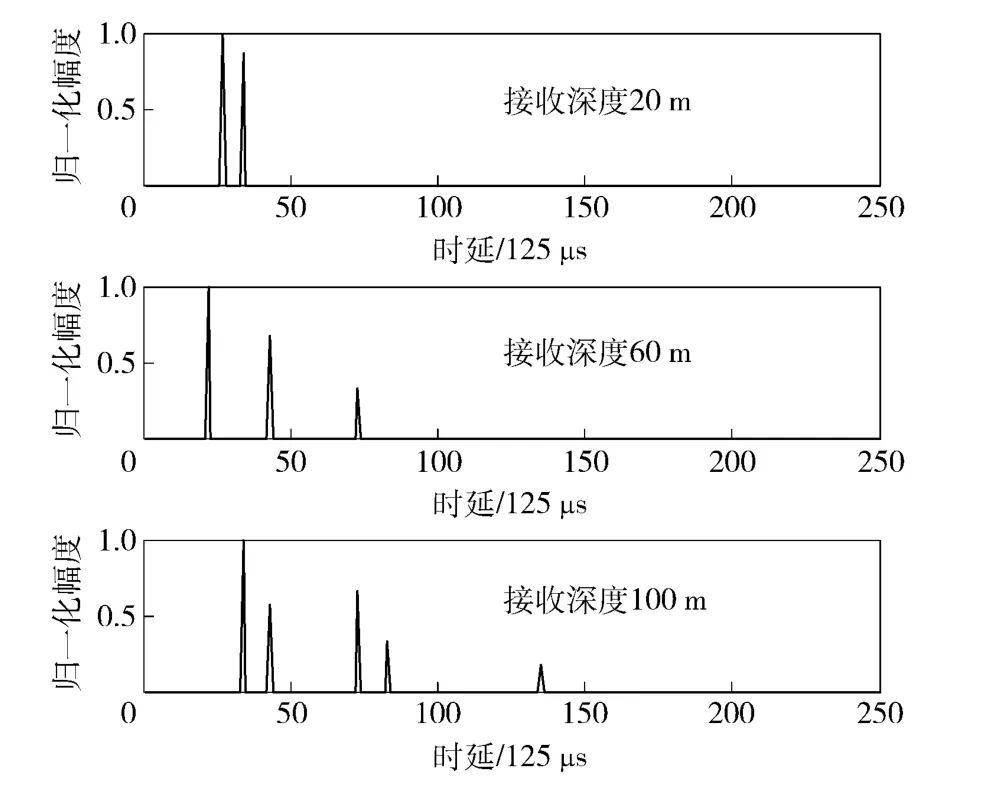
图2 BELLHOP 模型中3 个不同接收深度对应的信道响应Fig.2 BELLHOP model-based multipath time delay channels at 3 receiving depths
表2 仿真实验各算法参数Tab.2 Parameters of different algorithms in simulation
仿真结果如图3所示,仿真中因信道稀疏度设置分别在点1、5 001、10 001 点处,该信道的变化引起算法MSE 在对应点的突变,随后各自5 000 点长度的迭代中各算法收敛精度各有差异,从图3可以看出,施加稀疏约束后的LMS 各类改进版本都比经典LMS 算法表现更好,尤其是NNCLMS 比l0-LMS、l1-LMS 性能更加优越。其中,可见固定范数约束类算法(l0-LMS、l1-LMS)在SR 增加时,该类算法通过稀疏约束项获取的性能改善减小;而范数约束项包含调节机制的NNCLMS 算法由于可通过对范数约束的调节来适应信道的不同稀疏程度,表明本算法对不同的稀疏性具有更好的适应性。
同时,对水声信道的时变特性,信道估计算法的收敛速度体现了对时变信道的跟踪性能,图3体现出本文算法收敛性优于l1-LMS 和LMS 算法,与l0-LMS 收敛速度类似,而本文算法MSE 性能表现最优。
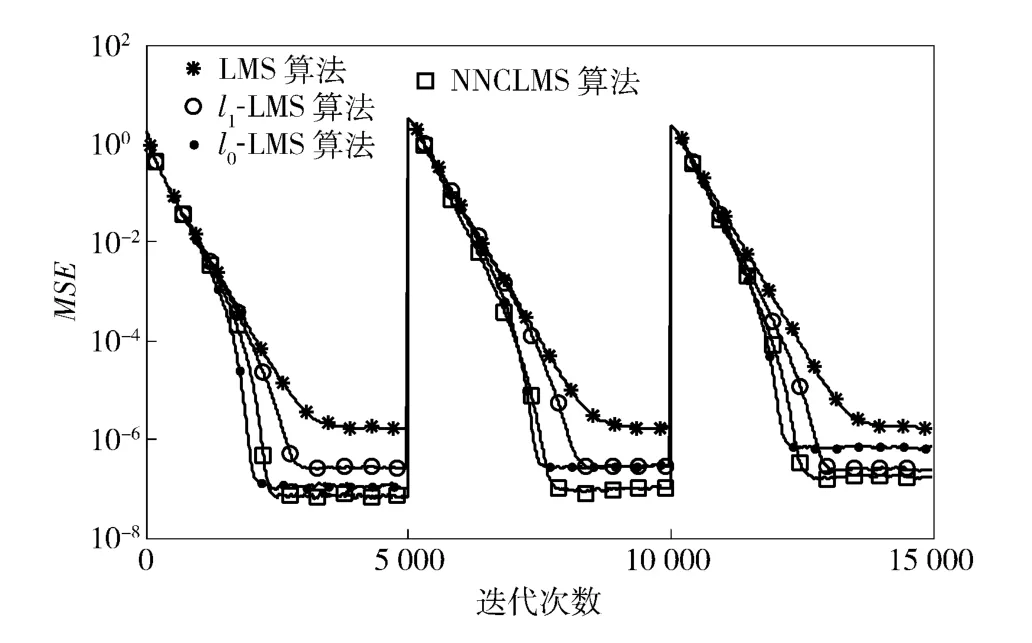
图3 不同SR 下不同算法的MSE 曲线Fig.3 MSE curves with the different SRs
3 海试实验
本文算法的海试实验采用正交相移键控(QPSK)调制信号,信号载波频率为16 kHz,采样率为96 kbit/s,数据率6.4 kbit/s,发射随机序列。实验海域为厦门五缘湾,平均水深8 m,发射机和接收机之间的距离为2 km;发射换能器深度7 m,接收换能器初始深度4 m,在实验过程中接收换能器进行了深度调整,造成信道多径稀疏度发生变化。
由于信道估计的目的是通过估计获取信道响应以构造信道均衡器改善通信性能,信道估计的准确度将决定均衡器的性能以及通信质量。因此,本文海试实验中各类算法所获得的信道响应将通过线性最小均方误差(LMMSE)均衡器来实现码元恢复,并采用误比特率(BER)作为指标进行信道估计算法性能评估。LMMSE 均衡的输入输出关系可以写成[11]:
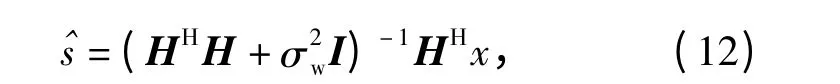
式中:I 表示单位矩阵;H 为算法估计获取的水声信道冲激响应;σw表示噪声能量的参数。由于LMMSE均衡器是基于信道估计结果获得,以输出信噪比和误码率从通信角度可评估信道估计方法性能。
实验中LMMSE 均衡器长度为100,与信道估计器阶数相同,采用1/2 分数间隔结构。由于实验水声信道表现出时变特性,每50 个符号保存一次信道估计结果用于更新LMMSE 均衡器以适应信道时变;同时,考虑到在每次信道估计更新后的50 个符号内进行的是固定系数LMMSE 均衡,无法补偿此时间范围内信道时变造成的残余多径,为此在LMMSE 均衡器后级联一个阶数为6、遗忘因子0.995 的1/2 分数间隔结构RLS 均衡器用来对这部分信道时变进行辅助补偿,抑制残余多径。此RLS均衡器在独立工作时无法达到均衡效果。
为方便进行性能对比,在LMMSE 均衡实验中各信道估计算法根据将均衡器稳定收敛后输出信噪比调至大致相同进行设置,具体参数见表3所示。MP 算法[8]设定的多径径数为5.
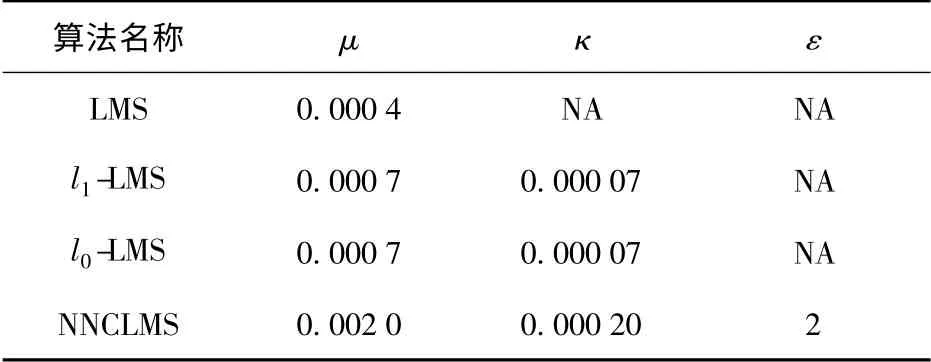
表3 LMMSE 均衡实验各算法参数Tab.3 Parameters of LMMSE equalizers of different algorithms
图4(a)~图4(e)分别给出了LMS、NNCLMS、l1-LMS、l0-LMS,以及MP 算法[8]的信道估计结果,图4(f)给出了以QPSK 随机发射序列作为参考信号进行窗长为1 s、滑动步长0.25 s 的滑动窗匹配滤波获取的时变信道响应结果。从图4(f)中可以看出,在数据开始约0.7 s 处,由于换能器深度调整的原因呈现较明显的多径稀疏分布变化,在图4(f)信道响应的时延扩展约3 ms 处从两个较明显多径变化为一个较强多径,同时在12 ms 的时延扩展范围内存在4 条较弱多径。
从图4可以看出:LMS 算法估计结果较好地体现了信道的结构、径数变化,但收敛较慢,且输出明显的估计噪声;相对LMS 算法,采用稀疏约束的l0-LMS,l1-LMS、NNCLMS 以及MP 算法对信道响应非零抽头处的噪声成分具有明显的抑制作用,其中l0-LMS、l1-LMS 显示出对强多径的检测性能,但对弱多径估计效果较差;MP 算法估计结果分布在信道实际多径及其邻近位置,且弱多径未被充分检测;NNCLMS 算法则体现了较快的收敛速度,对估计噪声的抑制,以及在检测强多径的同时对弱多径的检测性能。
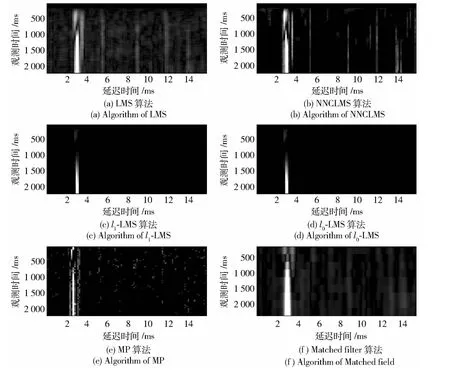
图4 各算法水声信道估计结果图Fig.4 The estimated results of underwater acoustic channels
实验中为了反映信道稀疏度变化条件下LMMSE 均衡的性能,每隔200 个符号测量一次输出信噪比以评估均衡效果。图5给出了海试实验LMMSE 均衡器输出信噪比SNR 曲线,从图5可看出:信道多径结构变化前:使用各估计算法获取的信道响应构造LMMSE 均衡器时,LMS 算法对应的LMMSE 均衡器输出信噪比提升速度较慢,采用稀疏约束的l0-LMS、l1-LMS、NNCLMS 以及MP 算法则对应较快的收敛速度,其中NNCLMS 略好于另外3 种算法,与仿真部分结论基本一致,MP 算法因为未检测出微弱多径且引入一定噪声,收敛后输出信噪比仍较低。

图5 海试实验中基于信道估计的LMMSE 均衡器输出信噪比性能Fig.5 The output SNRs of channel estimation-based LMMSE equalizer
图6给出了海试实验中对应图5的各算法误码率(BER)评价性能对比情况,可以看出:信道多径结构变化前,使用各估计算法获取的信道响应构造LMMSE 均衡器时,LMS 算法对应的LMMSE 均衡器对应的BER 较大,采用稀疏约束的l0-LMS、l1-LMS、NNCLMS 以及MP 算法则能较快降低BER,其中NNCLMS 的BER 略低于另外3 种算法,该结果与数值仿真以及图5的结论基本一致。

图6 海试实验中基于信道估计的LMMSE 均衡器的误比特率性能Fig.6 The output BERs of channel estimation-based LMMSE equalizer
在信道由于接收换能器深度变化导致稀疏度变化期间:LMS 算法由于对信道强、弱多径不加分辨进行迭代,其对应LMMSE 均衡器性能受多径稀疏分布变化的影响较小,但非零抽头处大量估计噪声造成其输出信噪比及误比特率均出现整体偏差;由于未能检测出较弱多径,在多径结构变化期间l0-LMS、l1-LMS 算法对应均衡性能呈现明显的恶化;而本文NNCLMS 算法由于可根据权值大小改变非均匀范数中l0、l1元素的分布从而改善对稀疏度变化的适应性,并能较好地检测出信道中的弱多径分量,在所有比较算法中本文算法构造LMMSE 均衡器的输出信噪比和误比特率性能均受多径稀疏度变化影响最小,体现了对多径稀疏度变化较好的适应能力。
4 结论
为了提高稀疏度变化条件下水声信道的估计性能,本文引入NNCLMS 算法并对其进行收敛性分析,该算法通过在LMS 代价函数中引入一系列l0或l1范数元素组成的非均匀范数约束项,并根据抽头系数的大小而给予不同的约束,从而以较小的运算开销改善对不同稀疏度的适应性。在信道稀疏度变化条件下的仿真和海试实验验证了本文算法在水声信道估计中应用的优越性。
参考文献(References)
[1] Li W,Preisig J C. Estimation of rapidly time-varying sparse channels[J]. IEEE Journal of Oceanic Engineering,2007,32(4):927 -939.
[2] Stojanovic M. Retrofocusing techniques for high rate acoustic communications[J]. Journal of the Acoustical Society of America,2005,117(3):1173 -1185.
[3] Stojanovic M. Efficient processing of acoustic signals for high-rate information transmission over sparse underwater channels[J].Physical Communication,2008,1(2):146 -161.
[4] Kalouptsidis N,Mileounis G,Babadi B,et al. Adaptive algorithms for sparse system identification[J]. Signal Processing,2011,91(8):1910 -1919.
[5] Angelosante D,Bazerque J A,Giannakis G B. Online adaptive estimation of sparse signals:where RLS meets the l1-norm[J].IEEE Transactions on Signal Processing,2010,58(7):3436 -3447.
[6] Rao B D,Delgado K K. An affine scaling methodology for best basis selection[J]. IEEE Transactions on Signal Processing,1999,47(1):187 -200.
[7] Naylor P A,Cui J,Brookes M. Adaptive algorithms for sparse echo cancellation[J]. Signal Processing,2006,86(6):1182 -1192.
[8] Cotter S F,Rao B D. Sparse channel estimation via matching pursuit with application to equalization[J]. IEEE Transactions on Communications,2002,50(3):374 -377.
[9] 童峰,许肖梅,方世良. 一种单频水声信号多径时延估计算法[J]. 声学学报,2008,33(1):62 -68.TONG Feng,XU Xiao-mei,FANG Shi-liang. Multipath time-delay estimation of underwater acoustic sinusoidal signals[J]. Acta Acustica,2008,33(1):62 -68. (in Chinese)
[10] 陈东升,李霞,方世良,等. 基于参数模型和混合优化的时变水声信道跟踪[J]. 东南大学学报:自然科学版,2010,40(3):459 -463.CHEN Dong-sheng,LI Xia,FANG Shi-liang,et al. Tracking of time-varying underwater acoustic channels based on multipath parameter model and hybrid optimization[J]. Journal of Southeast University:Natural Science Edition,2010,40(3):459 -463.(in Chinese)
[11] Zeng W J,Xu W. Fast estimation of sparse doubly spread acoustic channels[J]. Journal of the Acoustical Society of America,2012,131(1):303 -317.
[12] Konstantinos P,Mandar C. New sparse adaptive algorithms based on the natural gradient and the l0-norm[J]. IEEE Journal of Oceanic Engineering,2013,38(2):323 -332.
[13] Gu Y,Jin Y,Mei S. l0norm constraint LMS algorithm for sparse system identification[J]. IEEE Signal Processing Letters,2009,16(9):774 -777.
[14] Jin J,Gu Y,Mei S. A stochastic gradient approach on compressive sensing signal reconstruction based on adaptive filtering framework[J]. IEEE Journal of Selected Topics in Signal Processing,2010,4(2):409 -420.
[15] 曲庆,金坚,谷源涛. 用于稀疏系统辨识的改进l0-LMS 算法[J]. 电子与信息学报,2011,33(3):604 -609.QU Qing,JIN Jian,GU Yuan-tao. An improved l0-LMS algorithm for sparse system identification[J]. Jounal of Electronics&Information Technology,2011,33(3):604 - 609. (in Chinese)
[16] Su G,Jin J,Gu Y,et al. Performance analysis of l0norm constraint least mean square algorithm[J]. IEEE Transactions on Signal Processing,2012,60(5):2223 -2235.
[17] Chen Y,Gu Y,Hero A O. Sparse LMS for system identification[C]∥IEEE International Conference on Acoustics,Speech and Signal Processing. Taibei,Taiwan:IEEE,2009:3125 -3128.
[18] Shi K,Shi P. Adaptive sparse Volterra system identification with l0-norm penalty[J]. Signal Processing,2011,91(10):2432 -2436.
[19] Shi K,Shi P. Convergence analysis of sparse LMS algorithms with l1-norm penalty based on white input signal[J]. Signal Processing,2010,90(12):3289 -3293.
[20] Wu F Y,Tong F. Gradient optimization p-norm-like constraint LMS algorithm for sparse system estimation[J]. Signal Processing,2013,93(4):967 -971.
[21] Wu F Y,Tong F. Non-uniform norm constraint LMS algorithm for sparse system identification[J]. IEEE Communications Letters,2013,17(2):385 -388.
[22] Kostas S,Paolo C,Michele Z. The throughput of underwater networks:analysis and validation using a ray tracing simulator[J].IEEE Transactions on Wireless Communications,2013,12(3):1108 -1117.
