水下航行器壳体结构多目标优化设计研究

董华超，宋保维，王鹏

(西北工业大学 航海学院，陕西 西安710072)

0 引言

传统的水下航行器(AUV)壳体设计往往利用经验公式［1］，估算出壳板，肋骨等多处的应力，得到壳体最大强度和稳定性，过程繁复、精度不高。随着未来AUV 工作环境向大深度的发展，设计要求变得愈加复杂，仅凭经验估算，已不能满足设计者的要求。随着有限元分析软件(ANSYS)的日趋成熟，有限元仿真技术在AUV 壳体设计中得到了发展［2］，通过该技术能准确求得壳体中最大处应力，壳体失稳临界压力等重要参数，对于大深度AUV 壳体设计具有重要意义。但是有限元仿真使得计算精度提高的同时也相应降低了计算效率。随着设计变量以及设计目标的增多，利用有限元分析解决AUV 壳体多目标优化问题计算量十分庞大。结合有限元分析寻求一种合适的近似策略，在提高计算精度的同时计算效率令人满意成为了当务之急。李亦文等提出利用有限元分析采样，最小二乘法构造响应面来解决车辆低速碰撞吸能结构的优化设计［3］;甘文彪等提出利用计算流体力学(CFD)技术获得实验点，构造自适应响应面［4］对高超声速飞行器尾喷管进行优化设计。他们结合了高精度有限元计算以及代理模型的构造，但是在自适应过程中针对多目标优化问题并没有进行深入研究。

本文针对以上情况提出一种基于自适应响应面法的大深度AUV 壳体结构多目标优化方法，利用实验设计(DOE)得到初始采样点，有限元分析计算响应值，构建代理模型，通过提出的一种空间采样方法，在Pareto 解中重获采样点补充响应面，使其全局近似精度满足设计要求，并利用灰色关联处理Pareto 解，得到各目标值得“好坏程度”，模拟实际专家对各目标赋权，得到满意设计。给出一套完整的AUV 壳体结构多目标自动优化设计流程，并与传统经验公式得到结果进行对比，具有实际工程意义。

1 多目标自适应响应面法

本文介绍的多目标自适应响应面法，是针对传统的自适应响应面法解决多目标问题时提出的，该方法在每次迭代得到的Pareto 解中利用一种空间采点方法均匀取样，能在使结果满足精度的同时减少仿真次数。

1.1 自适应响应面法

自适应响应面法［5-6］的基本思想是先通过较少的样本点构造近似精度不高的一阶响应面，确定寻优方向后，在最优值附近区域内重新取样，并将新的样本点引入设计空间，这样便可以逐步构造更高阶次的样本点，在后续的迭代中优化高精度响应面重新获得新的设计点，循环往复直到满足精度要求后停止。

传统的单目标自适应响应面优化［7］往往是在每一次迭代得到的最优解附近重新采点。而多目标优化结果往往不能得到单一的最优解，而是一个Pareto 解集。因此本文考虑在Pareto 解集中合理均匀取点，来完善响应面。

考虑响应面的回归系数表达式为

式中:φ=［1，x1， xN，x21，x1x2， x1xN， x2N］.

现依据DOE 得到S 个初始设计点构造得到二阶模型回归系数为as，已知矩阵为φs，新增一Pareto解XPareto向量，其响应值为yPareto，矩阵变为

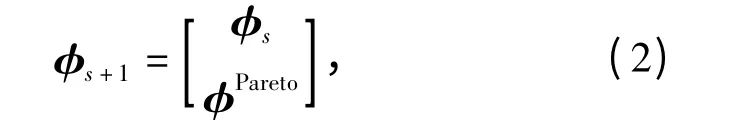
式中:φPareto=［φ1(XPareto)，φ2(XPareto)， φNB(XPareto)］，且NB 为基项φi(XPareto)的个数，这里等于1.

新的回归系数向量as+1的递推公式为

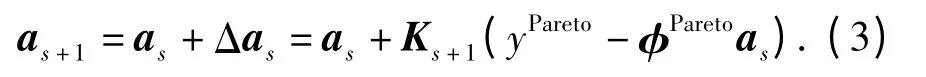
记Cs=(φTsφs)-1，(3)式中Ks+1和Cs+1可由以下递推公式计算:

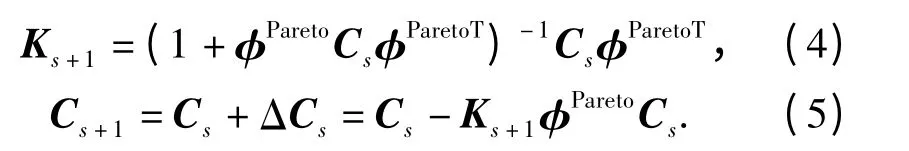
通过每次从响应面优化得到的Pareto 解中均匀取点后，按上式求得新的回归系数。

对每次得到的响应面进行误差分析判断全局近似精度，定义如下:

经过反复迭代后直到局部精度满足(7)式停止。

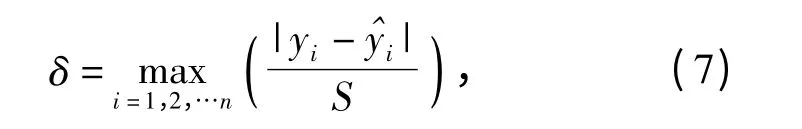
(6)式、(7)式中:yi为实测值;为响应面估计值;y为实测值的平均值;S 为测试样本集的标准差。

1.2 空间采点法

自适应循环迭代过程每一步都会产生大量的Pareto 解，对整个Pareto 解集进行高精度有限元仿真，需要消耗大量时间，难以实现。文中基于分层采样法的思想［8］提出一种空间采点法可以尽可能均匀地在Pareto 解集中采点，在满足近似精度的同时，减少仿真次数。

假设有两个目标，优化得到的Pareto 最优前沿近似分布在一条曲线上。算法步骤如下:

1)首先利用(8)式寻找原点到最优前沿上最近的一点。

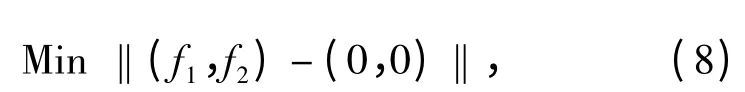
根据(8)式得到(fcenter1，fcenter2)作为中心点。以该点为圆心，R 为半径作圆。

2)计算Pareto 解集中与该圆轮廓线距离小于Δd 的点集。

式中:D=‖(f1，f2)-(fcenter1，fcenter2)‖表示点到圆心的距离。

3)通过第二步求得n 个满足条件的点。

F={(f(1)1，f(1)2)，(f(2)1，f(2)2)…(f(n)1，f(n)2)}.

计算每个点到剩下n-1 个点的距离:

式中:d(i)(j)表示第i 个点到第j 个点的距离。通过d矩阵可以判断出圆周上各点在周向的疏密关系。统计每个点的n -1 个相对距离中小于Δd 的个数作为Nd.

4)如果某点处的Nd大于0，说明有Nd+1 个点聚集在一起，取其中任意一个作为代表点，其他舍去;如果Nd等于0 直接选取。

5)半径增加R，重复1 ～4 步的操作，直到Pareto前沿范围内的点全部包含进圆内为止。

6)下一次迭代采点，适当改变R 的大小重复1 ～5 步的操作。

随着目标的增多，相应增加(8)式～(10)式的维数即可。

2 基于多标度赋权求偏好解

对Pareto 解进行加权求和时，不同目标量纲不同，数量级也不一样。往往希望先得到每个目标Pareto 解的“好坏”程度。因此本文在赋权之前对每个目标的Pareto 解进行灰色关联分析，具体计算过程参见文献［9］。

传统AUV 壳体结构设计中，对于多个目标“孰优孰劣”问题，往往需要请教在这个领域有丰富工程经验的专家。而专家在给出偏好信息时，通常只能采用例如“目标A 比目标B 重要”等这样的语言形式来表达目标之间的相对重要性。因此本文结合AUV 壳体结构设计时实际专家赋权情况，采用一种多级标度赋值法把目标间的相对偏好量化为各目标的重要性因子［10］。如表1所示。

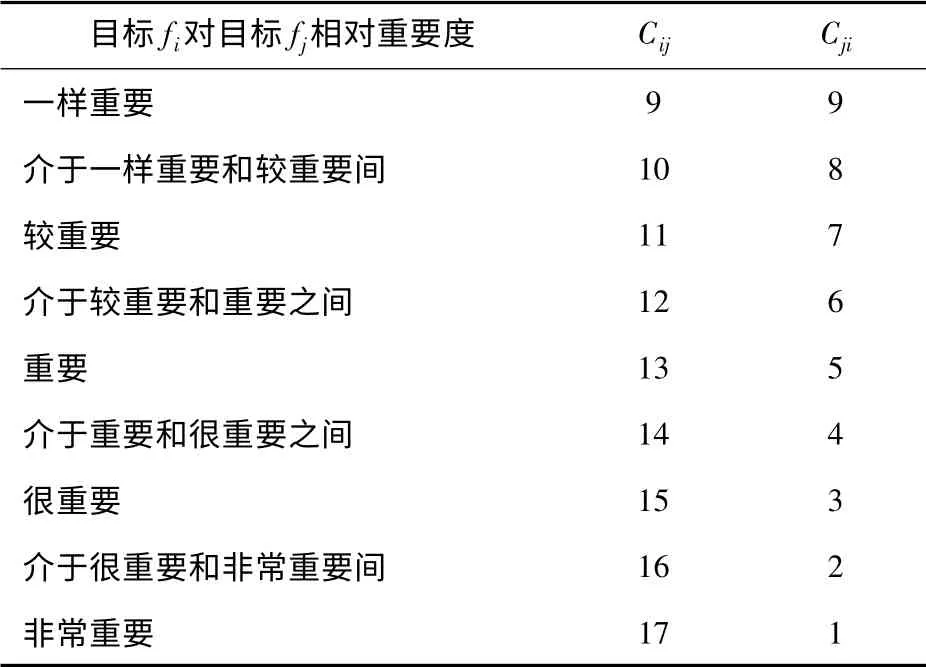
表1 多级标度赋值表Tab.1 Multilevel-scale evaluation

通过赋值矩阵C 计算目标fi的重要性因子wi.

式中:SLi=为目标fi对其余所有目标的标度优序数。

3 多目标优化流程

基于本文提出的自适应响应面方法AUV 壳体结构多目标优化流程如图1所示。

图1中，DOE 采用正交实验设计，响应面从一阶开始逐渐提高精度。全局精度通过(6)式判断，局部精度通过(7)式判断。

4 AUV 壳体结构优化模型

4.1 壳体结构自动化参数建模

图2所示为AUV 一小段壳体的纵向剖切简图。以壳体厚度t，肋骨间距l，肋骨宽度t2，肋骨长度l2作为设计变量，半径R =0.324 m，长L =1.5 m.在UG 中进行几何自动化参数建模，产生x_t 文件。通过ANSYS 的命令流录制文件，自动分析计算。

屈服极限σs=343 MPa，弹性模量E =71 GPa，泊松比μ =0.33，密度ρ =2 700 kg/m3.载荷条件为:

1)外压:本文所设计的耐压壳体工作在500 m水深，壳体外压载荷pj=5.5 MPa;

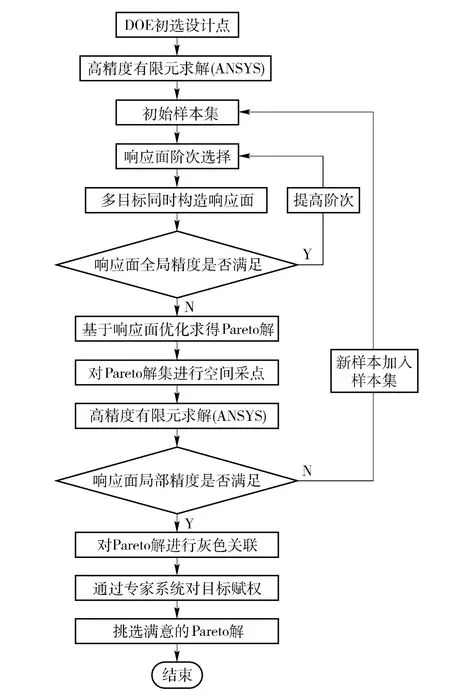
图1 优化流程示意图Fig.1 Flow chart of multi-objective optimization

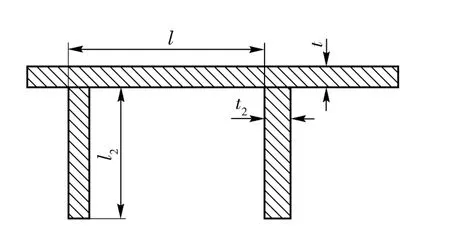
图2 AUV 矩形壳体肋骨结构简图Fig.2 AUV shell structure with rectangular ribs

2)约束:一端全固定约束，另一端只允许轴向移动;

3)轴向载荷:只允许轴向移动端加轴向载荷，其值由最大横截面积和壳体端面面积的比乘以外压载荷得到。

4.2 壳体结构优化模型建立

以t、l、t2、l2为设计变量;壳体最大应力σmax最小，壳体失稳临界压力pc最大，壳体质量m 最小为优化目标;壳体最大应力小于0.85 倍的屈服极限，且壳体失稳临界压力大于1.2 倍外载荷为约束［1］。给出优化模型为

式中:n(l)为肋骨根数。

5 优化求解

用经验公式优化得到最优解作为初始点，并在该点附近进行正交DOE，根据第3 节的多目标优化流程，自动计算。计算前先对3 个目标Pareto 解进行统一无量纲处理(其中σmax先求倒数，使得3 个目标统一最小最好)，Δd 设置为0.01。且采点半径R分别选取0.04，0.06，0.08，0.1.随迭代，从0.04 到0.1 循环采集，这样保证尽可能均匀地采集到Pareto解，以半径为0.1 时的空间采点示意图如图3所示。根据精度要求设置R2小于0.999，δ 小于0.01.采用经典多目标优化算法NSGA2，种群大小设置50，种群代数设置100.经过8 次迭代，107 次仿真计算得到3 个目标的响应面如下:

求出m、σmax关于Pareto 解中最小值的灰色关联度，pc关于Pareto 解中最大值的灰色关联度，如图4所示。

AUV 壳体设计专家给出目标间的相对重要程度为:m 比σmax重要的多;m 比pc重要;pc比σmax稍微重要一点。根据表1得到赋权矩阵为

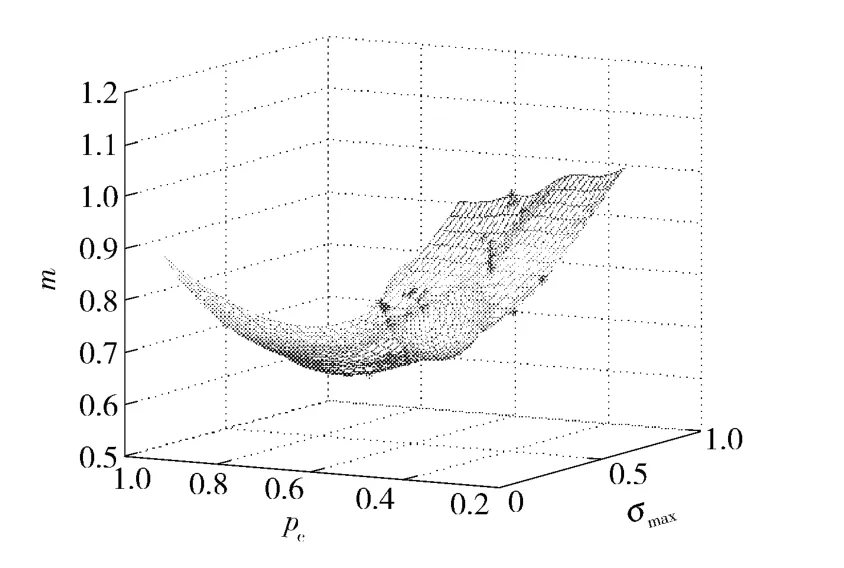
图3 空间采点示意图Fig.3 Schematic diagram of spatial sampling points

图4 Pareto 解经灰色关联后示意图Fig.4 Prareto results after grey relational analysis

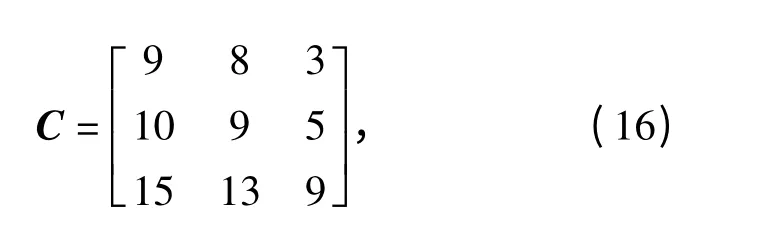
得到w1为11/54，w2为15/54，w3为28/54.定义总体性能指标F 如下:

式中:G(·)表示灰色关联度。最终根据总体性能指标找到满意解。仿真结果如图5所示。

壳体质量m 的减小势必导致壳体处最大应力σmax变大和壳体失稳临界压力pc减小。根据表2数据可知本文设计得到的优化结果:壳体最大应力σmax在满足约束的情况下增加41.58%，壳体失稳临界压力pc在满足约束的情况下减小25%，壳体质量m 减小20.5%，总体性能提高14.67%.综上可知，该方法在满足近似精度的同时，结果可行有效，具有实际的工程意义。

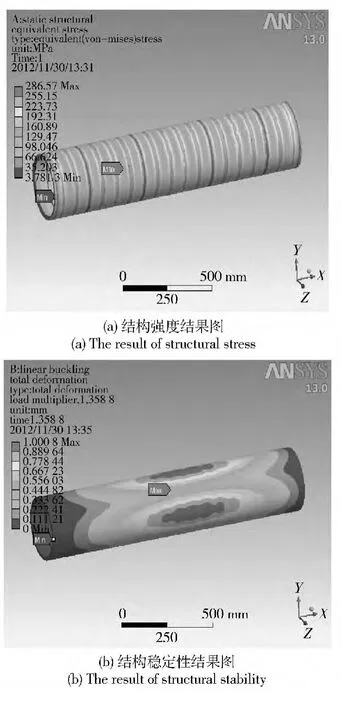
图5 优化仿真结果图Fig.5 Diagram of simulation of optimal solution

表2 经验公式结果与优化后设计结果对比Tab.2 Comparison of original and optimized resualts

6 结论

针对大深度AUV 壳体结构多目标优化问题，以有限元仿真技术为基础，利用多项式近似方法构造代理模型，通过提出的空间采点法实现响应面的更新。本文与传统利用经验公式计算壳体结构的设计方法进行了对比，优化使得最终壳体结构多目标问题的总体性能提高了14.67%.本文对壳体结构有限元仿真自动优化技术提出了一个完整设计框架，为水下航行器壳体结构设计领域提出一种新的设计思路，具有工程参考意义。

对于未来计算新型的复杂壳体结构，本文还需要从优化算法，近似方法两方面改进，来满足模型高度非线性的特点。

References)

［1］ 宋保维，李楠.iSIGHT 在多目标优化问题中的研究［J］.火力与指挥控制，2008，33(6):133 -136.SONG Bao-wei，LI Nan.Application research of iSIGHT in solving multi-objective design optimization problems［J］.Fire Control and Command Control，2008，33(6):133 -136.(in Chinese)

［2］ 何惠江，李楠.基于APDL 的鱼雷壳体结构参数化建模［J］.鱼雷技术，2010，18(4):246 -248.HE Hui-jiang，LI Nan.Parametric modeling of torpedo shell structure based on APDL［J］.Torpedo Technology，2010，18(4):246 -248.(in Chinese)

［3］ 李亦文，徐涛，徐天爽，等.车身低速碰撞吸能结构的优化设计［J］.北京理工大学学报，2010，30(10):1175 -1179.LI Yi-wen，XU Tao，XU Tian-shuang，et al.Optimal design of energy-absorbing structure of autobody under low-speed crash［J］.Transactions of Beijing Institute of Technology，2010，30(10):1175 -1179.(in Chinese)

［4］ 甘文彪，阎超.高超声速飞行器后体/尾喷管优化设计［J］.北京航空航天大学学报，2011，37(11):1440 -1445.GAN Wen-biao，YAN Chao.Afterbody/nozzle optimal design of hypersonic vehicle［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(11):1440 -1445.(in Chinese)

［5］ Shan S，Wang G G.Survey of modeling and optimization strategies for high-dimensional design problems［C］∥12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference.British Columbia:AIAA，2008:5842.

［6］ Wang D，Naterer G F，Wang G.Adaptive response surface method for thermal optimization:application to aircraft engine cooling system［C］∥8th AIAA/ASME Joint Thermophysics and Heat Transfer Conference.St Louis:AIAA，2002:1 -10.

［7］ 兰凤崇，钟阳，庄良飘，等.基于自适应响应面法的车身前部吸能部件优化［J］.汽车工程，2010，32(5):404 -408.LAN Feng-chong，ZHONG Yang，ZHUANG Liang-piao，et al.Optimization of energy-absorbing members in front-end of car body based on adaptive response surface method［J］.Automative Engineering，2010，32(5):404 -408.(in Chinese)

［8］ Saltelli A，Ratto M.Global sensitivity analysis:the primer［M］.England:John Wiley ＆ Sons Ltd，2008:53 -99.

［9］ 胡成亮，刘全坤，王强，等.基于灰色关联和模糊逻辑的齿轮锻模多目标优化设计［J］.中国机械工程，2007，18(14):1739 -1742.HU Cheng-liang，LIU Quan-kun，WANG Qiang，et al.Multi-objective optimal design of the gear forging die based on grey relational andfuzzy logic［J］.China Mechanical Engineering，2007，18(14):1739 -1742.(in Chinese)

［10］ Cvetkovic D，Parmee I C.Preferences and their application in evolutionary multiobjective optimization［J］.IEEE Transactions on Evolutionary Computation，2002，6(1):42 -45.