基于扰动观测器的导引头隔离度抑制方法研究
2014-03-01徐娇王江宋韬胡宽容
徐娇,王江,宋韬,胡宽容
(1. 北京理工大学 宇航学院,北京100081;2. 西北工业集团有限公司,陕西 西安710043)
0 引言
导引头的主要功能是跟踪目标并测量目标运动信息,提供给弹上控制系统使其按照预定的制导律控制导弹飞向目标[1]。在导弹飞行过程中,弹体姿态扰动会部分耦合到导引头中,从而使输出的目标视线角速度存在误差[2]。导引头隔离度表征了导引头对弹体扰动的去耦能力,隔离度Rdr定义如下:

国内外关于导引头隔离度的研究一般仅关注其对导引头输出精度的影响[3-8],但隔离度的主要问题在于其不仅恶化了导引头输出,还会严重降低导弹的制导精度[9]。因此,如何对隔离度进行有效抑制是目前迫切需要解决的问题。工程上常采用柔化导线、降低动静摩擦等工艺方法减小干扰力矩以降低隔离度。Masten[10]指出构建带宽较宽的稳定回路可以降低干扰力矩的影响,然而导引头稳定回路带宽与平台导引头电机、角速率传感器等硬件密切相关,不能无限制的增加。隔离度在线抑制是指在导弹飞行过程中,利用弹载传感器信息对隔离度进行实时辨识和补偿,达到提高导引头弹目视线角速度输出精度,改善导弹制导性能的目的。该技术代表了隔离度抑制技术的发展方向。国内外对隔离度在线抑制技术的研究还基本处于空白状态,仅Lin等[11]设计了神经网络算法对隔离度模型进行辨识,并利用前馈算法进行补偿,由于算法较为复杂,且导弹飞行时间较短,难以实现实时在线抑制。
扰动观测器(DOB)常用于估计控制系统的干扰信号,并利用估计结果对控制系统进行补偿[12-14]。利用DOB 对真实的弹目视线角度进行估计,并将估计值作为导引头输出引入到制导系统中,从而降低隔离度对导弹制导系统的影响,实现对隔离度的抑制。
本文建立了平台导引头隔离度模型,研究了闪烁噪声和接收机热噪声输入下隔离度对制导精度的影响,设计了基于DOB 的隔离度在线抑制算法,分析了DOB 建模误差、导引头探测器输出频率以及测量误差对隔离度抑制效果的影响。
1 平台导引头隔离度模型
平台导引头结构框图如图1所示。
图1中,ua为电机输入电压,Ea为反电动势,TM为电机输出转矩,TD为干扰力矩引起的负载转矩,为导引头光轴转动角速度,为弹体摆动角速度,为导引头框架角速度,为导引头输出。其他符号定义及典型参数取值如表1所示。
可以看出,由于反电动势和干扰力矩的存在,弹体摆动角速度被引入到导引头回路中。因此,引起导引头隔离度的因素为反电动势和干扰力矩。
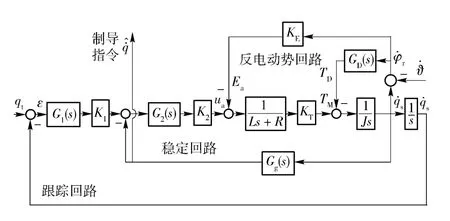
图1 平台导引头结构框图Fig.1 Block diagram of gimbaled seeker
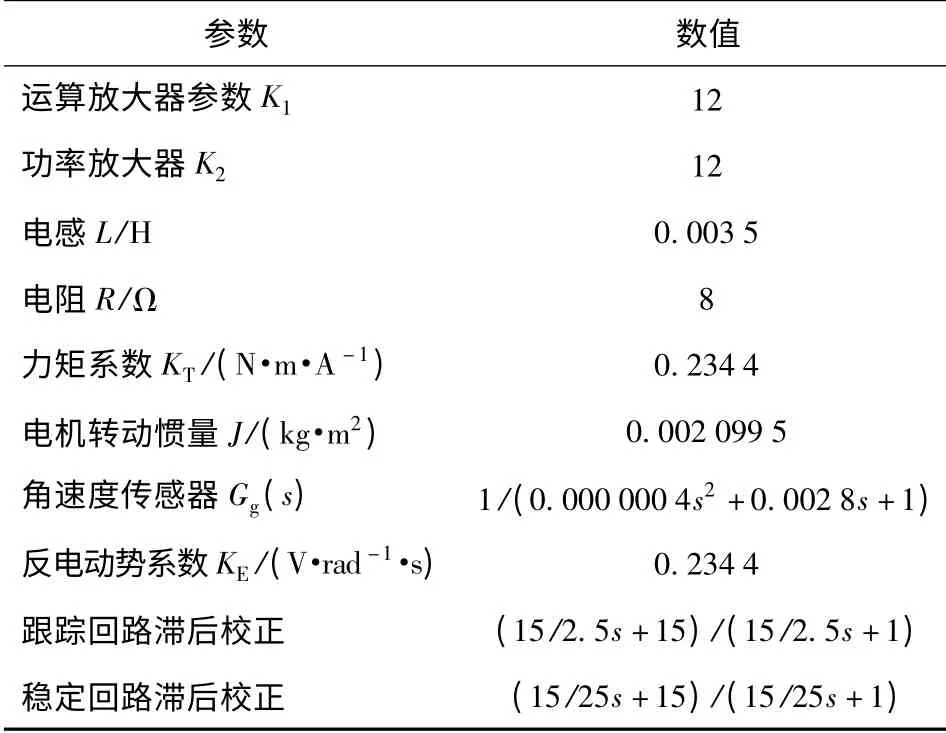
表1 典型平台导引头参数Tab.1 Parameters of typical gimbaled seeker
首先忽略干扰力矩,分析反电动势系数对隔离度的影响。取表1所示的典型参数。可以得到不同频率处反电动势引起的隔离度幅值,如表2所示。

表2 反电动势作用下不同频率处隔离度幅值Tab.2 Amplitude of DRR with back electromotive force at different frequencies
由表2可知,由反电动势引起的隔离度很小(不大于1.0%),反电动势不是造成隔离度的主要因素,因此引起隔离度问题的主要因素为弹簧力矩和阻尼力矩。
平台导引头干扰力矩主要由弹簧力矩TN和阻尼力矩Tω组成。弹簧力矩是由平台与基座之间的导线拉扯引起的,与导引头框架角相关;阻尼力矩是由转动连接处的动静摩擦引起的,与导引头框架角速度相关。真实的弹簧力矩和阻尼力矩为非线性,图2为典型导引头的非线性弹簧力矩和摩擦力矩模型[11]。
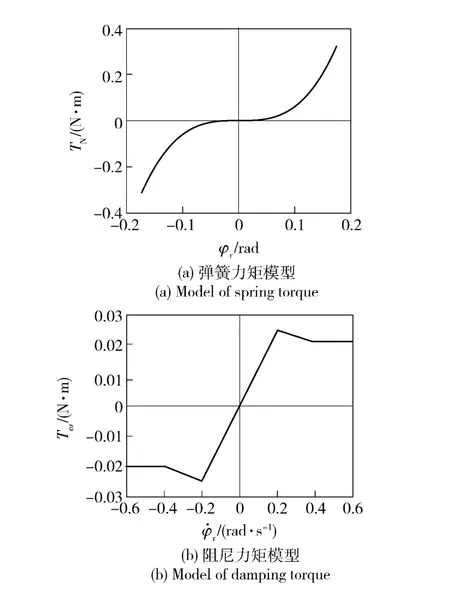
图2 平台导引头干扰力矩非线性模型Fig.2 Nonlinear modesl of disturbance torque
在导弹飞行中,导引头框架角和框架角速度一般处于较小的范围内,在此范围内,弹簧力矩和阻尼力矩的非线性特性不明显。利用线性化的干扰力矩模型研究隔离度问题能够简化分析,且结果可以为工程实践提供一定的理论指导[7]。线性化后的干扰力矩模型如图3所示。
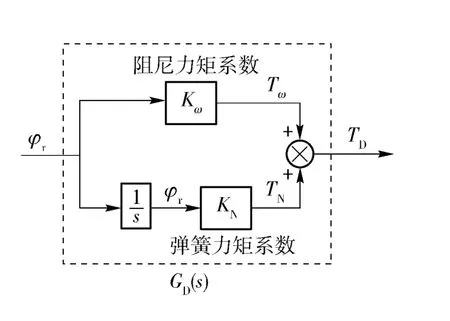
图3 线性化的干扰力矩模型Fig.3 Linearized disturbance torque
单独由弹簧力矩引起的隔离度传递函数为

单独由阻尼力矩引起的隔离度传递函数为

图4和图5分别给出了不同的KN和Kω对隔离度频域特性的影响。从中可以看出,随着KN和Kω的增加,相位基本不变,幅值增加。

图4 弹簧力矩系数对隔离度频域特性的影响Fig.4 Effect of spring torque coefficient on DRR

图5 阻尼力矩系数对隔离度频域特性的影响Fig.5 Effect of damping torque coefficient on DRR
在一定输入频率下,隔离度幅值与干扰力矩系数近似呈线性关系。在工程应用中,KN和Kω无法直接获得,目前隔离度指标约束和测试中关注弹体频率处的隔离度幅值。设典型的弹体自振频率为2 Hz,在后续分析中,可以用2 Hz 处的隔离度幅值Rdr(简称隔离度幅值)表征KN和Kω.
2 导引头隔离度对制导精度的影响
导弹在飞行过程中受到各种干扰因素的影响,包括闪烁噪声、接收机内部热噪声等[15]。在不考虑导引头隔离度问题时,很多学者研究了这些干扰对脱靶量的影响[15-16],但在干扰输入下导引头隔离度与制导系统脱靶量的关系方面的研究非常少。在闪烁噪声和接收机内部热噪声输入下,平台导引头隔离度作用时的比例导引制导系统框图如图6所示。
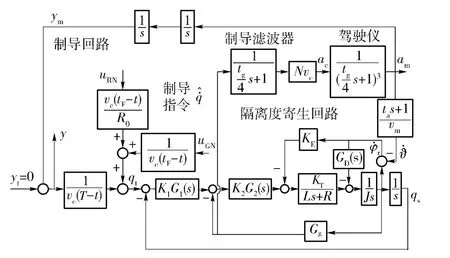
图6 干扰输入下隔离度作用时的制导系统框图Fig.6 Block diagram of guidance system under the action of DRR with disturbance input
图6中:yt为目标横向位移,此时不考虑目标机动的影响,设为0;ym为导弹横向位移;y 为横向脱靶量;vc为导弹和目标相对运动速度;vm为导弹飞行速度;tF为制导时间;T 为导弹飞行所需时间;t 为导弹实际飞行时间,定义剩余制导时间tgo=tF-t;制导系统用4 次1 阶环节表示,其中制导滤波器1 次,自动驾驶仪3 次;tg为制导系统时间常数;N 为比例导引系数;ta为导弹攻角时间常数;ac为导弹过载指令;am为导弹过载输出;uGN为标准差σGN的闪烁白噪声输入;uRN为标准差σRN的接收机白噪声输入;R0为参考距离。利用伴随法[17]分析隔离度对制导精度的影响,定义yGN为目标闪烁输入引起的脱靶量;yRN为接收机噪声输入引起的脱靶量。取典型空空导弹参数:vc/vm=2,N =4. 当tF/tg=10 时,图7给出了目标闪烁噪声输入下yGNΦ-1/2GN曲线。图8给出了接收机热噪声输入下yRNR0Φ-1/2RN曲线。

图7 目标闪烁噪声输入下yGNΦ-1/2GN 变化曲线Fig.7 Curves of yGNΦ-1/2GN due to glint noise input

图8 接收机热噪声输入下yRNR0Φ-1/2RN 变化曲线Fig.8 Curves of yRNR0Φ-1/2RN due to receiver noise input
在目标闪烁噪声输入下,制导系统脱靶量yGN与噪声功率谱密度ΦGN的平方根呈正比;在接收机热噪声输入下,制导系统脱靶量yRN与噪声功率谱密度ΦRN的平方根呈正比,与参考距离R0呈反比。
在弹簧力矩引起的隔离度作用下,随着隔离度幅值Rdr的提高,制导系统脱靶量增加。在阻尼力矩引起的隔离度作用下,在Rdr较小时,脱靶量基本不变;随着Rdr的增加,脱靶量迅速增加。与弹簧力矩引起的隔离度相比,阻尼力矩引起的隔离度对制导系统制导精度的影响较小。
3 基于DOB 的隔离度抑制算法设计
在隔离度作用下,平台导引头输出中包含两部分分量:一为真实的弹目视线角速度;二为隔离度问题引起的弹体扰动分量。将存在弹体扰动分量的导引头输出引入到制导系统中,降低了制导精度。通过设计DOB 估计模型,对真实的弹目视线角度进行估计,并将估计值作为导引头输出引入到制导系统中,可以降低隔离度对导弹制导系统的影响,实现对隔离度的抑制。
3.1 DOB 模型建立
DOB 常用于估计控制系统的扰动信号,并利用附加的前馈或反馈通路对扰动进行补偿,常用的DOB 结构如图8所示。
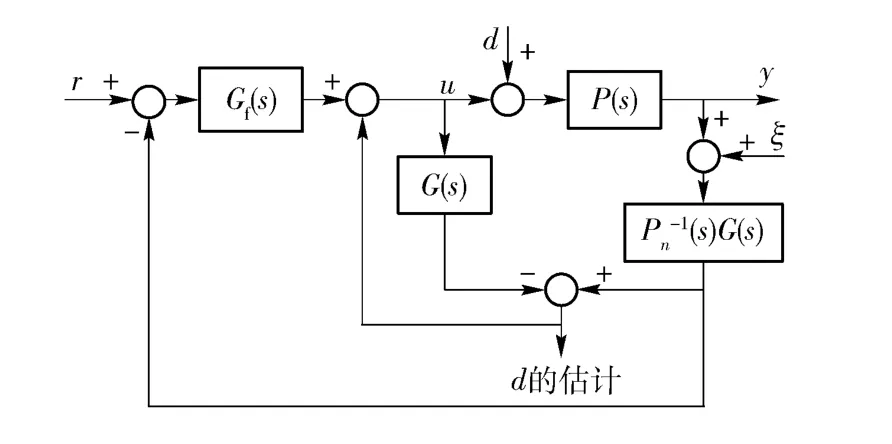
图8 常用的DOB 结构图Fig.8 Block diagram of DOB
图8中,r 为DOB 输入,Gf(s)反馈补偿器,G(s)为低通滤波器,d 为干扰输入,P(s)为实际被观测系统,Pn(s)为被观测系统的数学模型,ξ 为模型与实际系统的偏差,y 为扰动DOB 输出。
在图8所示的DOB 结构中,取消反馈控制回路,将真实的弹目视线角速度作为DOB 的干扰输入,实现对的实时估计,并将估计结果作为导引头输出传递给导弹制导控制系统,从而达到了抑制隔离度的目的。DOB 估计模型如图9所示。
对图1所示的平台导引头模型进行简化。由于反电动势系数KE很小,对导引头输出和隔离度影响可以忽略,设角速率陀螺Gg(s)≈1,令Gω1(s)=K1G1(s),Gω2(s)=KTK2G2(s)/(JLs2+JRs). 简化后的导引头模型如图10所示。

图9 弹目视线角速度DOB 估计模型Fig.9 DOB model for estimating LOS angular rate
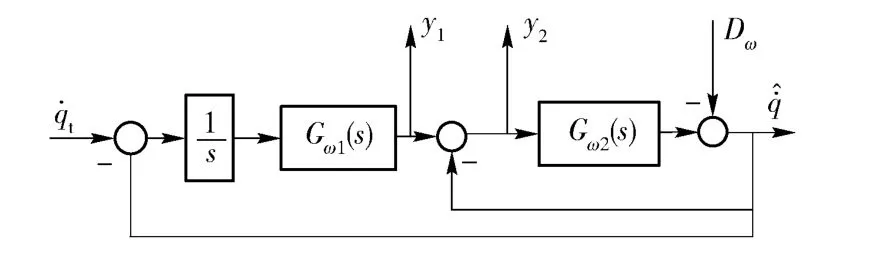
图10 平台导引头简化模型Fig.10 Simplified model of gimbaled seeker
图10中:y1为稳定回路指令信号;y2为稳定回路误差信号,由稳定回路指令与导引头角速率陀螺负反馈信号叠加后得到;Dω为干扰力矩TD引起的附加的光轴旋转角速度,Dω=TD/Js.
由图10可知,导引头稳定回路闭环传递函数为

跟踪回路传递函数为

由干扰量Dω输入到导引头输出信号的传递函数为

进一步推导可得
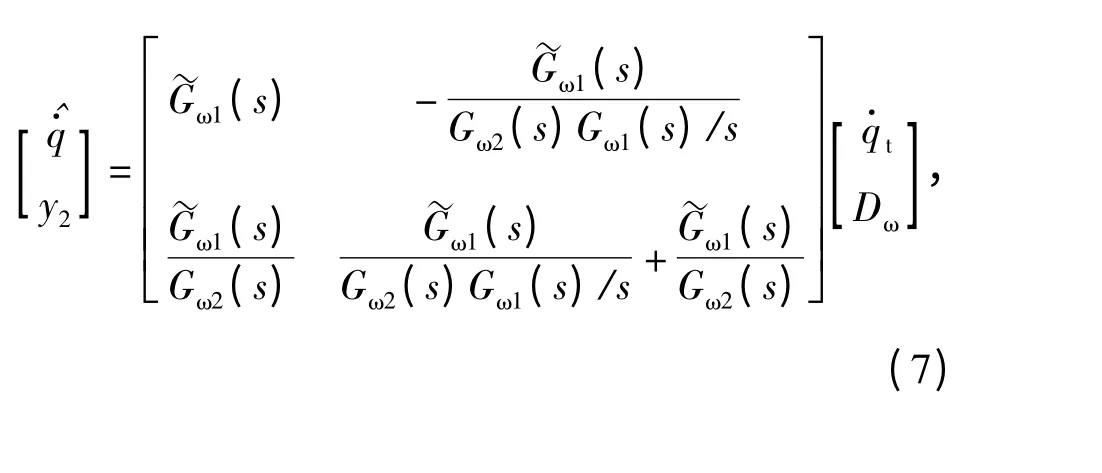
容易推导出
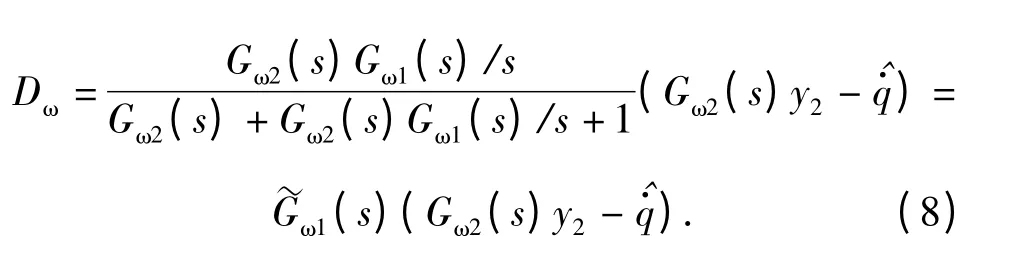
图9中的中间信号a 可以表示为
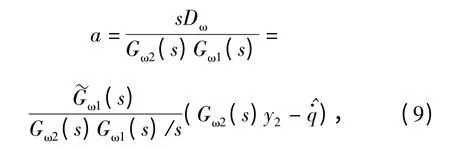
将中间信号a 作为DOB 估计模型输入u. (9)式表明,DOB 输入u 可以通过采集导引头输出信号以及稳定回路误差信号y2进行综合后得到。
假设导引头模型与真实系统相同,可以得到

由于Pn-1(s)分子的阶数大于等于分母的阶数,难以保证物理可实现性,因此,引入低通滤波器G(s)使DOB 可实现。取G(s)为
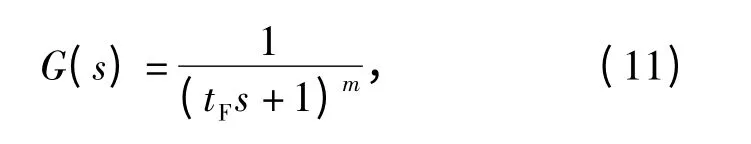

从干扰量Dω到估计值的传递函数为
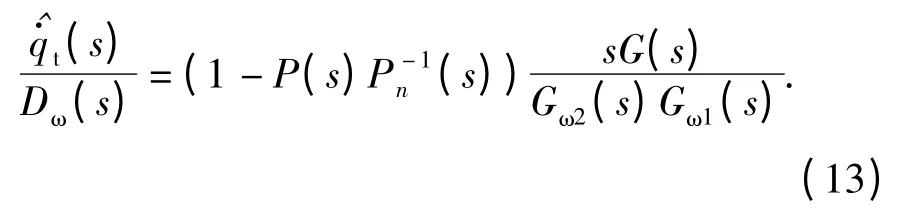
不考虑导引头建模误差时,P(s)=Pn(s),得到即估计值等于输入经过一个滞后环节;(s)/Dω(s)=0,即估计值中完全消除了隔离度的干扰。
3.2 DOB 估计精度和隔离度抑制效果分析
由(5)式得到平台导引头闭环传递函数为

(14)式中分母和分子阶数相差3 阶,则低通滤波器传递函数选为
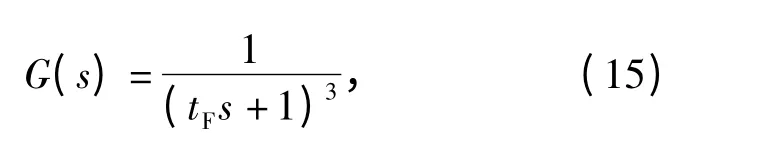
进一步可以得到

采用DOB 方法在线抑制隔离度时,弹上计算机实时采集导引头输出信号以及稳定回路误差信号y2,生成中间信号a,表达式如下:


图11 DOB 对的估计结果Fig.11 DOB estimated results for
在真实使用环境中,由于存在导引头建模不确定性、探测器输出频率及导引头传感器测量噪声等因素,会对弹目视线角速度的估计精度产生影响。下面将利用数学仿真进行分析。
由于导引头建模存在一定的不确定性,当稳定回路与跟踪回路开环增益发生波动时,DOB 估计效果如图12所示。图12表明,稳定回路和跟踪回路开环增益的变化会降低DOB 估计精度,DOB 估计值中难以完全消除隔离度的影响。

图12 开环增益波动对DOB 估计效果的影响Fig.12 Effect of open-loop gain on estimated results
探测器输出频率一般有20 Hz、50 Hz、100 Hz 3 种[18],等效为跟踪回路上分别引入50 ms、20 ms以及10 ms 延时环节,图13给出了引入延时后DOB对弹目视线角速度的估计效果。图13表明,探测器输出频率越低,DOB 估计精度越差。目前常用的探测器输出频率一般在50 Hz 以上,此时探测器延时对DOB 估计效果影响较小。

图13 探测器输出频率对DOB 估计效果的影响Fig.13 Effect of detector output frequency on estimated results
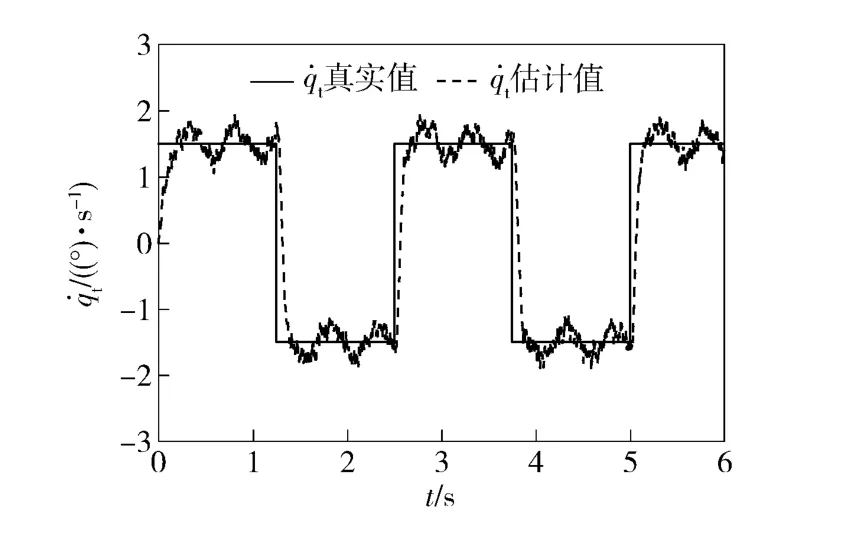
图14 测量噪声对DOB 估计效果的影响Fig.14 Effect of measurement noise on estimated results
将DOB 估计结果引入到制导系统中,研究初始速度方向误差输入下DOB 对隔离度的抑制效果,图15给出了引入DOB 后的的制导系统框图。
制导系统仿真参数如表3所示。

图15 引入DOB 的制导系统框图Fig.15 Block diagram of guidance system with DOB method

表3 采用DOB 的制导系统仿真参数Tab.3 Simulation parameters of guidance system using DOB method

图16 tF =5 s 时DOB 对弹目视线角速度估计结果Fig.20 DOB estimated results for LOS angular rate for tF =5 s
由图16可以看出,DOB 可以有效估计真实的弹目视线角速度,但估计结果受干扰因素的影响较大。
不同制导时间tF下制导系统的脱靶量曲线如图17所示。

图17 不同tF下DOB 对脱靶量的影响Fig.17 Effect of DOB on miss distance at different tF
图17结果表明,将DOB 估计的弹目视线角速度作为平台导引头的输出,可以有效地抑制非线性干扰力矩引起的隔离度对制导系统的影响。
4 结论
本文建立平台导引头隔离度模型,分析了其对导弹制导系统脱靶量的影响,并设计了基于DOB 的隔离度抑制算法,得到以下结论:
1)导引头平台与弹体之间的弹簧力矩和阻尼力矩是引起平台导引头隔离度的主要因素。
2)隔离度不仅仅会增加导弹制导系统脱靶量,与阻尼力矩引起的隔离度相比,弹簧力矩对制导精度的影响更为严重。
3)基于DOB 的隔离度抑制算法能够较为准确地对弹目视线角速度进行估计,将估计结果代入到制导系统中,能够实现隔离度的有效抑制;导引头建模不准确、探测器输出频率降低以及测量噪声的增加会降低DOB 的估计精度,减弱隔离度的抑制效果;干扰力矩非线性对DOB 估计和隔离度抑制效果基本没有影响。
References)
[1] Zipfel P H . Modeling and simulation of aerospace vehicle dynamics[M]. Florida:American Institute of Aeronautics and Astronautics,2000.
[2] Taylor J H,Price C F. Direct statistical analysis of missile guidance system via CADET[R]. Massachusetts:Analytic Sciences Corporation,1976.
[3] Kwon Y S,Hwang H Y,Choi Y S. Stabilization loop design on direct drive gimbaled platform with low stiffness and heavy inertia[C]∥International Conference on Control,Automation and Systems 2007. Seoul,Korea:IEEE,2007:320 -325.
[4] 穆虹. 防空导弹雷达导引头设计[M]. 北京:宇航出版社,1996.MU Hong. Design of air defense missile seeker[M]. Beijing:China Astronautic Publishing House,1996.(in Chinese)
[5] Bhattacharya R N,Tao T V,Sadhu S. Control structures and properties of missile seekers[J]. Journal of the Institution of Engineers:Electrical Engineering Division,2002,82(3):253-261.
[6] 朱华征,范大鹏,马东玺,等. 导引头伺服系统隔离度与测试[J].光学精密工程,2009,17(8):1993 -1998.ZHU Hua-zheng,FAN Da-peng,MA Dong-xi,et al. Disturbance isolation index of seeker servo system and its test[J]. Optics and Precision Engineering,2009,17(8):1993 -1998.(in Chinese)
[7] 李富贵,夏群利,崔晓曦,等. 导引头隔离度寄生回路对视线角速度提取的影响[J]. 宇航学报,2013,34(8):1072 -1077.LI Fu-gui,XIA Qun-li,CUI Xiao-xi,et al. Effect of seeker disturbance rejection rate parasitic loop on line of sight rate extraction[J]. Journal of Astronautics,2013,34(8):1072 - 1077. (in Chinese)
[8] Kwon Y S,Hwang H Y,Choi Y S. Stabilization loop design on direct drive gim-baled platform with low stiffness and heavy inertia[C]∥International Conference on Control,Automation and Systems.Seoul Korea:IEEE,2007.
[9] 杜运理,夏群利,祁载康. 导引头隔离度相位滞后对寄生回路稳定性影响研究[J]. 兵工学报,2011,32(1):28 -32.DU Yun-li,XIA Qun-li,QI Zai-kang. Research on effect of seeker disturbance rejection rate with phase lag on stability of parasitical loop[J]. Acta Armamentarii,2011,32 (1):28 -32. (in Chinese)
[10] Masten M K. Applications of control theory to design of line-ofsight stabilization system[C]∥American Control Conference.Boston,MA:IEEE,1985:1219 -1222. .
[11] Lin C L,Hsiao Y H. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop[J]. IEEE Transactions on Control Systems Technology,2001,9(1):108 -121.
[12] Chu Z Y,Sun F C,Cui J. Disturbance observer-based robust control of free-floating space manipulators[J]. IEEE Systems Journal,2008,2(1):114 -119.
[13] Chladny R R.,Koch C R. Flatness-based tracking of an electromechanical variable valve timing actuator with disturbance observer feedforward compensation[J]. IEEE Transactions on Control System Technology,2008,16(4):652 -663.
[14] Yang Z J,Tsubakihara H,Kanae S,et al. A novel robust nonlinear motion controller with disturbance observer[J]. IEEE Transactions on Control Systems Technology,2008,16 (1):137 -147.
[15] Nesline F W,Zarchan P. Radome induced miss distance in aerodynamically controlled homing missiles,AIAA 84-1845[R]. Reston ,VA:AIAA,1984.
[16] Dwivdi P N,Tiwari S N,Bhattacharya A. A ZEM based effective integrated estimation and guidance of interceptors in terminal phase[C]∥AIAA Conference on Guidance,Navigation ,and Control. Toronto,Ontario Canada:AIAA,2010:6669 -6693.
[17] Zarchan P. Tactical and strategic missile guidance[M]. 5th ed.Virginia:American Institute of Aeronautics and Astronautics Inc,2007.
[18] 蔡毅. 光电精确制导武器[M]. 北京:兵器工业出版社,2013.CAI Yi. Photoelectric precision guided weapon[M]. Beijing:Publishing House of Ordnance Industry,2013.(in Chinese)
