龙门式机床横梁结构有限元模态分析

张东生，宁 玮，宋春明，张政武，余清华

大型龙门式数控机床是能源、航空航天、船舶、汽车、铁路、工程机械等行业不可缺少的重要加工设备，有加工跨距大、加工效率高、刚度高等特点。其中横梁作为龙门式机床的主要工作部件之一，起着连接滑座、滑鞍等关键部件的作用，其动态特性直接影响机床的加工精度和使用性能。龙门式机床工作时受各种激励作用，如设计不当，可能造成激励频率与机床横梁的固有频率相吻合，从而产生共振，影响机床的加工精度。因此，基于有限元法对龙门式机床的横梁进行模态分析，得到其动态特性，具有重要的意义。

国内外在机床研究方法上主要采用有限元分析方法，对结构动刚度和动态稳定性进行研究和评估［1－4］。机床横梁对于加工精度的重要性也得到研究人员的重视，文献［5］～［8］对机床横梁的设计和优化进行了研究，但对机床横梁进行动态分析尚存不足。因此有必要进一步对机床横梁的动态特性进行分析。

1 模态分析理论

模态是结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。结构的模态参数可通过模态分析获得，主要包括结构的固有频率和模态振型。如果获得了龙门式机床横梁的固有频率和结构模态，便可以设计和改进结构的动态特性，如避免产生激励源相关的共振现象，还可以了解机床横梁结构的整体刚度分布情况。

根据模态分析理论，结构上各点在激励下的响应，可表示成不同特定固有频率、阻尼比和振型等模态参数构成的各阶模态振型叠加，其动力学基本方程为:

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;x为位移向量;F(t)为激振力向量。

当F(t)=0时，忽略阻尼的影响，方程变为无阻尼系统自由振动方程:

自由振动时，结构上各点作简谐振动，各节点位移为:

将式(3)代入式(2)，可得:

式(2)的特征方程为:

式中:φ为特征向量，用于描述结构的振型;ω2为特征值，把第i个特征值的算术平方根ωi称为第i阶固有频率，其取决于结构本身的刚度、质量等参数。结构固有频率高，说明单位质量的刚度高。

2 龙门式机床横梁分析模型的建立

有限元计算的准确性依赖正确有效的有限元模型的建立。有限元模型需反映龙门式机床横梁的实际结构，根据横梁所受载荷的特点，横梁的内部结构通常设计为板筋形式，通过合理布置加强筋可以显著提高横梁的局部刚度。

在不影响计算精度的前提下，对结构做适当的简化，有利于提高计算效率。简化原则如下:

a.忽略结构焊缝和倒角。

b.对零件的外形进行必要的简化，忽略工艺孔和螺纹孔。

严格按照图纸尺寸，利用三维建模软件Pro/E建立龙门式机床横梁几何模型，如图1所示。

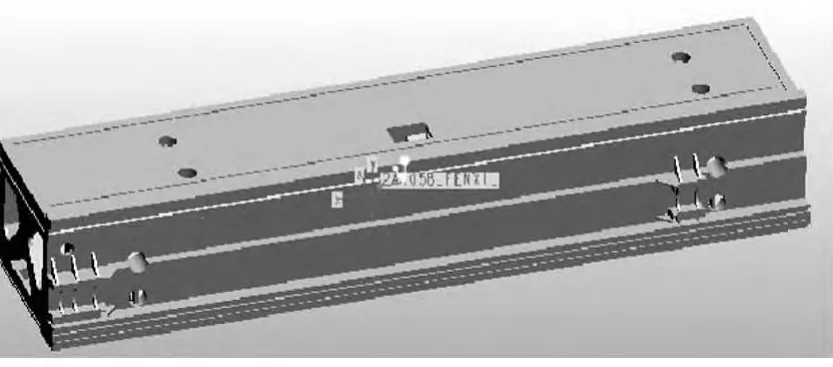
图1 横梁3D结构

把Pro/E软件中完成的龙门式机床横梁实体模型导入到ANSYS软件中进行有限元模型的建立。在有限元分析软件ANSYSWorkbench 12.0应用平台的环境下导入模型，导入的模型坐标系为系统默认的坐标系。选择AWE(ANSYS Workbench Environment)中的Simulation模块，有限元模型的材料参数设置见表1。

表1 横梁材料参数

利用ANSYS软件自动网格划分功能进行模型网格划分，得到三角形网格模型，节点数为109 226个，网格单元数为59 116个。

根据结构工作状态，在约束边界条件下研究龙门式机床横梁的结构动态特性。根据机床的结构，横梁部分的两端可以看成完全约束，约束施加在横梁表面两端突起的平面上。

3 横梁约束状态模态计算和分析

ANSYS具有强大的模态分析能力，提供7种模态提取方法，包括Block Lanczos法、Subspace法(子空间法)、Reduced法(缩减法)等。横梁有限元模型建立后，利用Block Lanczos法进行横梁约束边界条件下的模态计算。Block Lanczos法是求解大型矩阵特征问题的一种最有效方法，与子空间迭代法相比，该方法既具备多自由度大规模求解问题能力，又具有较高的求解效率，对模型单元的质量要求也不高，求解所需的计算机内存及硬盘空间也较低。与Reduced法相比，计算精度更优。

利用Block Lanczos法进行模态计算，提取结构的前四阶模态，横梁约束边界条件下的模态频率和振型见表2。

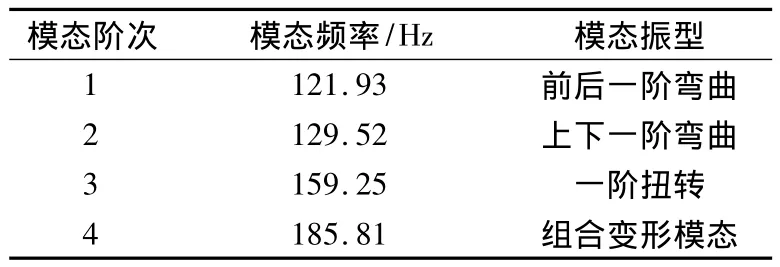
表2 横梁模态频率和振型

结构的振动变形通常可表示为各阶振型的叠加，横梁的振动主要由低阶振型组成，因此可忽略高阶模态的影响。

图2为龙门式机床横梁的一阶振型，模态频率为121.93Hz。一阶振型表现为机床横梁的前后结构整体变形，中部变形较大，为前后一阶弯曲变形。横梁的第一阶模态频率表明结构具有较好的刚度。

图2 横梁的一阶振型(频率121.93Hz)

图3 为机床横梁的二阶振型，模态频率为129.52Hz。二阶振型表现为机床横梁的上下结构整体变形，中部变形较大，为上下一阶弯曲变形。

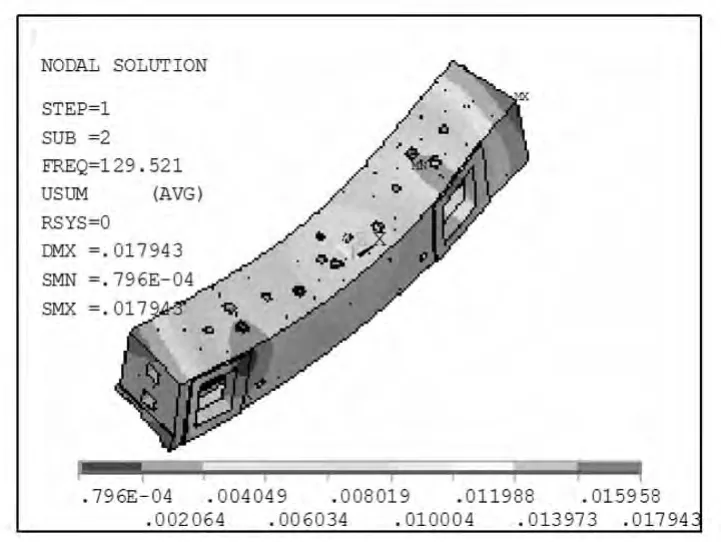
图3 横梁的二阶振型(频率129.52Hz)

对比图2和图3可知，由于第一阶振型为横梁前后一阶弯曲，第二阶振型为横梁上下一阶弯曲，通常刚度较弱的模态为低阶模态，因此横梁纵向弯曲刚度优于横向弯曲刚度。

图4为机床横梁的三阶振型，模态频率为159.25Hz。第三阶振型为绕梁轴向几何中心的扭转，横梁中部的扭转变形最大。

图4 横梁的三阶振型(频率159.25Hz)

由于扭转模态相对于横梁上下、前后一阶弯曲模态来说，模态频率更高，表明横梁结构具有较好的抗扭刚度，符合龙门式机床横梁高抗扭刚度的要求。

图5为机床横梁的四阶振型，模态频率为185.81Hz。第四阶振型为横梁结构的弯扭组合变形，最大变形在横梁中端下部。

图5 横梁的四阶振型(频率185.81Hz)

在进行结构设计时，应充分考虑机床的激励频率和横梁频率的关系，避免产生共振现象。龙门式机床的激励工作频率主要分布在0～60Hz范围内，横梁的前四阶固有频率均超过其工作激励频率，说明横梁的动态刚性好，在工作过程中，不会发生共振现象，且由加工过程引起的横梁受迫振动能够快速地衰减，从而保证机床的加工精度。

在设计机床横梁结构件时，通常强度不是主要考虑因素，达到高刚度才是主要的。因此，在龙门式机床横梁结构的设计中，在满足强度和刚度的条件下应尽可能地减轻龙门式机床横梁的结构质量。

4 结束语

通过对龙门式机床横梁进行简化，建立横梁的有限元模型，获得其结构固有频率和振型。研究结果表明，该机床横梁纵向弯曲刚度优于横向弯曲刚度，符合横梁载荷受力要求及设计要求，且龙门机床横梁的固有频率超过机床工作的激励工作频率，可以避免机床工作过程中横梁与激励产生共振，说明机床横梁具有良好的动态特性，保证了机床的加工高精度要求。因此，在研究结果基础上，可进一步展开龙门机床横梁动刚度结构优化和模态试验等相关工作。利用ANSYS对龙门机床的横梁进行了模态分析，获得横梁结构的前四阶模态频率和振型，说明利用有限元方法进行机床结构动刚度评估，是一种可靠的结构动刚度评价方法，可以实现有效降低产品开发成本，缩短产品开发周期的目的。

［1］ 关英俊，母德强，赵扬.GMCU2060龙门加工中心横梁结构有限元分析［J］.机床与液压，2011(11):131 －134.

［2］ 王一江，张晓艳，庞学慧.基于ANSYS的龙门铣床龙门结构模态分析［J］.机械，2010(4):49－50.

［3］ 张宪栋，徐燕申.基于FEM的数控机床结构部件静动态设计［J］.机械设计，2002(5):46－48.

［4］ 黄秋波，孙艳平，张德臣.立车横梁与工作台的有限元分析计算［J］.工艺与装备，2005(8):82－84.

［5］ 罗传林，李锻能.龙门式机床横梁的结构设计研究［J］.机电工程技术，2006(3):45－47.

［6］ 周乐，袁军堂，汪振华.龙门式机床横梁筋板结构分析与优化［J］.机械设计与制造，2014(1):15－17.

［7］ 王艳青，仲高艳，常永标.大型五轴联动加工中心横梁结构设计［J］.机床与液压，2012(13):114－117.

［8］ 王晓煜，贾振元，杨帆.龙门加工中心横梁部件的拓扑优化设计与分析［J］.制造技术与机床，2009(11):64－68.