基于能量最优的局部优化光顺处理
2014-02-28司昆明樊留群赵建华
司昆明,樊留群,朱 蓓,赵建华
在数控加工中,粗加工时,为实现高速高效加工,需要对待加工的曲线曲面进行光顺处理;精加工时,为了得到较光滑的曲面,也要对CAD/CAM处理后拟合的曲线进行光顺处理。可见,光顺处理在数控加工中发挥着举足轻重的作用。
目前,针对曲线的光顺处理方法大致可以分为以下两类:选点修改法和优化法。选点修改法[1-2]指的是逐次找出造成不光顺的数据点(即“坏点”)并对其进行修正处理。而优化法则分为两种:整体优化法和局部优化法。整体优化法[3]一次对所有的型值点进行修正,可以起到很好的整体光顺作用,但其计算量过大,且操作速度较慢。局部优化法[4-6]则兼具选点修改法和整体优化法的优点,该方法不仅计算量小,而且整体光顺效果好。
在对“坏点”判定时,文献[1]、[7]仅从曲率的角度来考虑,这种判定“坏点”的方法在数控加工中是不合理的,会导致修正后的曲线越来越往直线的趋势发展。因此,本文提出一种同时考虑相邻弦间夹角和曲率的“坏点”判定方法。文献[8]~[10]仅对“坏点”的位置做了修正处理,却都没有对“坏点”处的切向量进行修改。一般如果控制点的位置有问题,那么它所对应的切向量也应该进行修正处理。针对以上情况,本文提出了针对“坏点”的位矢和切矢同时进行修正处理的局部光顺算法。
1 “坏点”的判定
已知型值点列为 Qi(i=0,1,2,…,n),设Q(t)是插值于{Qi}的非均匀三次样条曲线,ki是样条曲线Q(t)在型值点Qi处的相对曲率。为满足曲线光顺性的要求,选点修改法一般分两个步骤进行,即粗光顺和精光顺两个阶段。
1.1 粗光顺阶段“坏点”的判定
在粗光顺阶段,通常按以下方法判定“坏点”[7]:
a.相对曲率的符号序列{sign(ki)}中连续变号的点,即但凡满足条件

成立的型值点Qi称为“潜在坏点”。
b.对于已知的样条曲线,设允许的相邻弦间夹角的最小值为θmin,Qi点与相邻的两个型值点Qi-1,Qi+1构成的弦夹角记为 θi,若 θi< θmin且满足式(1),则称点 Qi为“坏点”。
c.由于在同一条曲线上存在出现多个“坏点”的可能,为减少工作量并获得理想的光顺效果,首先应找出“坏点”中的“最坏点”进行修正。此处令

1.2 精光顺阶段“坏点”的判定
在精光顺阶段,通常将ki的一阶差分符号序列{sign(Δki)}中连续变号的点,即满足条件

成立的点称作“坏点”。同时,令
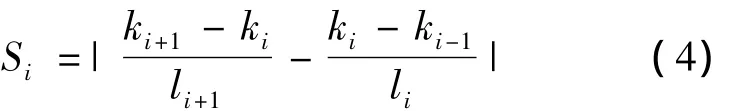
式中:li= ‖Qi- Qi-1‖,为弦长;Si为曲线 Q(t)在点Qi处的剪力跃度。在精光顺阶段,把剪力跃度最大处的点Qi称为“最坏点”。
2 “坏点”的修正
2.1 非均匀三次样条曲线
设插值于给定型值点Qi的参数三次非均匀样条曲线为:

根据条件

可求出

式中:Δi=ti+1-ti。
由于累加弦长参数化能够如实地反映出数据点弦长的分布情况,并一直被认为是最佳参数化法,因此本文采用累加弦长参数化,即
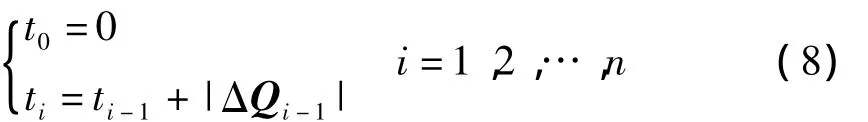
式中:ΔQi-1=Qi- Qi-1,为向前差分矢量,即弦线矢量。
2.2 基于能量最优的光顺算法
样条曲线的应变能为 E=C∫(Q″(t))2d t,其中C为与样条刚度有关的系数。记光顺前后样条曲线的应变能分别为E和E*,光顺前后样条曲线的应变能的变化量记ΔE。可求得
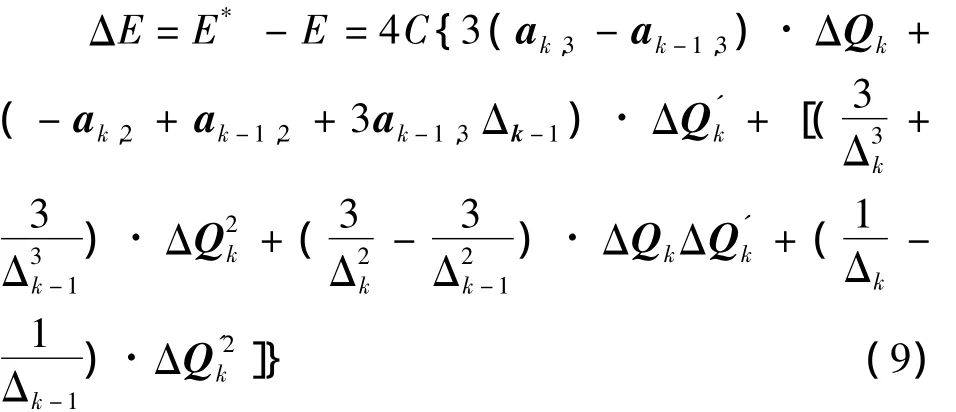
式中:Δk=tk+1-tk。要使得光顺后的应变能最小,将式(9)分别对 ΔQk和 ΔQ'k求偏导,并令偏导分别为零,即

带入数值,求得:

最后,将“坏点”的位置矢量和切矢分别修正为:

使用该种方法对“坏点”进行修正时,要考虑一种情况:位矢修正量ΔQk大到一定程度,而超出数控加工时所允许的误差公差带。在纯粹进行曲线光顺处理时该种情况可以不加考虑,但在数控加工时,该类情况却不容忽视。否则,会在提高工件光滑性的同时降低加工精度。因此,在保证加工精度的前提下,为使得数控加工出的工件尽可能光滑,本文引入位矢最大允许修正量ΔQmax,其值由数控加工时允许的误差公差带决定。当ΔQk≥ΔQmax时,令ΔQk=ΔQmax。这样处理虽会使得样条曲线的光顺性较引入ΔQmax之前有所降低,却能在保证加工工件精度的前提下,尽可能使加工出的工件光滑。
2.3 “坏点”修正的流程
步骤1,过型值点构造三次非均匀样条插值曲线C0(t)。
步骤2,按照能量最优原则分别将“坏点”的位矢和切矢分别修正为Q*k和。
步骤3,若“坏点”位矢修正量ΔQk大于最大允许修正量 ΔQmax,则取 ΔQk=ΔQmax,而切矢修正大小仍取ΔQ'k。
步骤4,对修正后的型值点重新进行样条插值,若仍旧有“坏点”则继续按照以上步骤进行修正,反之,输出得到修改后的参数样条曲线C(t)。
光顺处理流程如图1所示。
3 仿真验证
下面通过一组算例来验证本算法的有效性。选取如表1所示的实验数据点,对表中的数据点进行三次非均匀样条曲线拟合,设定允许的相邻弦间夹角的最小值 θmin为45°,允许的最大修正量ΔQmax设为0.5(单位量纲为1)。找出造成样条曲线不光顺的点,并按本文介绍的“坏点”修正方法进行光顺处理。经MATLAB仿真得出光顺前后的4幅图,其中,图2和图3分别表示光顺处理前后的样条曲线;图4和5分别表示光顺处理前后的样条曲线曲率。通过对比可看出采用本文算法对原拟合曲线进行光顺处理后,曲线的斜率更均匀了,曲线也比原来光滑了,从而验证了本文算法的有效性。

表1 选取的数据点列

图2 光顺前的曲线

图3 光顺后的曲线
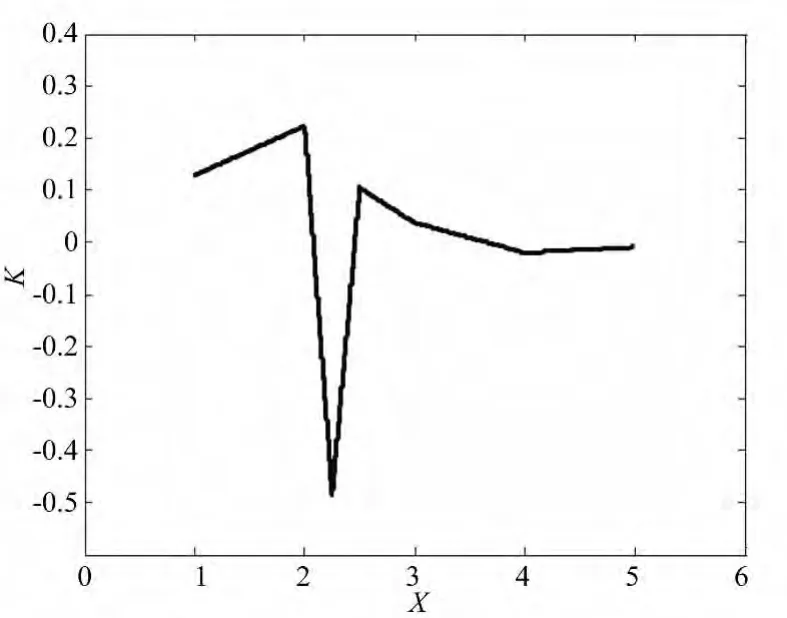
图4 光顺前的曲线曲率
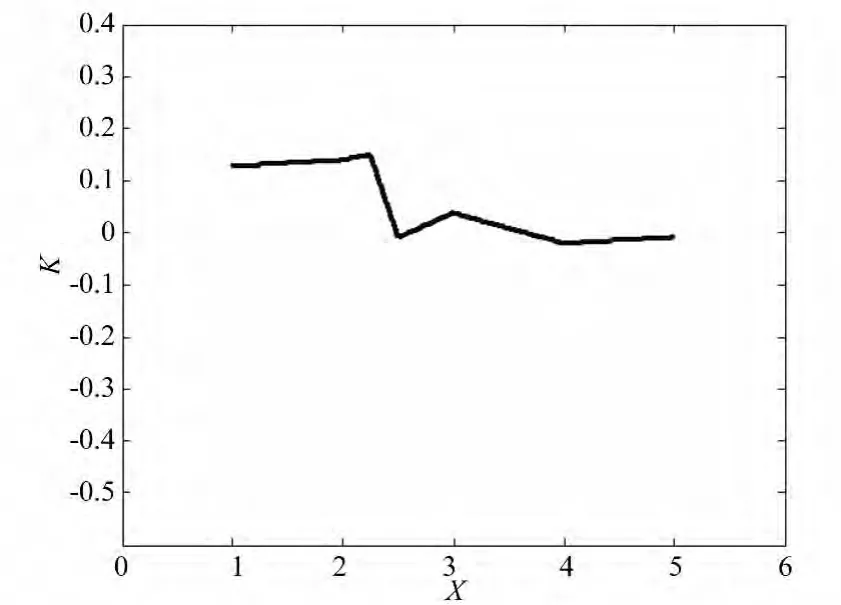
图5 光顺后的曲线曲率
4 结束语
本文在国内外学者研究的基础上,提出在判定不光顺点时同时考虑相邻弦间夹角和曲率因素的“坏点”判别方法。另外,在处理这些不光顺点时,本文采用基于能量最优的局部光顺算法对“坏点”位矢和切矢同时进行修正处理。仿真实验表明,通过该算法进行处理后,曲线的曲率更均匀了,曲线也更光顺了。
[1] Kjellander J A P.Smooting of cubic parametric spline[J].CAD,1983,15(3):175- 179.
[2] Farin G,Rein G,Sapidis N,et al.Fairing of cubic B-spline curves[J].CAGD,1987,12(4):91~103.
[3] Poliakoff JF.An improved algorithm for automatic fairing of nonuniform parametric cubic splines[J].Computer- Aided Design,1996,28(1):59-66.
[4] 龙小平.局部能量最优法与曲线曲面的光顺[J].计算机辅助设计与图形学学报,2002,14(12):1109-1113.
[5] 王远军,沈燕南.五次参数样条曲线的能量最优光顺算法[C]//第二届全国几何设计与计算学术会议论文集.合肥:中国科学技术大学出版社,2005:203-206.
[6] 穆国旺,宋秀琴,臧婷.一种选点法和能量法相结合的曲线光顺方法[J].工程图学学报,2005,22(6):118-121.
[7] 罗青.数控代码光顺处理方法研究[D].广州:广东工业大学,2007.
[8] 郑兴国,朱婉婕,夏成林,等.带形状参数控制的三次B样条曲线曲面的光顺[J].大学数学,2012,28(4):87-91.
[9] 章虎冬.一种参数三次样条曲线光顺优化算法[J].工程图学学报,2011,17(3):41 -44.
[10]罗卫兰,杨勋年,郑建民.B样条曲线的约束光顺算法[J].浙江大学学报,2004,31(1):51 -57.
