基于随机振动分析的隔振支架结构优化研究

唐 波

(重庆工业职业技术学院，重庆 401120)

0 引 言

振动与冲击是导致的电子装备故障破坏的主要形式。隔振支架是复杂随机激励环境下保障关键电子装备正常工作的重要支撑及减振缓冲结构。将动态载荷化为静载的传统静态设计方法，已经不能满足当前隔振支架结构的工程设计需要。国内外学者对在结构动力优化设计方面进行了相应的研究[1-8]，取得了一定的研究成果。陈施能[1]以某型航空电子设备及其安装架为研究对象，利用有限元方法对航空电子设备及安装架进行静态强度分析及动力学分析，并对安装架进行了优化设计。刘范川，等[2]对机载电子设备减振系统的固有特性进行研究，并通过工程实例进行了验证。张军，等[3]根据某配重卫星对隔振的要求，设计出了一种整星隔振器，并进行了考虑激励载荷下的动力学分析。任建峰[4]利用瞬态分析及随机振动分析理论对电子设备典型结构及其装配连接进行了动力响应行为的分析和研究。

笔者将有限元方法、动力学模态分析技术与随机振动理论相结合，考虑关键电子装备的实际随机激励，建立了隔振支架结构系统动力学模型，在随机振动分析的基础上进行了支架结构优化设计研究。

1 隔振支架动力学有限元模型

采用现代机械设计软件CATIA对隔振支架结构进行三维结构设计，如图1。支架架构主要由支脚，主支撑平台和主挡块构成。

图1 支架结构模型Fig.1 Support structure model

通过频响函数计算可以得到随机激励振动响应的统计特性。设在激励X(ω)=ejωt下，系统响应为Y(ω)。采用有限单元法对支架结构进行离散，单位复谐和激励的单自由度系统振动方程为：

(1)

系统频率响应函数为：

(2)

多自由度系统频响函数矩阵为对角阵：

[H(ω)]=diag[Hk(ω)]，(k=1,2,3,…,n)

(3)

响应的均值列阵为：

(4)

对支架结构模型进行合理简化处理，去掉不影响结构刚度的小倒角、小圆弧、小圆孔、小凸台等。采用四面体实体单元对支架进行有限元网格划分，共计252 236个单元，得到其有限元模型如图2。

图2 支架结构网格模型Fig.2 Mesh stent structure

2 支架结构动态响应分析

实际工作时，隔振支架结构振动环境加速度功率谱从20～2 000 Hz，如图3，属于典型宽带随机功率谱。采用Lanczos算法求解约束条件下支架结构前10阶固有频率及前6阶振型，如表1及图4。

图3 振动功率谱密度函数Fig.3 Vibration power spectral density function

阶数频率阶数频率1617.761132.22698.471390.031026.881403.241049.191556.551071.9102294.3

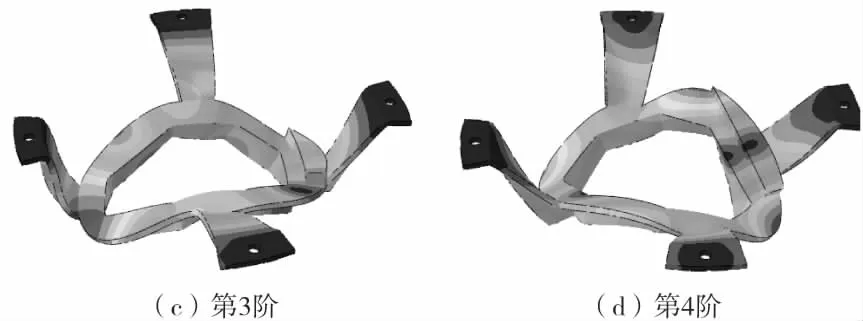
图4 支架结构前6阶计算模态振型Fig.4 6 order to calculate the structure ofthe front bracket modal shape

应用有限元程序ABAQUS的随机响应分析模块，对模型施加功率谱密度得到支架结构垂直安装面z方向的均方根应力分布,如图5。

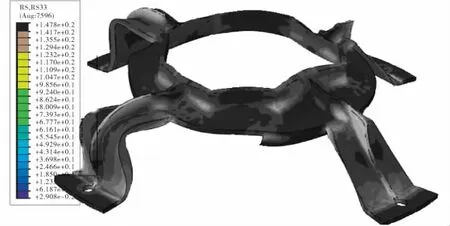
图5 支架结构均方根应力分布Fig.5 RMS stress distribution of support structure

支架结构z向均方根主要分布在支架结构侧翼肋板处，整个结构应力分布均匀，满足材料正常许用要求。由于支架实际工作时，精密电子仪器安装于隔振支架中间主支撑平面，因此支撑平面各节点的振动响应直接影响电子设备的振动情况。选择主支撑平面的四个对称位置2 455，2 549，13 032，22 014节点响应值进行分析，如图6。

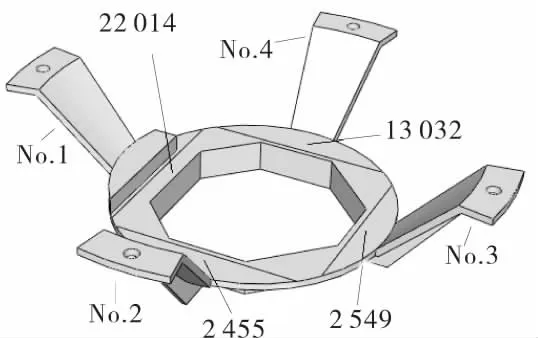
图6 关键节点位置Fig.6 Key node location map

提取2 455，2 549，13 032，22 014节点加速度响应均方根值,如表2。从中可以得出结构振动响应靠近挡块位置高于其他位置，且主要以z向为主。

表2 支架结构加速度响应均方根值

提取挡块处22 014节点x,y,z方向位移响应谱线,如图7。从图7中可以看出，支架结构位移响应谱上具有多个峰值，这些峰值频率主要集中分布在支架结构的自身固有频率处，说明振动响应的能量集中分布在支架结构的自身固有频率处。提取各节点位移均方根值，如图8。

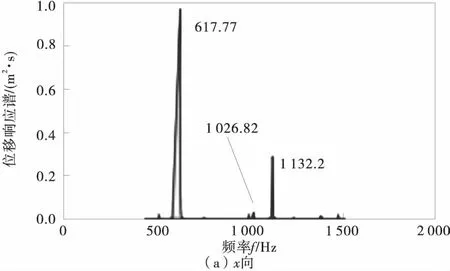
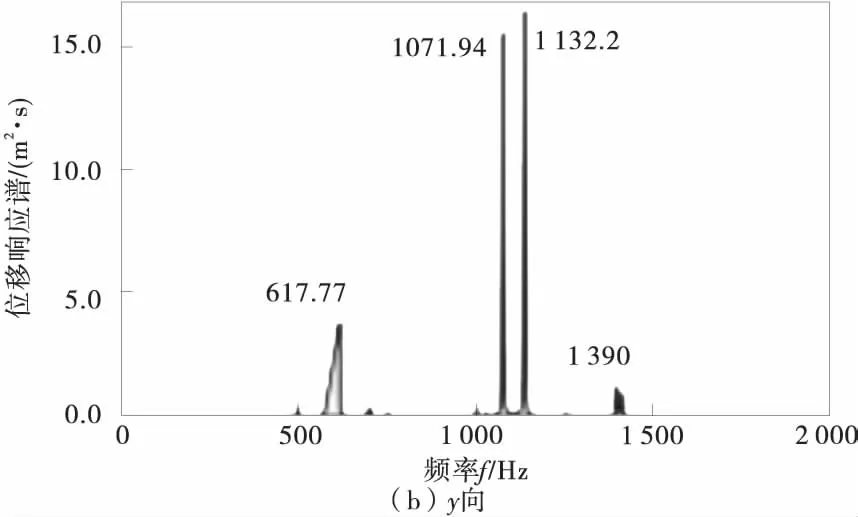
图7 22 014节点位移响应谱线Fig.7 22 014 nodal displacement response spectrum

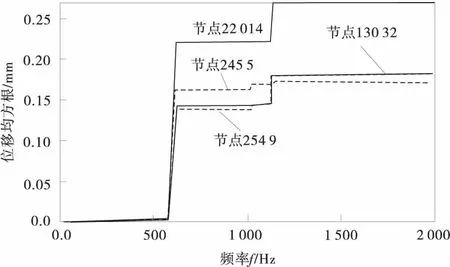
图8 关键节点位移均方根值Fig.8 The key nodal displacement RMS

1号支脚位移均方根响应明显高于2、3和4号支脚，支架结构在571.3 Hz开始，系统振动能量明显增加，到617.7 Hz左右达到一个相对稳定水平，1 132 Hz处振动能量明显增大，各节点间振动能量差值较大，因此需要对隔振支架结构进行优化改进。

3 支架结构优化与动力学重分析

隔振支架优化设计的目标是在保障对精密电子装备足够支撑强度与刚度条件下，减少结构重量、使隔振支架结构上电子装备主支撑平面响应应力和位移幅值降低、并使其尽量均匀，减少应力集中。具体结构优化措施为：4个支脚板厚减薄1.5 mm，支撑平台板厚减薄3 mm，安装主挡块高度降低14 mm，添加主档快对侧的辅挡块。同时由于原结构应力集中发生在支脚与支撑平台的连接处，改进设计时添加R15 mm的圆角，优化设计后的支架结构见图9，结构重量实现减重21.8%。

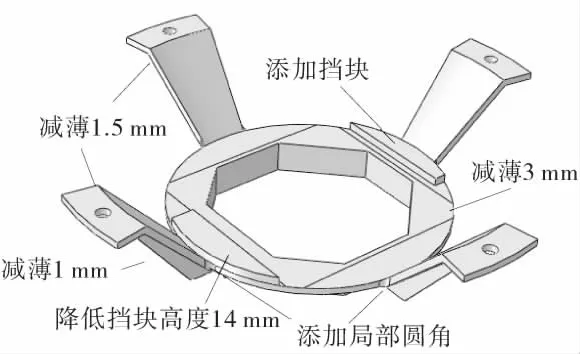
图9 支架结构优化改进简图Fig.9 Optimized and improved support structure diagram

对改进的支架结构进行动力学重计算，得到前10阶固有频率，如表3。

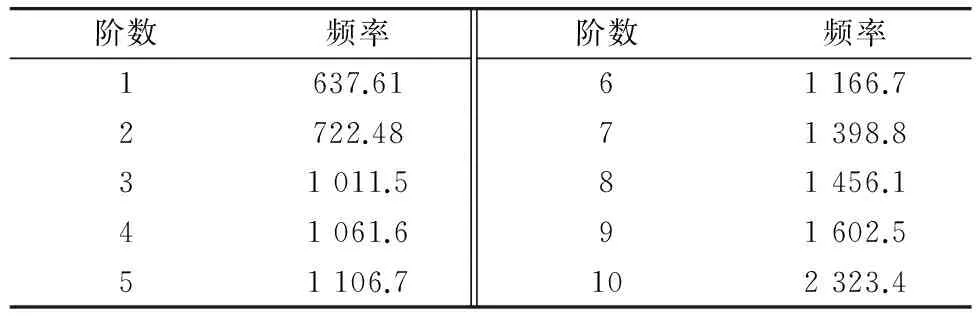
表3 优化后支架结构前20阶固有频率

优化后支架结构受到随机激励后其z方向的均方根应力分布如图10。可以看出结构z向最大均方根应力由147.8 MPa降低为122.8 MPa，且整体分布更加均匀。

图10 优化后支架结构均方根应力分布Fig.10 RMS support structure stress distribution after optimization

优化前后提取支架安装面相同位置22 014节点的位移对比响应频谱线，如图11。优化后支架位移响应幅值较原结构响应幅值降低幅度为12.7%，且主要响应频率由1 132.2 Hz转移到1 166.7 Hz，为优化后支架结构第6阶固有频率。提取22 014节点优化前后位移均方根谱线，如图12。

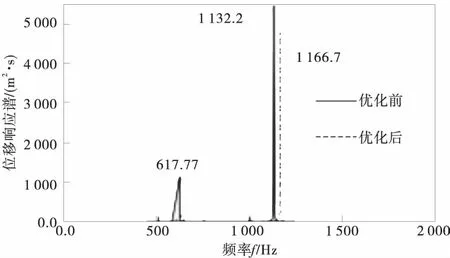
图11 优化前后支架结构22 014节点位移响应谱Fig.11 Support structure 22 014 node displacement responsespectra before and after optimization

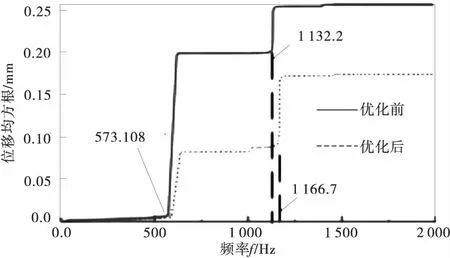
图12 优化前后支架22 014节点位移均方根谱线Fig.12 Around 22 014 nodes to optimize stent displacement RMS line

从图中可以看出，优化后支架结构22 014节点位移均方根响应主要集中在结构第6阶固有频率处，且幅值明显小于原结构，振动能量明显降低，减少幅度达到32%。综上，优化后支架结构各阶固有频率较优化前有所增加，随机激励下响应应力、位移值降低且分布更加均匀，满足使用要求。

4 结 语

将有限元理论，动力学，模态分析理论及随机振动理论结合起来，建立支架结构动力学有限元分析模型，基于随机振动响应分析，在满足支架承载强度与刚度的条件下，对支架进行了结构优化。优化后支架结构各阶固有频率有所提高，系统刚度增强，同时实现了支架结构的轻量化设计，在保证足够强度及刚度的前提下整体减重21.8%，随机激励下支架结构响应应力、位移值降低且分布更加均匀，有效的避免了支脚与主支撑平台连接部位的应力集中，优化后支架结构关键节点激励方向位移均方根响应主要集中在结构第6阶固有频率处，幅值明显小于原结构，振动能量减少32%，结构设计更加合理，研究具有一定的理论意义与工程价值。

[1] 陈施能.某型航空电子设备及安装架动力学分析[D].成都:电子科技大学,2007.

Chen Shineng.Dynamic Analysis for the Bracket of the Electronics Equipments and Aircraft[D].Chengdu:University of Electronic Science and Technology of China,2007.

[2] 刘范川,任建锋,刘世刚.机载电子设备隔振系统固有频率的确定[J].电讯技术,2007,47(3):195-198.

Liu Fanchuan,Ren Jianfeng,Liu Shigang.Determining the free frequency of vibration isolation system for airborne electronic equipment[J].Telecommunication Engineering,2007,47(3):195-198.

[3] 张军,谌勇,张志谊,等.整星隔振器的隔振性能分析[J].宇航学报,2005,26(增刊1):110-113.

Zhang Jun,Chen Yong,Zhang Zhiyi,et al.Performance analysis of the whole-spacecraft isolator[J].Journal of Astronautics,2005,26(S1):110-113.

[4] 任建峰.电子设备结构动力响应研究中的关键技术[D].西安:电子科技大学,2006.

Ren Jianfeng.Key Techniques in the Research on the Dynamic Responses of the Electronic Equipments[D].Xi’an:University of Electronic Science and Technology of China,2006.

[5] 刘衍平,高新霞,张刘斗.电子设备机柜随机振动试验的数值模拟[J].塑性工程学报,2007,14(4):151-155.

Liu Yanping,Gao Xinxia,Zhang Liudou.Numerical simulation tested to electronic equipment cabinet random vibrations[J].Journal of Plasticity Engineering,2007,14(4):151-155.

[6] Zarghamee M S.Optimum frequency of structures[J].AIAA Journal,1968,6(4):749-750.

[7] Pantelides C P,Tzan S R.Optimal design of dynamically constrained structures [J].Computers & Structures,1997,62(1):141-149.

[8] Tizzi S.A Ritz procedure for optimization of cylindrical shells,formed by a nearly symmetric and balanced angle-ply composite laminate,with fixed minimum frequency [J].Computers and Structures,2006,84(31):2159-2173.