基于安全和时间的广义路阻模型建立

孔令总，柳本民，周小焕，李志中

(1.同济大学 道路与交通工程教育部重点实验室, 上海 201804；2. 云南省交通科学研究所，云南 昆明 650011)

重大自然灾害发生后，其影响范围区域内随即进入了紧急状态，应急救援指挥中心会在灾区公路网中选择最优救援路径，以便救援队伍能够安全快速的进入灾区进行救援。以往救援指挥中心对灾后最优路径的判断往往是根据经验得出[1]。因此，确定紧急情况下动态路网最优路径的选择模型，实现对应急救援车辆有效的交通指导是十分必要。

目前常用的最优路径选择模型都是针对常态交通流，紧急情况下的最优路径选择模型很少。在常态交通流情况下，路网不会发生变化，以致常态交通流诱导模型仅考虑了交通需求的变化，而没有考虑路网的变化。然而在紧急情况下，由于突发事件的破坏作用，道路条件、交通条件都发生了变化，仅考虑交通条件变化的常态最优路径选择模型不适用于紧急情况下。因此，对常规最优路径模型进行了改进，首先分析紧急情况下路网特性，结合路网变化后对行车安全造成的影响，引入路网安全性指标，再结合时间指标建立广义路阻函数，以算路段的路组；再通过Dijkstra算法，建立基于时间和安全性紧急情况下最优路径选择模型；最后通过云南盈江“3.10”地震的救援实例对模型进行验证。

1 广义路阻模型

重大灾害发生后，灾区范围内的道路网会发生巨大的变化，其中路面条件、道路设施、管理水平等都会有很大的变化，潜在次生灾害也会对路网产生不确定性的影响。路网处于动态变化的状态，直接影响到路网上车辆行驶的安全性。因此，灾后应急救援路径选择时，同时考虑安全性和时间因素的路阻模型比单纯的从时间因素考虑的路阻模型，更加有实际意义，所以笔者建立了基于安全性和时间因素的广义路阻模型。

1.1 模型建立

所谓公路网广义路阻，是指在人-车-路这3方面因素下出行者为了完成从出发点到目的地而受到的阻力总和。在应急救援中影响广义路阻最重要的两个因素是车辆行途中花费的时间和救援队伍的安全性。所以，在建立模型时包含了路段行驶时间T、路段安全性指数C两种路阻在内的广义路阻函数F[2]，见式(1)：

F=α1T+α2C

(1)

式中：α1，α2为路阻的非负权重系数。

考虑到公路网的复杂性，救援车辆在公路网某两个OD点间的某条救援路径可能由若干个技术等级、路面类型、路况破坏程度等因素不同的路段构成，因此，在计算路径广义路阻的时候要分段计算，以便参与最优路径分析。若公路网中某两个OD点，如(m,n)间有i条路径，其中第i条可行路径由ji段路段构成，则(m,n)间第i条路径的广义路阻函数为Fi(m,n)，见式(2)：

(2)

1.2 指标确定

当重大自然灾害发生时，由于道路功能损失、余灾、信息滞后性等不确定因素的存在，公路网处在一个复杂的动态变化公路交通系统中。为了更精确的确定道路路阻，需要分别对路阻指标进行量化。

1.2.1 时间指标确定

路段行程时间是指应急救援车辆从出发点到目的地行驶的时间。实际计算中路段行程时间可以用路段平均行程时间来代替。由交通工程学理论可知，路段平均行程时间可用式(3)计算[3]：

TP=ε·L/VP

(3)

式中：TP为路段平均行程时间，h；ε为公路功能损失调整系数；L为路段距离，km；VP为路段平均行程速度，km/h。

不同等级的灾害类型对道路的破坏情况不同，导致道路行车状况不同，因此引入道路功能损失调整系数ε(表1)。ε的数值是通过选取不同技术等级的标准路段比较对象，然后选取不同路况下的路段作为被比较对象，通过行车试验，由标准路段车速与实验路段车速之比而确定的取值范围。马永锋[4]针对国内公路交通实际状况,在进行了大量公路网速度、流量等相关数据调查分析后,结合我国大规模的实际交通调查数据，在美国联邦公路局的交通阻抗模型基础上，对不同的道路等级进行了模型参数标定,给出了车速-流量通用模型〔式(4)〕，标定的模型参数取值见表2。

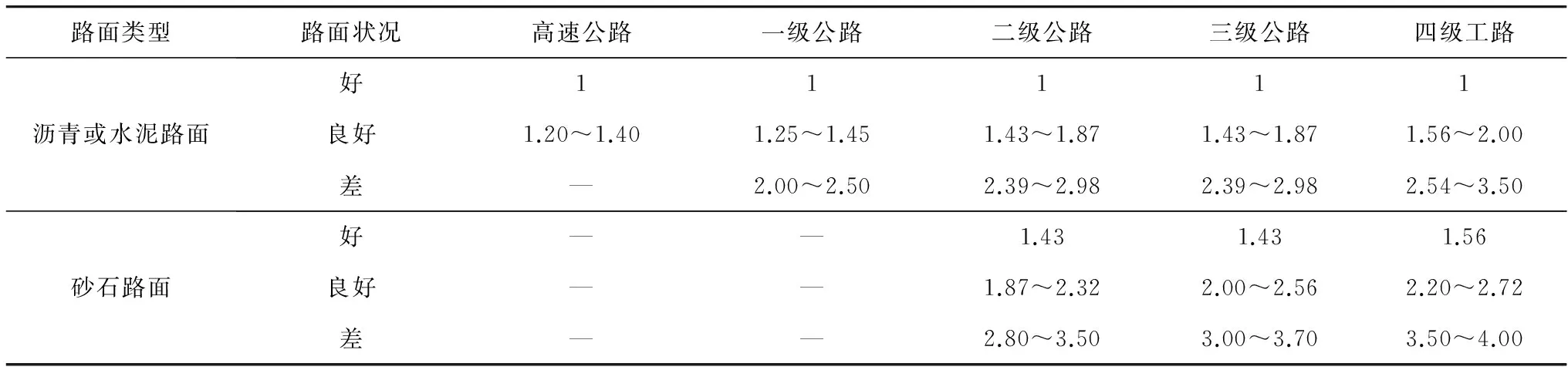
表1 道路功能损失调整系数

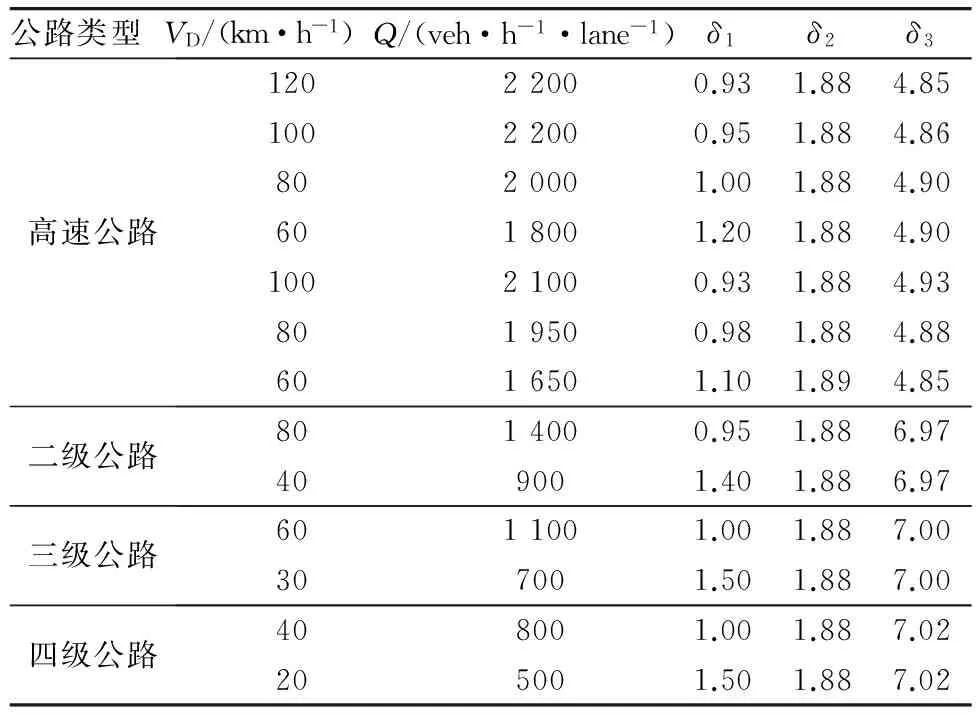
表2 车速-流量通用模型参数

(4)

式中：VP为路段平均行驶车速，km/h；VD为各级公路设计车速，km/h；Q为公路单车道交通量，veh/(h·lane)；q为公路单车道实际通行能力,veh/(h·lane)；δ1，δ2，δ3为回归系数；γ为修正系数。

1.2.2 道路可靠度参数确定

路段可靠度是指应急事件发生后，在一定的道路路况和管理条件下，道路交通系统在当时保持正常安全运行的能力。道路可靠性的研究是根据外界环境事件对其通行安全性的影响进行事件分级，并确定各级事件下元件可靠度的折减系数，以此来判断外界环境事件对其可靠度的影响。结合灾变事件分类分级的方法，采取式(5)来确定道路可靠性参数[5]：

R=kijR0

(5)

式中：R0为正常运营条件或无灾变事件时系统元件的基本可靠度；R为具体灾变事件下系统元件的实际可靠度；kij为具体环境(或者环境事件)对系统元件可靠度的影响系数(i代表环境事件类型，j代表i环境事件类型下的具体级别)，kij的值目前主要采用专家评判法获取，当积累数据足够时应考虑结合统计资料进行修正。

1.2.3 安全性指数确定

路段安全性指数是指应急救援车辆能否安全到达目的地的定量指标值。路段安全性指数C的数值与灾害后路网的破坏程度有关，C=1/k，其中k为路段可靠度。

系统的整体可靠度由人-车-路3要素共同决定，在路径选择中，规定救援车辆的可靠度为1，3要素构成的道路交通系统的任一要素失效，系统就会失效，只有当3要素都能正常工作时，单元交通系统才能正常运行。因此，根据可靠性工程中串联系统的定义[6]，单元交通系统实质是各要素以串联方式连接的串联系统，由此得到路段可靠度的数学模型：

k=kr×km

(6)

式中：kr为道路可靠度；km为管理可靠度。

1)道路可靠度取值

道路的可靠度是由道路完整可靠度、路段速度差可靠度、次生灾害可靠度、道路等级可靠度共同决定的，其大小是4个因素的乘积。结合式(5)，采取专家评判法，此处给出各种不同级别的路况条件对司机可靠度的影响系数[5]，见表3。

表3 道路可靠度

(续表3)

项目标准可靠度道路等级高速0.999一级0.999二级0.999三级0.900四级0.900

2)管理可靠度取值

灾害条件下，对应急救援队伍的路径引导服务水平，主要体现在道路的管理可靠度上。管理可靠度作为道路交通系统的外部人为环境因素，分别通过信息提供可靠度、管理执法可靠度两方面分析对交通安全的影响。结合式(5)，采取专家评判法，此处给出各种不同级别的管理条件对司机可靠度的影响系数[5]，详见表4。

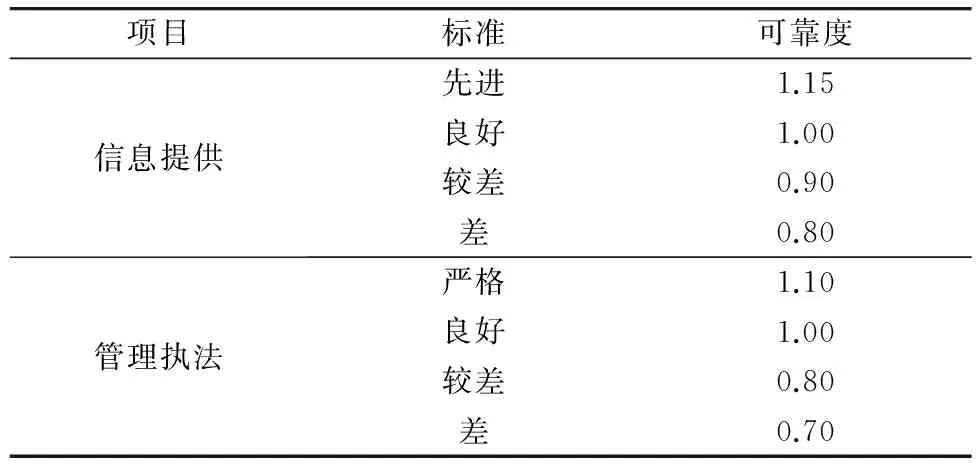
表4 管理可靠度

1.3 指标权重

确定权重的方法很多，有专家评分法、调查统计法、层次分析法、主成分分析法等，对于广义路阻模型中的时间和安全性这两个评价指标都跟路阻函数有明确的主观相关性，所以专家评分法更适合模型评价指标权重的确定。指标打分标准则直接以专家评分的形式给出评分值，评估标准分为5个等级，各等级的定性描述如图1。

图1 指标评估标准Fig.1 Evaluation criteria of indicator

通过不同领域的专家依据指标评估标准对影响广义路阻的两个因素分别进行打分，要求每位专家每次对行程时间和路段安全性两个指标的评分分数相加为100分。然后根据不同专家的权威性对评分数据进行加权平均，最后确定广义路阻模型权重：路段行程时间权重为0.35；路段安全性指数权重为0.65。

1.4 模型确定

1.4.1 指标标准化

由于路段的行驶时间与安全性指数两个指标之间的量纲不同，为了得出适用的广义路阻函数值F，需要对其进行标准化处理，见式(7)，通过处理将其映射到[0,100]范围内：

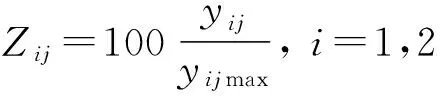
(7)

式中：yij表示第i个指标中的第j个实验值，yijmax=max{yij|j=1,2,…,n}；Zij为评价指标标准化后的处理值。

1.4.2 模型确定

通过建立基于安全性和时间因素的广义路阻模型，确定模型的评价指标和权重，最后对评价指标进行标准化处理，最终得出适用于应急救援的广义路阻模型：

F=0.35ZT+0.65ZC

(8)

式中:ZT为标准化后的行驶时间；ZC为标准化后的安全性指数。

2 最优路径选择方法

2.1 算法确定

救援车辆行驶的路径并非在起点就一次性的选择好救援的路径，而是在救援过程中每到一个交通结点(决策结点)都要做出选择，选择一条连接当前所在结点到下一个结点的最优路径，依此类推直至到救援目的地。当灾害发生后，由于诸多的不确定因素存在，道路网处于一个动态变化的状态，可见，实际的救援路径的选择是一个动态的过程。

基于上述分析，选择引用Dijkstra算法[7]作为灾害条件下最优路径选择方法，它是适合于所有路径均为非负的最优路径算法，是目前公认的求解最优路径问题的最经典的算法。

2.2 Dijkstra算法

Dijkstra算法适合路径的动态选择过程，它可以动态的给出从某指定顶点到图中所有顶点之间的最优路径[7]。要找出任意两地之间的最优路径，首先对地图中的所有路线抽象成路网无向图，然后建立一个邻接矩阵，它表示路网中任意两地间的邻接关系及其路阻(若两地间无连接关系，则其路阻值设为∞；若两地间有连接关系，则其路阻值通过文中广义路阻函数模型计算得到路阻)，最后把路阻带入Dijkstra算法中求得最优路径[8-10]。

3 实例分析

3.1 实例概况

盈江县地处云南省西南部，东北、东南、南面分别与腾冲、梁河、陇川3县相连，西、西北、西南与缅甸接壤。2011-03-10在云南盈江发生5.8级地震，此次地震造成公路桥梁不同程度受损，但是地震并没有造成交通中断，通往盈江的S233、S318、G56、G320、S317等主要干线公路基本能够通行。图2是通往盈江县的主要干线公路，本次救援车辆主要从保山市出发到达盈江县城，所以此次实验的目的是寻找保山市至盈江县的最优路径。盈江县的周边路网示意图见图3和路径基本信息见表5。

图2 盈江路网Fig.2 Road network of Yingjiang

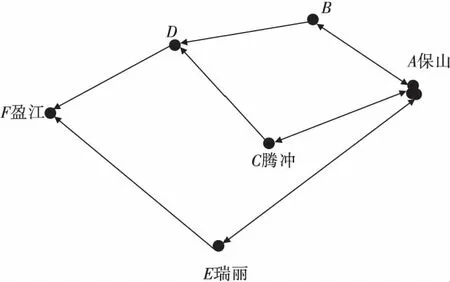
图3 路网示意Fig.3 Road network diagram

起始点路径连通性途经道路长度/km交通量/(pcu·h-1)限速值/(km·h-1)保山—腾冲A—B—D0.90.7G56杭瑞高速—S31723574003006040A—C—D0.90.8G320—S31750524003006040保山—瑞丽A—E0.9G32018140060腾冲—盈江D—F0.6S2338330040瑞丽—盈江E—F0.7S23310030040

3.2 确定最优路径

3.2.1 广义路阻的确定

1)由式(3)、式(4)、式(7)以及表1、表2中的数据可以算出各路段的标准化后的行驶时间ZT(表6)。

2)由式(6)、式(7)以及表3、表4中的数据可以算出各路段的标准化后的安全指数ZC(表6)。

3)由式(8)得到各路段广义路阻Fi的大小(表6)。

表6 路段路阻

3.2.2 确定最优路径

经过对盈江路网的提取和分析后，通过广义路阻模型得到路段的权重，再由Dijkstra算法求得A点(保山市)到其他各点的最短距离，A点到F点(盈江县)的最优路径为A—E—F。

3.2.3 最优路径的比较

由表6中的时间路阻可以得出只考虑单一时间因素时，得出的最优路径是A—B—D—F。然而在路径A—B—D—F中路段D—F段道路受到地震破坏比较大，对行车的安全有很大的隐患，不适合救援车辆通行。相反，路径A—E—F虽然行车时间比路径A—B—D—F略长，但是此路段总体上受到地震灾害的影响不大，救援车辆可以比较安全的到达目的地。经过综合分析A—E—F更加适合救援车辆通行。因此，基于安全和时间因素的广义路阻模型在实际应急救援时更加具有意义。

4 结 语

在现有的路阻函数模型的基础上，结合重大灾害条件下实际的道路通行状况，提出了基于行车安全和行驶时间的广义路阻模型，并通过查阅文献、实际调研、专家评分等方法确定了相关的参数和指标权重。最后结合具体实例，通过应用该模型求得的最优路径与传统路阻模型求得的最优路径作比较，结合具体情况论证了模型的实用性。

[1] 张海军,张珏,杨晓光.异常事件下高速道路交通状态的分析与仿真[J].交通运输工程学报,2008,8(2):116-121.

Zhang Haijun,Zhang Yu,Yang Xiaoguang.Analysis and simulation of traffic state on expressway during incident [J].Journal of Traffic and Transportation Engineering,2008,8(2): 116-121.

[2] 王元庆,周伟,吕连恩.道路阻抗函数理论与应用研究[J].公路交通科技,2004,21(9):82-83.

Wang Yuanqing,Zhou Wei,Lv Lianen.Theory and application study of the road traffic impedance function [J].Journal of Highway and Transportation Research and Development,2004,21(9): 82-83.

[3] 朱伟权.山东省公路信息管理系统设计和最短路径问题研究[D].长春:吉林大学,2006.

Zhu Weiquan.Design of the Highway Network Information Management System of Shandong Province and Study on the Shortest Path [D].Changchun: Jilin University,2006.

[4] 马永锋.公路网GIS数据组织方法及公路网多目标最优出行路径研究[D].天津:河北工业大学,2004.

Ma Yongfeng.Research on Data Organization Method in Highway Network GIS and the Optimization of Transit Route with Many Goals in Highway Network [D].Tianjin: Hebei University of Technology,2004.

[5] 郭忠印.道路安全工程[M].北京:人民交通出版社,2012.

Guo Zhongyin.Road Safety Engineering [M].Beijing,China Communications Press,2012.

[6] 陈富坚.灾变事件下高速公路网交通组织管理技术研究[D].上海:同济大学,2011.

Chen Fujian.Catastrophic Event Expressway Network Traffic Management Research [D].Shanghai: Tongji University,2011.

[7] 郭永基.可靠性工程原理[M].北京:清华大学出版社,Springer出版社,2002.

Guo Yongji.Reliability Engineering Principles [M].Beijing: Tsinghua University Press,Springer Press,2002.

[8] Dijkstra E W.A note on two problems in connection with graphs.[J].Numerische Mathematik,1959,1(1):269-271.

[9] 王峰,李德仁,杨树强,等.地理信息系统三十年 [J].计算机工程与科学,1995(2):83-92.

Wang Feng,Li Deren,Yang Shuqiang,et al.Geographic information systems: developments of three decades [J].Computer Engineering & Science,1995(2):83-92.

[10] Ben Chang,Mark Scardina,Stefan Kiritzov.Oracle9i XML Handbook [M].California: Oracle Press,2001.