土体剪胀性对地基承载力的影响

胡世敬，姚圣磊，余 苗

(1.贵州交通职业技术学院，贵州 贵阳 550008；2. 重庆交通大学 交通土建工程材料国家地方联合工程实验室，重庆 400074)

土体由于其颗粒骨料堆积而成的特点而具有两个基本特性：①压硬性，即土的强度和刚度随压应力增大而增大；②剪胀性，即土体的体积应变和剪应力有关[1]。笔者通过理论和有限元分析，讨论剪胀性对地基承载力的影响，以期为工程建设和设计提供一定的参考意义。

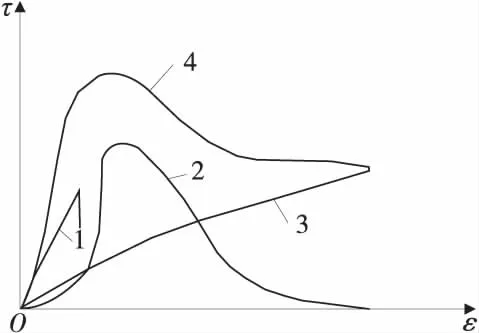
1—凝聚分量；2—剪胀分量；3—摩擦分量；4—实测强度

T. W. Lambe[2]将土的抗剪强度分为3个基本分量：凝聚分量、剪胀分量和摩擦分量，如图1。随着应变的增大，剪胀充分发挥作用，剪胀分量达到峰值；到达某一应变后，土体体积不再增加，剪胀分量也逐渐消失。

有关剪胀角的描述并不统一，剪胀角在滑移线场理论中主要有两种定义[3]：①实际塑性应变ε与剪切应变γ之间夹角；②破坏面(应力滑移线)与速度矢量方向的夹角[4]。笔者采用后者，如图2。

陈祖煜[5]分析了具有剪胀性的地基，岩土材料的剪胀角对地基承载力的影响。笔者基于文献[6-8]，采用ABAQUS有限元软件，根据GB 50007—2011《建筑地基基础设计规范》(以下简称《规范》)规定的地基极限承载力判定标准，给出了地基承载力的数值计算方法，分析了剪胀角对地基承载力的影响，确定地基承载力时应如何考虑土体材料剪胀性的影响，使得工程设计更加经济合理。

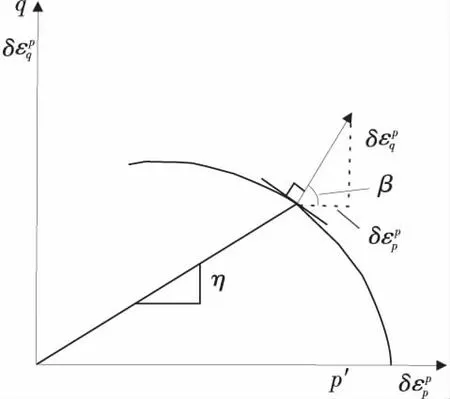
图2 应力比和剪胀角Fig.2 Stress ratio and dilatancy angle

1 Mohr-Coulomb对应的剪胀方程

经典弹塑性本构理论Mohr-Coulomb采用的流动法则为[9-10]：

(1)

对于Mohr-Coulomb相关联的流动法则，塑性势函数g与屈服函数f相同。

由式(1)可以得到：

(2)

(3)

从而可以得到剪胀方程[9]：

(4)

而Mohr-Coulomb理论对应的破坏准则(用p，q，θσ表示)为[11]：

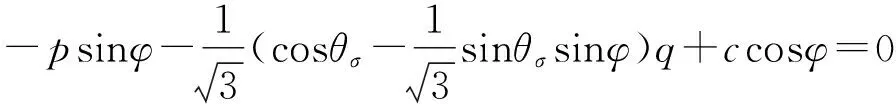
(5)

将式(4)代入式(5)，可以得到：

(6)

式中：φ为内摩擦角；ψ为剪胀角。

显然，式(6)中d<0，只能描述体积膨胀性(剪胀)的。

综上，Mohr-Coulomb破坏准则能考虑岩土材料的剪胀性，若要考虑土体材料的剪胀性，需要用Mohr-Coulomb进行计算。笔者在Mohr-Coulomb模型基础上，借助于有限元软件ABAQUS对条形地基承载力进行数值模拟分析。

2 地基承载力有限元分析

2.1 土体模型

土体材料的屈服准则采用Mohr-Coulomb等面积圆屈服准则，根据《规范》规定的条形地基承载力的确定方法进行数值模拟。

取条基宽度B=1 m，即地基承载力作用的部分，并将网格加密，材料的黏聚力c=70 kPa，内摩擦角φ=30°或20°，弹性模量E=200 MPa，泊松比υ=0.3。由于求解的是平面应变问题，且具有对称性，故取一半进行分析。几何图形和有限元网格如图3。

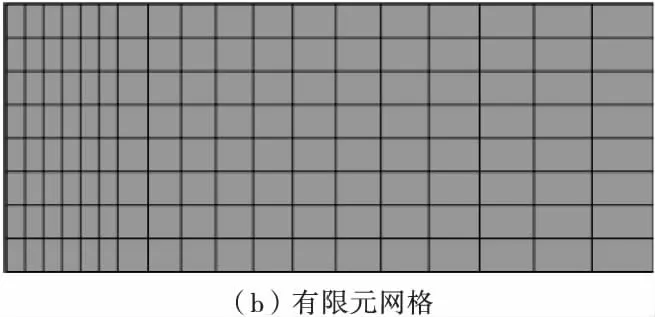
图3 几何模型及有限元网格Fig.3 Geometric model and finite element grid

荷载施加过程采用位移增量法，以研究地基土破坏的渐进过程。考虑土体重度和初始应力对承载力和变形的影响，将模型底部边界、左部边界约束其水平和垂直位移，对称边界约束其水平位移。

2.2 计算结果

图4为位移云图(ψ=φ=30° 时)，可见，其与常见的实际地基土破坏模式非常相近，说明有限元分析能真实反映地基土的破坏形态。

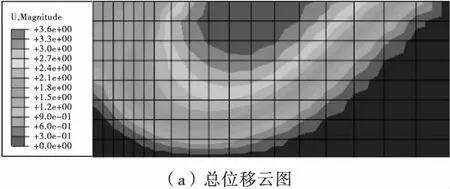
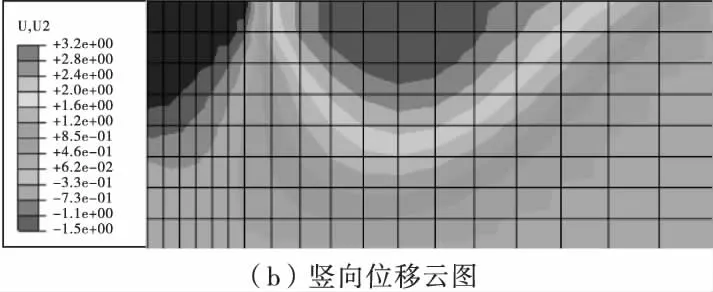
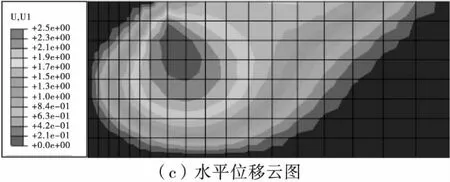
图4 有限元分析位移云图Fig.4 Cloud picture of displacement

图5是等效塑性应变云图(ψ=φ=30° 时)。分析可知，土体的塑性应变主要发生在地基下一定深度范围内，以及基础侧面一定宽度范围内。

图5 等效塑性应变云图Fig.5 Cloud picture of equivalent plastic strain

由图6可知，地基的极限承载力随剪胀角的增加而增大，曲线可分为3个阶段：

1)剪胀角在0～10°(φ=20°)，或0～15°(φ=30°)时为初始增加阶段，极限荷载有一定幅度的增加。

2)剪胀角在10～15°(φ=20°)，或15～25°(φ=30°)为继续增长阶段，极限承载力增幅较大。

3)剪胀角15～20°(φ=20°)，或25～30°(φ=30°)为趋稳阶段，尽管随着剪胀角的增加，但极限承载力增加不大，基本上趋于平稳。

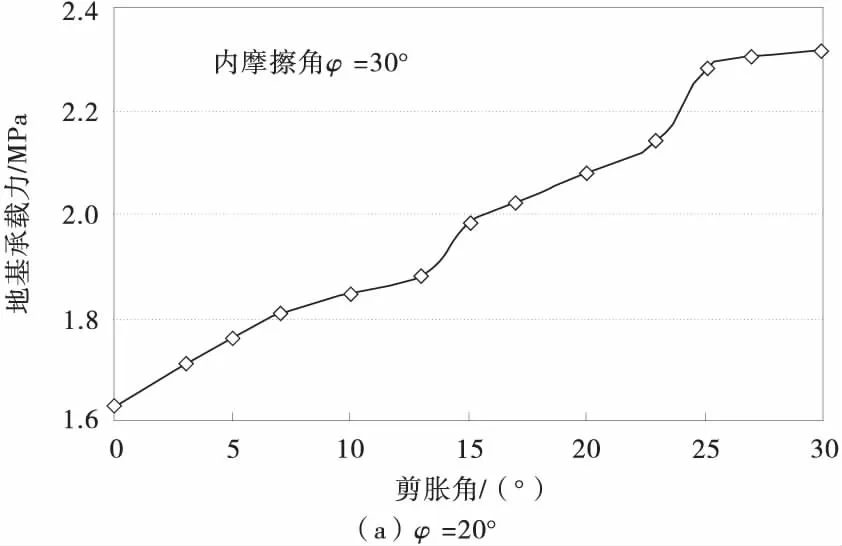
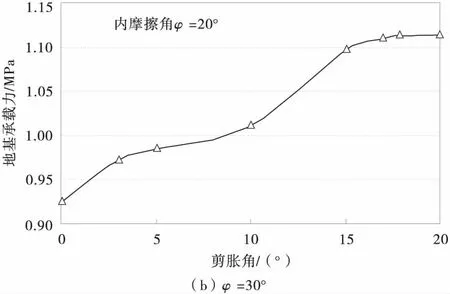
图6 不同内摩擦角对应的地基承载力与剪胀角变化关系Fig.6 Relation of bearing capacity of ground vs dilatancy angle ψ

对应于特定内摩擦角，当地基承载力随着剪胀角的增加而基本不变时，剪胀角即为合理剪胀角。因此由图6可知：当用有限元分析极限地基承载力时，剪胀角的合理取值范围：ψ=(3/4～5/6)φ。

当采用不同剪胀角计算对应于相应地基承载力的极限荷载时，由于剪胀角的影响，随着剪胀角的增加，导致极限地基承载力增加，并且位移矢量图大幅增加(图7)，这充分说明剪胀角对承载力的影响较大。

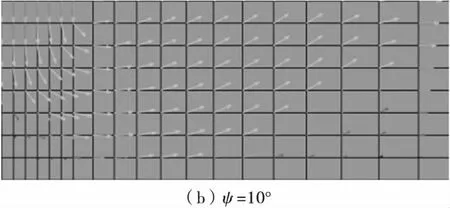
图7 不同剪胀角对应的位移矢量图Fig.7 The vector of displacement corresponding todifferent dilatancy angle

传统塑性力学理论在分析土体极限平衡时，假定剪胀角与内摩擦角相等。采用有限元分析极限地基承载力时，剪胀角小于内摩擦角，即ψ<φ，并且大量实验和工程实践表明[12-15]：有限元计算结果与岩土材料的基本特性较为相符。

3 结 论

研究得出以下结论：

1)摩尔-库伦模型及剑桥模型均能考虑土体的剪胀性和剪缩性。

2)根据ABAQUS有限元软件的摩尔-库伦模型，采用位移增量加载法模拟地基土的失稳破坏过程，并确定条形地基承载力极限荷载。

3)地基承载力随剪胀角的增加而增加，在计算地基承载力时必须考虑土体剪胀性的影响。

4)当采用有限元法计算地基极限承载力时，应考虑剪胀角的合理取值，即：ψ= (3/4～5/6)φ，以期得到较为可靠的计算结果。

[1] 沈珠江.理论土力学[M].北京:中国水利水电出版社,2000.

Shen Zhujiang.Theory of Soil Mechanics[M].Beijing:China Water Conservancy and Hydropower Press,2000.

[2] Lambe T W.A mechanistic picture of shear strength in clay [C]//Proc of ASCE Research Conference on Shear Strength of Cohesive Soils.Colorado,USA:University of Colorado Boulder ColoPress,1960.

[3] 邓楚键,郑颖人,王凯,等.有关岩土材料剪胀的讨论[J].岩土工程学报,2009,31(7):1110-1114.

Deng Chujian,Zheng Yingren,Wang Kai,et al.Some discussion on the dilatancy of geotechnical materials[J].Chinese Journal of Geotechnical Engineering,2009,31(7):1110-1114.

[4] David Muir-Wood.Soil Behavior and Critical State Soil Mechanics [M].New York:Cambridge University Press,1990.

[5] 陈祖煜.土力学经典问题的极限分析上、下限解[J].岩土工程学报,2002,24(1):1-11.

Chen Zuyu.Limit analysis for the classic problems of soil mechanics[J].Chinese Journal of Geotechnical Engineering,2002,24(1):1-11.

[6] 张国祥.潜在滑移线理论及浅基承载力分析[J].长沙铁道学院学报,1997,15(2):95-99.

Zhang Guoxiang.Potential sliding curve theory and analysis of ground bearing capacity[J].Journal of Changsha Railway University,1997,15(2):95-99.

[7] 张培文,陈祖煜.剪胀角对地基承载力的影响[J].岩土力学,2006,27 (3):463-465.

Zhang Peiwen,Chen Zuyu.Significance of soil dilatancy in bearing capacity of ground[J].Rock and Soil Mechanics,2006,27(3):463-465.

[8] 赵金勇,蒋刚,杨磊,等.剪胀角对地基极限承载力影响的有限元极限分析[J].南京工业大学学报,2008,30(5):28-32.

Zhao Jinyong,Jiang Gang,Yang Lei,et al.Effect of shear dilatancy angle on ultimate bearing capacity of foundation by FEM limit analysis[J].Journal of Nanjing University of Technology,2008,30(5):28-32.

[9] 陈愈炯,俞培基,魏汝龙.论土的剪胀性[J].水利学报,1964(6):76-80.

Chen Yujiong,Yu Peiji,Wei Rulong.Soil dilatancy theory[J].Hydraulic Engineering,1964(6):76-80.

[10] 孔位学,芮勇勤,董宝弟.岩土材料在非相关联流动法则下剪胀角选取探讨[J].岩土力学,2009,30(11):3278-3282.

Kong Weixue,Rui Yongqin,Dong Baodi.Determination of dilatancy angle for geomaterials under non-associated flow rule[J].Rock and Soil Mechanics,2009,30 (11):3278-3282.

[11] 郑颖人,沈珠江,龚晓南.岩土塑性力学原理[M].北京:中国建筑工业出版社,2002.

Zheng Yingren,Shen Zhujiang,Gong Xiaonan.The Principles of Geotechnical Plastic Mechanics[M].Beijing:China Architecture and Building Press,2002.

[12] 费康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010.

Fei Kang,Zhang Jianwei.The Application of ABAQUS in Geotechnical Engineering[M].Beijing:China Water Conservancy and Hydropower Press,2010.

[13] 庄茁,廖剑晖.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.

Zhuang Zhuo,Liao Jianhui.Based on ABAQUS Finite Element Analysis and Application[M].Beijing:Tsinghua University Press,2009.

[14] 夏志高.塑性力学[M].上海:同济大学出版社,1991.

Xia Zhigao.Plastic Mechanics[M].Shanghai:Tongji University Press,1991.

[15] 殷宗泽,邓肯J M.剪胀土与非剪胀土的应力应变关系[J].岩土工程学报,1984,6(4):24-40.

Yin Zongze,Duncan J M.A stress-strain relationship for dilative and non-dilative soils[J].Chinese Journal of Geotechnical Engineering,1984,6(4):24-40.