基于Sylvester结式低次拼接条件的研究

孙 原，李耀辉

（天津职业技术师范大学计算机科学系，天津 300222）

基于Sylvester结式低次拼接条件的研究

孙 原，李耀辉

（天津职业技术师范大学计算机科学系，天津 300222）

根据拼接中的主曲面和辅助曲面方程，利用同伦映射方法构造出含有单位区间变元的代数方程，应用Sylvester结式方法消去变元得到拼接曲面表达式。然后，假设该曲面表达式能够进行因式分解，分析G0和G1次光滑拼接中拼接曲面的次数最低时辅助曲面S（hi）应满足的条件。最后，运用Grobner基理论判断分解因式后各因式是否在主曲面和辅助曲面生成的理想中，从而得出符合条件的低次拼接曲面。

同伦映射；Sylvester结式；曲面拼接；分解因式；理想

0 引言

在计算机辅助几何设计（CAGD）的应用中，基于功能和美观要求常常需要将两个或两个以上的曲面进行光滑拼接，国内外很多学者对此研究出了不少方法[1]-[5]，[9]，[11]-[14]，希望得到次数尽可能低的拼接曲面，目前很多学者用Grobner基对自由曲面进行拼接研究，娄文平等[6]利用理想的Grobner基得到了求出所有代数拼接曲面的方法，并求出所有次数最低的GCk连续的拼接曲面。Tie-ru Wu[7]得到两个或以上的隐式代数曲面G1连续的拼接曲面的方法，并用Grobner基特性降低次数。现在拼接方法是相对成熟，工业需求中往往需要的是低次拼接曲面。给定主曲面S（fi）时，如何选取确定次数的辅助曲面S（hi）来使相应的拼接曲面次数最低似乎更让人们感兴趣。对于实际问题，很多人将最低次数拼接曲面归结为计算理想交[1]的Grobner基。但是，由于该方法计算复杂度高，难以实现，需另辟路径。吴文俊在文献[8]中提出特征列并对于两个垂直圆管在与轴垂直的平面截口处C1光滑拼接充要条件，但算法不能推广到高阶几何连续情形。李耀辉在文献[10]中讨论利用结式消元方法得出曲面拼接，实现简单且效率高。本文就是利用结式消元理论讨论两二次曲面作为主曲面且其轴垂直的平面截口处G0和G1光滑拼接时的所满足最低次拼接条件。

1 拼接曲面构造

设两代数曲面S（f1），S（f2）是需要拼接的主曲面，S（h1），S（h2）是两截面即辅助曲面，过渡曲面B从S（f1，h1）处开始过渡到S（f2，h2）并且光滑连接。由同伦概念可知，设X，Y是两个弧式连通的Hausdorff空间，如果存在一个映射H：X×I→Y，其中I是单位区间0≤t≤1，使得对于所有的x∈X有H（x，0）=f0（x），H（x，1）=f1（x），则说f0，f1在映射H：X×I→Y是同伦的。现将两被接拼曲面考虑为两个Hausdorff空间，其中的过渡曲面（即拼接曲面B）认为是两曲面对应点的弧式连通函数。连通函数的连续性保证了过渡曲面的连续性。这样，曲面的拼接问题转化为弧式连通函数的计算问题。根据同伦方法中连续变换的理论，f1在H的作用下映射为f2，辅助曲面h1映射为h2。这样，李耀辉[10]得出如下定理：

定理1 对于代数曲面f1，f2及其对应的过渡曲面h1，h2，构造如下方程组

并利用Sylvester结式消去变元t，得到方程B满足：

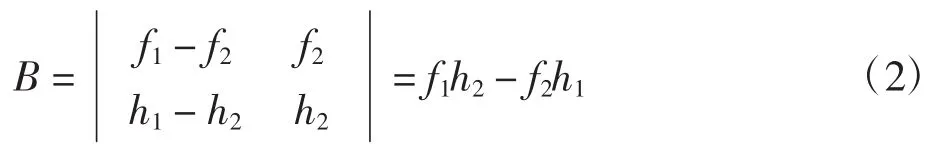
即B为Gk连续拼接曲面。

2 两圆柱拼接G0连续存在的最低次条件

若fi是二次主曲面，hi是一次辅助曲面，由以上定理可知拼接曲面满足G0（即k=0时）连续时，tdeg（fi。上述定理是针对曲面拼接的一般情况得到的，即三次拼接曲面总是存在的且当结式不能够进行因式分解时该结式就是拼接曲面。是否存在次数更低的拼接曲面。因为在工程实践中拼接曲面的次数越小，越容易实现。因此，我们研究在什么情况下，可以使拼接曲面B的次数尽可能的降低。

首先考虑的一种情况，主曲面是两圆柱面且两轴垂直时，在与轴垂直的平面截口处G0光滑拼接时满足的条件：给定两个轴垂直且半径分别为r1，r2的圆柱

两辅助曲面分别为：

其中：d1，d2分别为截距。由式（2）可以得到G0连续时的拼接曲面表达式为：

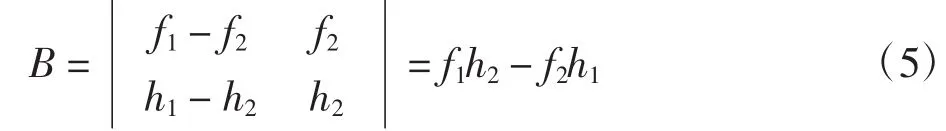
将（3），（4）式代入（5）式得到

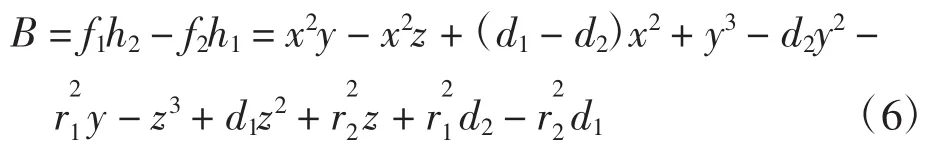
其中：m，n，a，a1，a2，a3，b1，b2，b3，c1，c2，c3，d0均为参数，将式（6）与式（7）的系数对比，可以得到20个关于系数的方程，分别求解系数方程，得到两个与r1，r2，d1，d2有关的等式即：和d1=d2，从而进一步推出r1=r2。

即可以得出结论，两圆柱面且两轴垂直时，G0连续时要得到最低拼接曲面，则必须满足如下条件：d1= d2，且r1=r2。

3 两圆柱拼接G1连续时存在的最低次条件

同样还是两圆柱曲面，设表达式与（3），（4）一样，若要满足G1（即k=1）次光滑连续，则根据式（2），此时的拼接曲面应为：

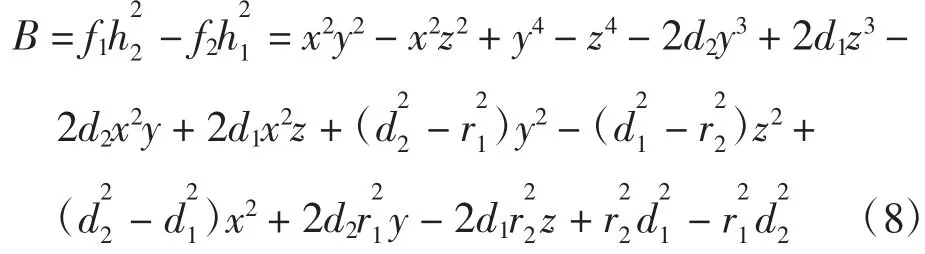
由上式可知tdeg（B）≤4，故此处可假设B是可以分解因式的，先假设B可被分解成一个一次多项式与一个三次多项式相乘，即：

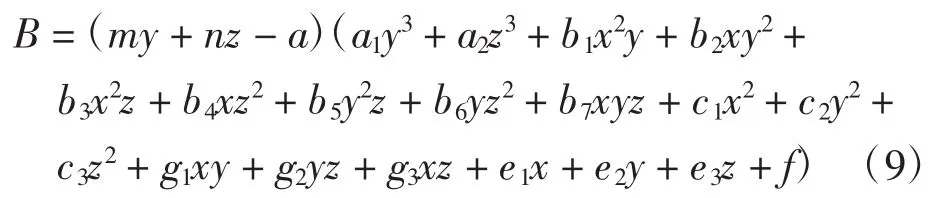
将式（9）因式分解，分别与式（8）的系数做比较，可得出如下关系：

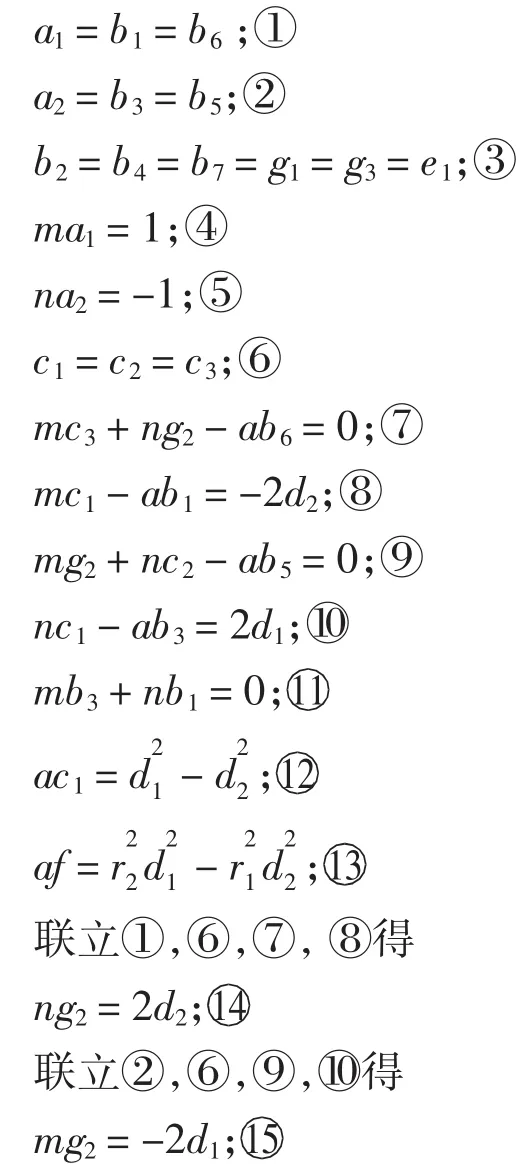
讨论情形1，当d1≠0时，由④，⑤，⑭，⑮可分别将1，a2分别用m表示出来，再代入⑪式中，得

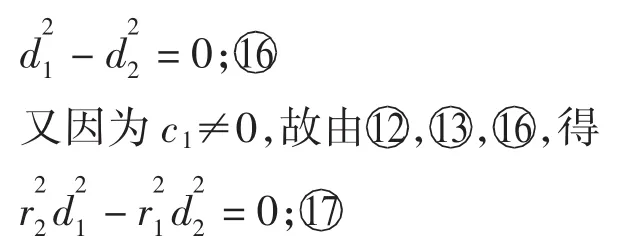
综合上述可知，d1≠0时，由⑯和⑰可知，存在三次拼接曲面，当且仅当：

情形2，当d1=0时，则d2=0，且r1=r2，求出相关的系数，将得到的各式子代入原式（9）的展开式中得到：

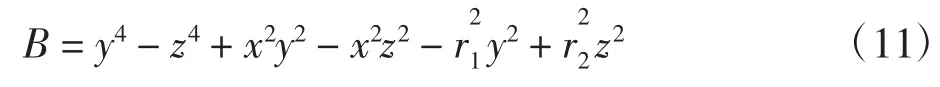
由上式可看出当r1=r2=r时可分解为

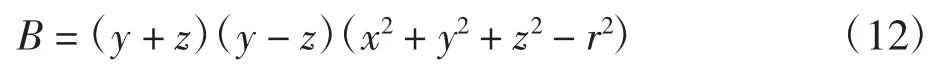
定理2[10]如果所得结式B可以分解为若干个因式的乘积，则其中必有一项B′是f1，f2分别沿曲线B（f1，h1），B（f2，h2）Gk连续的拼接曲面。

故根据上述定理可以判断式（12）中的x2+y2+z2-r2即为拼接曲面，从而达到了降次的效果。由上式推导得出的结论我们可以推广到一般情形，得出如下定理：

推论1：当二次曲面（椭圆面，抛物面，双曲面，各曲面的系数相等）轴线垂直时，在各项系数都相等情况下，与轴垂直的平面截口处G1光滑拼接能得到的三次拼接曲面条件为：

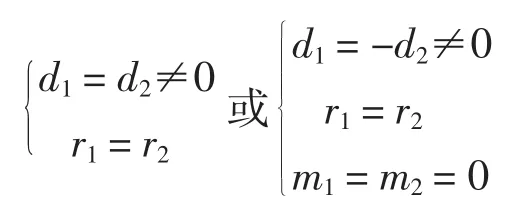
存在二次拼接曲面条件为：

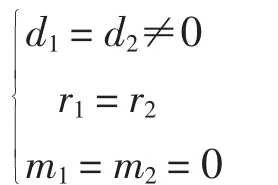
其中：d1，d2为截面的截距，m1，m2分别为y，z前的系数，r1，r2分别为二次曲面的常数。

证明：设二次曲面可表示为：

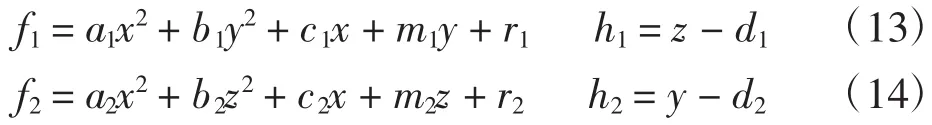
将式（13），（14）代入式（2）中，得

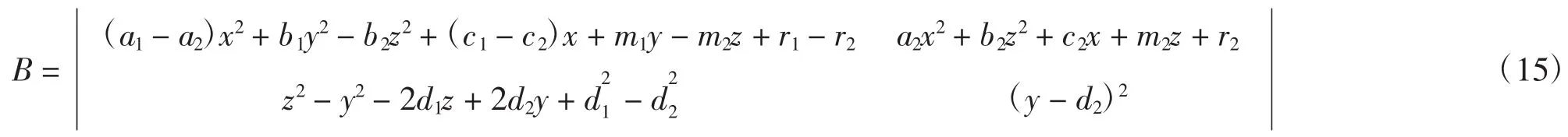
因为第二行只含y，z要想上式可分解，则只能考虑是关于y，z的因子，故此处必有a1=a2=a，c1=c2= c，r1=r2=r，又因为第二行的z2，y2的系数为±1，则此时要想可分解，则必有d1=d2，且第一行中b1=b2，m1=m2，故可提出公因式（z-y），可把式子表示成如下形式：

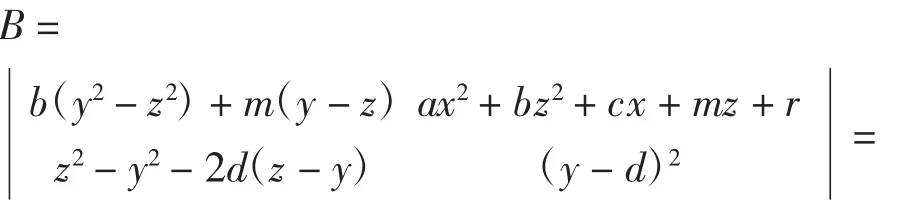
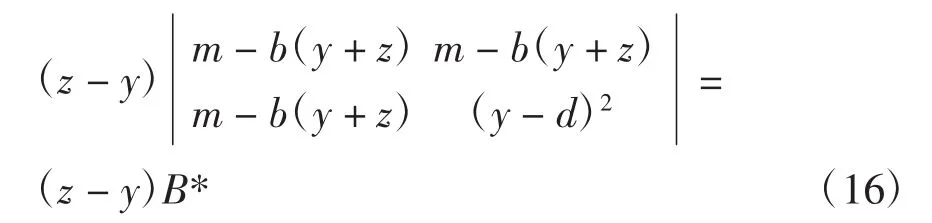
由式（16）可以看出，提出公因式后第一列的式子均只剩下一次项，而第二列是二次多项式，交叉相乘后tdeg（B*）=3，由定理2可知tdeg（B）=tdeg（B*）= 3，得到最低次拼接曲面为三次。同样，在d1=-d2时，存在m=0的情况下得到公因式（x+y），并得到最低次为三次拼接曲面。

那么要得到最低次拼接曲面为二次时，同样可用上述方法分析得出，当m=0，d=0，时，得到

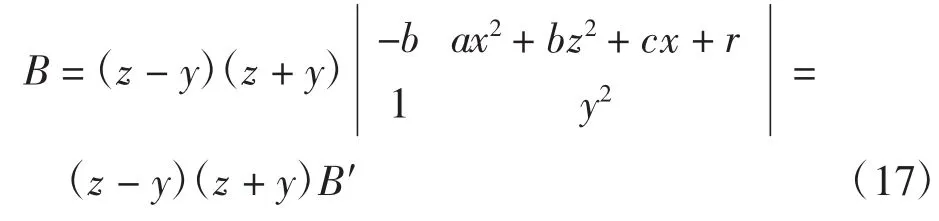
可以得出tdeg（B′）=tdeg（B）=2

4 实例

例1：两不相交圆柱G0光滑拼接

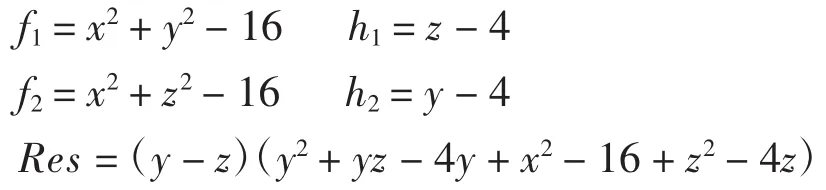
拼接曲面为：

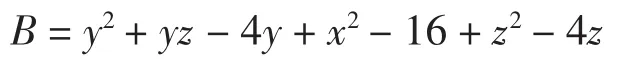
两圆柱G0光滑拼接时存在的二次拼接条件满足所讨论的即：d1=d2且r1=r2，得到的拼接图形如图1所示，图（a）为式Res（没有去除多余因子时）效果图，（b）图是式B（即去除多余因式后）的拼接效果图，从图中可以看出去除多余因子后不仅不会影响图形拼接效果，而且还能达到降低次数的效果。

图1 两不相交圆柱G0光滑拼接

例2：两相交圆柱G1光滑拼接

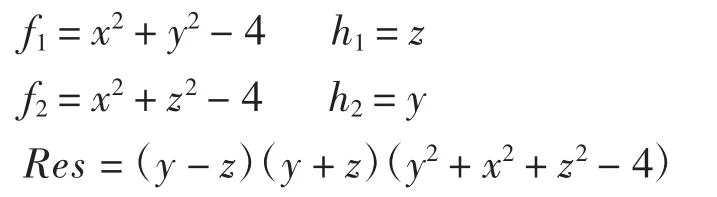
拼接曲面为：

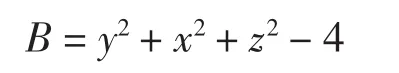
满足上述讨论的情形2，即当d1=d2=0且r1=r2，可以得到最低次曲面拼接方程，拼接效果如下图2所示，（a）图为未除去多余因子时的效果图，因为两圆柱面相交，存在重合部分，不好看，为了美化图形，取值时分别取圆柱的一半从而消去中间重合的部分，形成所示的水管的洼槽形式如图2（b）图所示。

例3：两抛物面G1光滑拼接

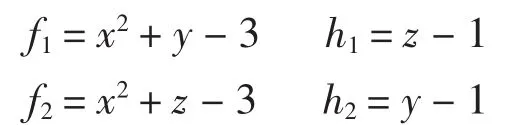
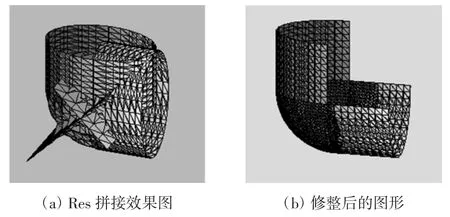
图2 两相交圆柱G1光滑拼接

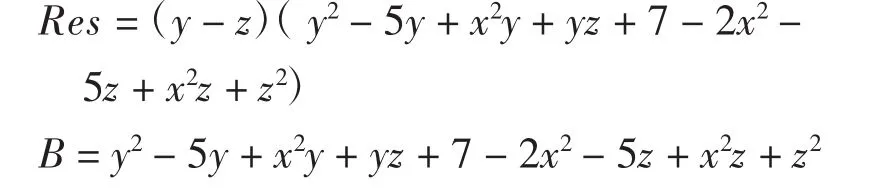
两抛物面拼接G1光滑拼接时，满足推论1，即tdeg（Res）=4时，d1=d2且r1=r2存在三次拼接曲面如图3所示：

图3 两抛物线G1光滑拼接

例4：两双曲面G1光滑拼接

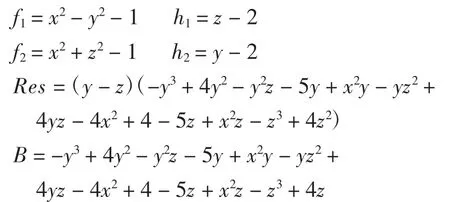
同样两双曲面拼接时，也满足推论1，此处只取双曲面的半页进行拼接得到的拼接图如图4所示：

图4 两双曲面G1光滑拼接

5 总结

本文讨论了基于结式曲面拼接情况下，寻找两垂直圆柱在与轴垂直的平面截口处Gk光滑拼接时得到最低次拼接面的条件，可以看出，若要满足G0次光滑拼接时的最低曲面只能是二次曲面，即在两圆柱的半径和辅助曲面的截距均相等时存在最低次为二次的拼接曲面；若要满足G1次光滑拼接时，存在最低次为二次的拼接曲面当且仅当两截距均为零且两圆柱的半径相等时；存在最低次为三次拼接曲面时的条件为两圆柱的半径相等，且辅助曲面的截距的平方相等。并通过了大量的实验证明了该方法的正确性。并且将其推广到一般情况下的两个二次曲面拼接，得到G1光滑拼接曲面满足的低次拼接（二次或三次多项式）推论形式。并证明其正确性，目前仅考虑了被拼接图形是同类型的图形且截面垂直情况下，对于其它一般不同二次形的曲面拼接以及截面不垂直情况下寻找最低次将是以后要研究的重点。

［1］ Joe Warren.Blending algebraic surfaces[J].ACM Transactions on Graphics，263-278.1989.

［2］ Thomas w.Sederberg.Technique for cubic algebraic surfaces part two[J].Computer Graphics and Application，1990，10（5）：12-21.

［3］ Erich Hartmann.Blending an implicit with a parametric surface[J].Computer Aided Geometric Design，1995，Vol.12（5）：825-835.

［4］ Erich Hartmann，Parametric Gn blending of curves and surfaces[J].The Visual Computer，2001，Vol.17（1）：1-13.

［5］ 程进三，高小山.构造两个曲面的拼接曲面[J].工程图学学报，No.1，2005：39-44.

［6］ 娄文平，冯玉瑜，陈发来，等.构造代数Blending曲面的Grobner基方法[J].计算机学报，2002，Vol.25（6）：599-605.

［7］ Tie-ru Wu.On blending of several quadratic algebraic surfaces[J].Computer Aided Geometric Design，2000，Vol.17（8）：759-766.

［8］ 吴文俊，王定康.CAGD中代数曲面拟合问题[J].数学的实践与认识，1994，6（3）：26-31.

［9］ Wu Tieru，Lei Na，Cheng Jinsan.Wu Wen-tsun Formulae for the Blending of Pipe Surfaces[J].Northeast Math，2001，17（4）：383-386.

［10］李耀辉.基于结式方法的代数曲面拼接[J].计算机工程与应用，2008，44（29）：17-21.

［11］王贝，李基拓，陆国栋.空间趋向曲线引导的网格曲面拼接[J].浙江大学学报（工学版），2013，47（11）：203-209.

［12］李云东.二次与三次隐式代数曲面沿平面截口光滑拼接[D].四川：西南交通大学，2006.

［13］李耀辉，宣兆成，武志峰.二次代数曲面拼接中的光顺处理[J].计算机应用，2014，34（7）：2054-2057.

［14］郭明浩.含参代数曲面族的光滑拼接及有理参数化[D].吉林：吉林大学，2012.

Computing the Lowest Degree Condition for Blending Surface by Using Sylvester Resultant

SUN Yuan，LI Yao-hui
（Department of Computer Science，Tianjin University of Education and Technology，Tianjin 300222）

Constructing blending equations on algebraic surfaces and their auxillary surface by using the homotopy mapping method which containing the unit interval variables first.Then eliminate the variable with the Sylvester resultant method，so we can get the blending surface expression.According to the Sylvester elimination method of reverse assuming the expressions can be factorization，analysis and discussion auxiliary surface S（hi）should satisfy the conditions of the minimum number of surfaces when G0and G1smooth connection.Then judge the factored polynomial by Grobner base whether or not in the ideal.So we can get the low degree blending surface meets the conditions.

Homotopy；Sylvester resultant；Surface blending；Factorization；Ideal

TP391.7

A

2095－0926（2014）04－0001－04

2014-00-00

孙 原（1989—），女，硕士，主要研究领域为符号计算,结式理论及应用；李耀辉（1964—），男，教授，博士，主要研究符号计算，计算机辅助几何设计，结式理论及应用.