球形弹丸正撞击碎片云头部形状的辨识*

安 凯

(山东航天电子技术研究所,山东 烟台 264003)

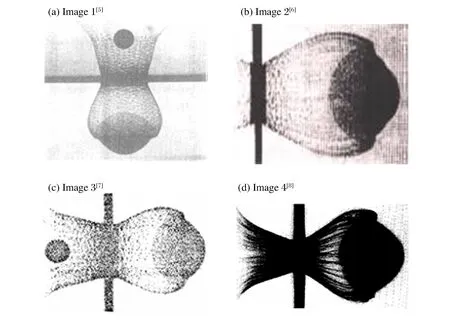
图1 超高速撞击实验碎片云图Fig.1 Debris clouds from hypervelocity impact experiments

航天器外壳受到空间碎片的超高速撞击产生的高速碎片云，可能对航天器内部的仪器设备造成灾难性的破坏，甚至导致航天器过早失效。研究碎片云的形状与运动特性，对于定量预测航天器内部仪器设备的损伤程度，并进行相应的防护设计，具有十分重要的意义。因此，这个问题受到高度重视，各种不同的碎片云模型被提出或改进。以球形弹丸正撞击靶板为例，H.F.Swift[1]给出的碎片云运动模型为一个膨胀的球壳，碎片云质量均匀地分布在球壳上。碎片云的运动可分解为质心沿弹道方向的直线运动和以质心为中心的膨胀。W.P.Schonberg等[2]给出的碎片云模型与Swift模型类似，不同的是内部为弹丸碎片云，外部是一个缓冲板碎片云形成的球壳。然而许多实验结果表明，碎片云的外形显然不是一个球[3-4]，而是更象一个旋转椭球面，因此又为碎片云建立了旋转椭球模型。F.K.Schäfer[4]提出了一个球形弹丸正撞击金属薄板的碎片云模型，在忽略反溅碎片云的前提下，碎片云模型分为3部分：(1) 缓冲板材料碎片云，其质量均匀分布在旋转椭球壳上；(2)弹丸材料碎片云，分布在一个球壳上，且头部内切于缓冲板材料形成的旋转椭球壳碎片云；(3)弹丸材料中心大碎片，位于弹丸材料球壳碎片云头部。然而，无论是球形碎片云模型，还是旋转椭球壳碎片云模型，都没有通过对实验图像进行边缘提取、并与相关模型进行拟合、以证实模型的正确性。

从许多超高速撞击实验获得的碎片云图片可以看出，碎片云形状与旋转椭球存在明显差异。图1是4幅超高速撞击实验的碎片云图片[5-8]，由此可以看出球形弹丸正撞击金属薄板产生碎片云的大致形状：尾部为旋转曲面壳体，头部为前面呈草帽状的高密度区域[9]。草帽形状的确定主要是“草帽顶”形状的确定。

本文中，将通过图像处理方法提取碎片云“草帽顶”的边缘图像，并以二次曲线的旋转曲面与此拟合，以选择最优的拟合曲面。

1 碎片云形状的拟合

由实验可以得到碎片云的三维图像，但从文献中获取的往往是在平面上的投影。但对于正撞击的情形，碎片云外形可以视为旋转曲面，其形状由它在平面上的正投影图像(如不混淆，以下简称碎片云图像)的形状唯一确定。对于碎片云图像，通过图像处理方法，例如图像锐化[10]，可以提取出边缘曲线。假定(xi,yi)是碎片云的边缘曲线，i=1,2,…,n，n为数据点个数。如果碎片云图像的对称轴平行于坐标轴，与此拟合的二次函数的一般形式为：

y2+Ay+Bx2+Cx+D=0

(1)

y+Bx2+Cx+D=0

(2)

式中：A、B、C、D为待定拟合系数。式(1)当B<0时为双曲线，当B>0时为椭圆；式(2)为抛物线。

由于图像本身以及获取过程的各种因素，图像不可能严格遵循某一二次函数，所谓其形状为某一二次函数，只能是更加接近而已。于是就产生了“接近”程度的度量问题。

对于抛物线，一种常用的度量指标为：

(3)

式中：f(x)=-Bx2-Cx-D。

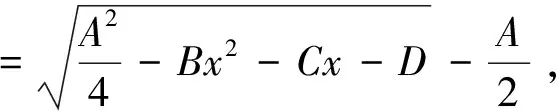
2 碎片云图像函数拟合方法

对于经图像处理获取的碎片云的边缘曲线(xi,yi)的函数拟合，是为了寻找拟合系数A、B、C、D,使度量指标M达到最小值。

2.1 抛物线拟合

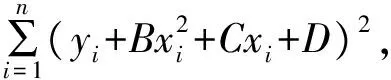
2.2 双曲线/椭圆拟合

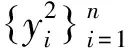
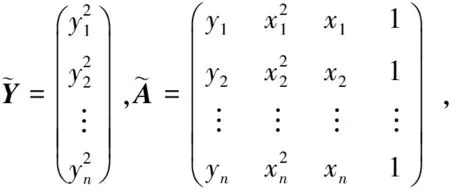
3 碎片云图像辨识

通过边缘提取可以得到碎片云的边缘曲线；通过二次函数拟合可以得到两种拟合曲线及其与边缘曲线拟合程度的度量指标；通过对度量指标的选择可以对碎片云图像进行辨识；通过对图1中不同来源碎片云图像的辨识，可以对碎片云形状给出结论。

3.1 图像1

利用上述方法进行抛物线拟合，拟合系数B、C、D分别为0.007 5、-5.066 7和883.394 7, 度量指标为37.870 5。

进行双曲线/椭圆拟合，拟合系数初值A、B、C、D分别为260、-1.168、784.638 7和-1.392 7，度量指标为129.014 2。利用变半径随机搜索算法进行搜索，但度量指标始终不小于37.870 5，因此辨识结果为抛物线。最优拟合结果如图2所示。

3.2 图像2

进行抛物线拟合，拟合系数B、C、D分别为0.004 3、-2.521 0和536.066 2, 度量指标为664.115 1。

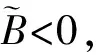
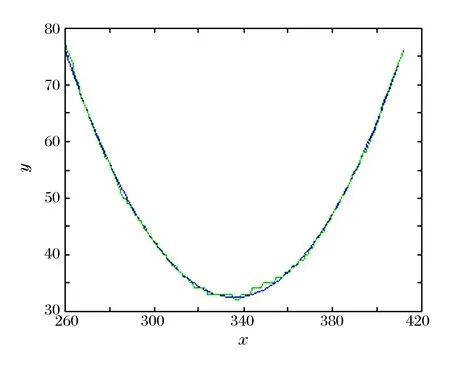
图2 图像1的抛物线拟合结果Fig.2 Parabola fitting result of image 1

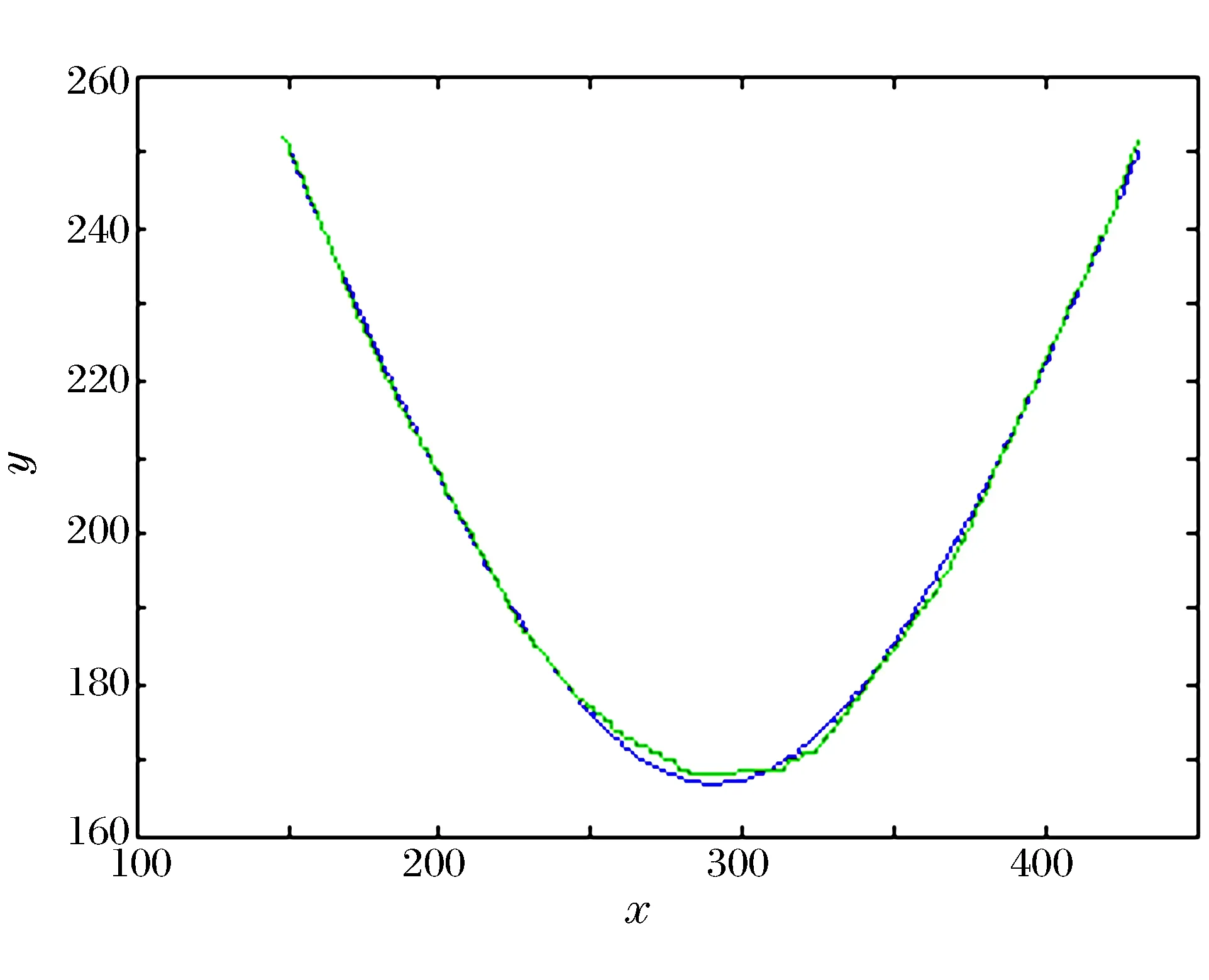
图3 图像2的椭圆拟合结果Fig.3 Ellipse fitting result of image 2

3.3 图像3

进行抛物线拟合，拟合系数B、C、D分别为0.015 7、-8.635 1和1 367.6, 度量指标为15.417 5。

进行双曲线/椭圆拟合，拟合系数初值A、B、C、D分别为405.649 2、-0.386 3、 212.817 1和-69 948，度量指标为945.921 4。利用变半径随机搜索算法进行搜索，但度量指标始终不小于15.417 5，因此辨识结果为抛物线。最优拟合结果如图4所示。

3.4 图像4

进行抛物线拟合，拟合系数B、C、D分别为0.012 5、-7.243 1和1 260.8, 度量指标为43.656 8。

进行双曲线/椭圆拟合，拟合系数初值A、B、C、D分别为399.634 7、0.749 2、 -435.313 3和23 180.429 1，度量指标为438 700，因此辨识结果为抛物线。最优拟合结果如图5所示。

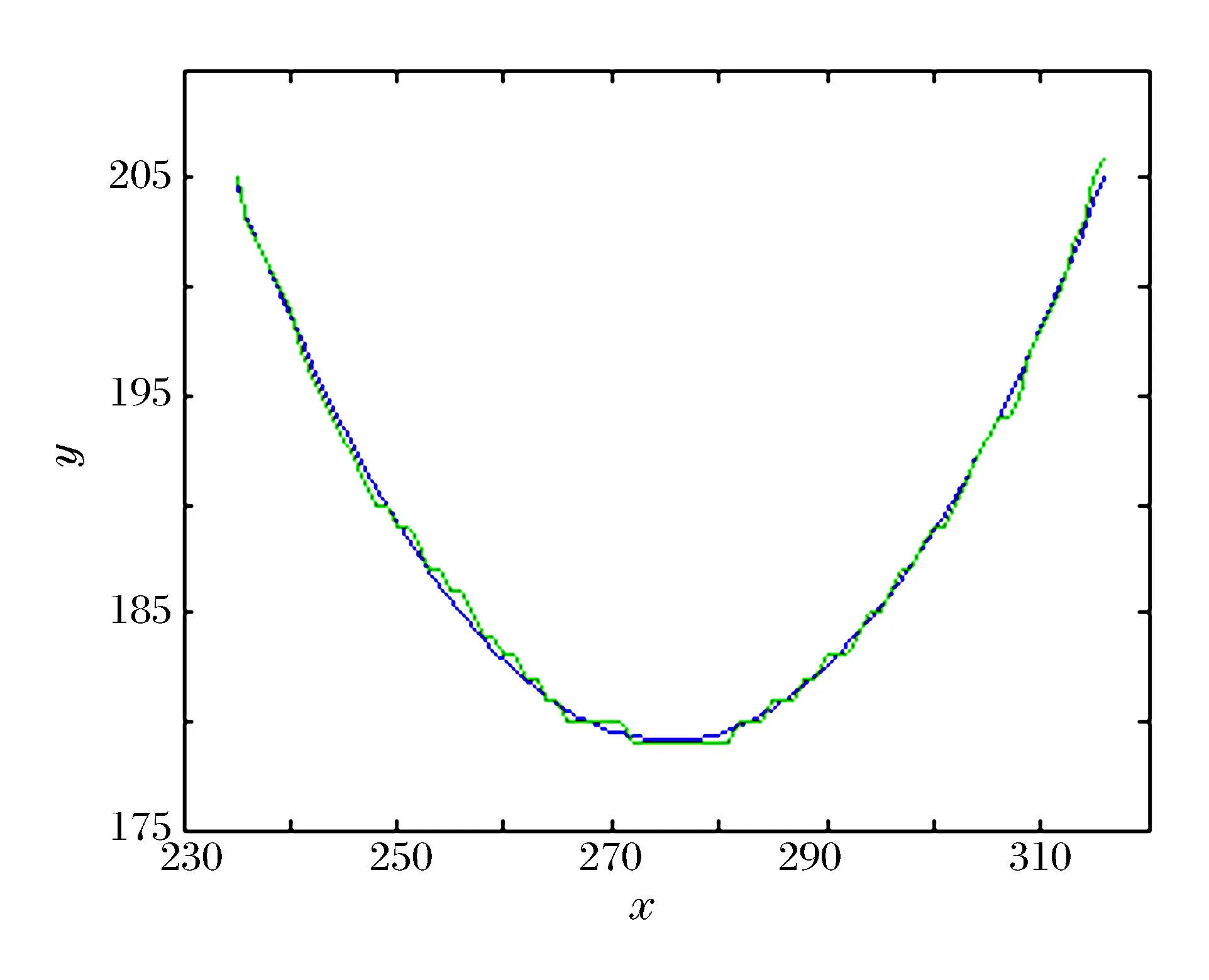
图4 图像3的抛物线拟合结果Fig.4 Parabola fitting result of image 3

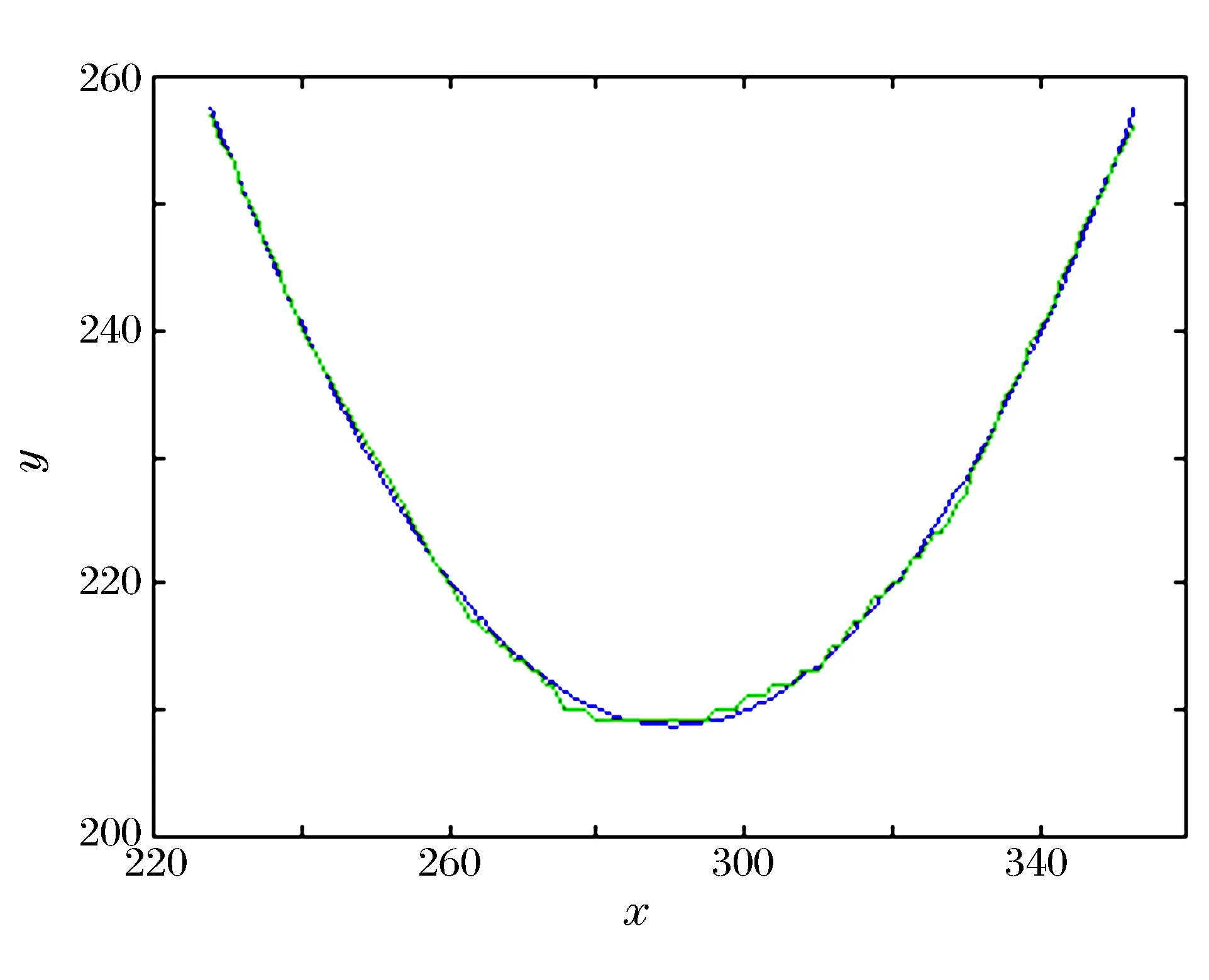
图5 图像4的抛物线拟合结果Fig.5 Parabola fitting result of image 4

4 结 论

上述辨识结果显示，4幅碎片云图像中有3幅头部形状更接近抛物线，有1幅更接近椭球，未发现接近双曲线的。尽管图像边缘提取过程中存在干扰，但从频率上看，似乎认为头部形状为抛物线、即碎片云前沿的形状为旋转抛物面更合理。

按照流体力学理论[12-13]，中空圆柱形管道中的稳定流，流体前沿速度的分布正是旋转抛物面。从弹孔中喷射出的碎片云不是稳定流，但上述辨识结果表明，其前沿的形状是旋转抛物面。这是巧合还是存在某种必然联系，需要进一步研究。

[1] Swift H F. Impact dynamics[M]. New York: John Wiley & Sons, 1982.

[2] Schonberg W P, Williamsen J E. Empirical hole size and crack length models for dual-wall systems under hypervelocity projectile impact[J]. International Journal of Impact Engineering, 1997,20(6):711-722.

[3] 唐蜜,柏劲松,李平,等.超高速撞击中影响碎片云形状因素分析[J].高压物理学报,2007,21(4):425-431.

Tang Mi, Bai Jing-song, Li Ping, et al. Factors analysis of debris cloud’s shape of hypervelocity impact[J]. Chinese Journal of High Pressure Physics,2007,21(4):425-431.

[4] Schäfer F K. An engineering fragmentation model for the impact of spherical projectiles on thin metallic plates[J]. International Journal of Impact Engineering, 2006,33(1):745-762.

[5] 贾光辉,黄海.超高速撞击航天器二次碎片云能量特性分析[J].北京航空航天大学学报,2007,33(3):257-260.

Jia Guang-hui, Huang Hai. Characters on kinetics energy of debris cloud in spacecraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007,33(3):257-260.

[6] 张伟,庞宝君,贾斌,等.弹丸超高速撞击防护屏碎片云数值模拟[J].高压物理学报,2004,18(1):47-52.

Zhang Wei, Pang Bao-jun, Jia Bin, et al. Numerical simulation of debris cloud produced by hypervelocity impact of projectile on bumper[J]. Chinese Journal of High Pressure Physics, 2004,18(1):47-52.

[7] 胡震东,黄海,贾光辉.超高速撞击碎片云特性分析[J].弹箭与制导学报,2006,26(1):747-749.

Hu Zhen-dong, Huang Hai, Jia Guang-hui. The characteristics of debris cloud produced by hypervelocity impact[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006,26(1):747-749.

[8] Poormon K L, Piekutowski A J. Comparisons of cadmium and aluminum debris clouds[J]. International Journal of Impact Engineering, 1995,17(4):639-648.

[9] Piekutowski A J. Formation and description of debris clouds produced by hypervelocity impact[Z]. NASA, 1996.

[10] Castleman K R. Digital image processing[M]. New Jersey: Prentice-Hall International, Inc, 1996.

[11] 安凯,邢进生,邱祖廉.模糊神经网络的二阶段变半径随机搜索算法[J].自动化学报,2000,26(5):616-622.

An Kai, Xing Jin-sheng, Qin Zu-lian. Two-stage random search algorithm of fuzzy neural network with variable radius[J]. Acta Automatica Sinica, 2000,26(5):616-622.

[12] Kundu P K. Fluid mechanics[M]. California: Elsevier Academic Press, 2004:283-285.

[13] Nakayama Y. Introduction to fluid mechanics[M]. Tokyo: Yokendo Co Ltd, 2000:82-94.