异型头部弹体增强侵彻性能机理研究*

刘坚成,黄风雷,皮爱国,柴传国,武海军

(北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

动能侵彻武器是打击加固和地下深埋目标的有效手段，提高动能侵彻武器的侵彻性能是当前该领域研究的热点。增强钻地弹侵彻能力的技术途径，主要包括提高着速、增加侵彻体截面动能和改进侵彻体头部结构。在一定的战术技术条件下，即给定着速、侵彻体总质量及弹径等参数后，影响侵彻性能的主要因素在其头部形状。

弹体头部对侵彻能力影响的研究由来已久，在机理研究方面，M.J.Forrestal等[1-2]基于空腔膨胀理论建立并验证了卵形头部弹体的侵彻阻力经验公式。S.E.Jones等[3]对具有y=f(x)一般形式的弹体头部进行受力分析，得到一个与它有关的量纲一常量——头部形状系数N*，并分析了N*与惯性阻力的关系。X.W.Chen等[4]从几何角度分析了多种不同弹体头部形状的头部系数N*。J.Zhao等[5]分析了侵彻过程中N*与速度的关系。R.C.Batra等[6]讨论了摩擦力在侵彻过程中的影响。

在常规弹速情况下，弹头形状对侵彻能力的影响尚不突出；但对高速或超高速侵彻，与头部形状相关的惯性阻力项增大，弹头形状成为影响战斗部侵彻性能的重要因素。本文中，基于高速或超高速侵彻，在经典的空腔膨胀理论基础上，基于双卵形异型头部设计，分析头部形状系数N*与双卵形特征参数的依赖关系，讨论不同异型头部弹体对其侵彻性能的影响规律，提出一种双卵形异型头部结构优化设计方案。

1 异型弹体设计与计算

1.1 基于空腔膨胀理论的侵彻体减阻异型头部设计

空腔膨胀理论起初是在对金属类延性材料的研究中建立与发展的[7]。R.C.Bishop等[8]首次推导了金属材料球形与柱形空腔膨胀的(准)静态表达式，R.Hill[9]在此基础上提出了金属材料球形空腔动态膨胀的表达式，M.J.Forrestal等[10]进行了深入研究，得到以下简单形式：

σr=AY+Bρ0V2

(1)

式中：Y和ρ0是靶板材料的无侧限抗压强度和初始密度。系数A、B为靶板材料系数，可通过拟合得到。该阻力项与对指数硬化金属材料的侵彻阻力项形式相同，由与靶板材料强度相关的静态阻力项和与侵彻速度相关的惯性阻力项组成。基于上述阻力模型，皮爱国[7]讨论了侵彻2024-O靶板和不同强度混凝土的静态阻力项及惯性阻力项在侵彻过程中所占比例。计算结果表明，靶板强度越高，静态阻力项在整个阻力函数中的比例越大；随着侵彻速度增加，惯性阻力项在整个阻力函数中的比例加大。

S.E.Jones等[3]对具有y=f(x)一般函数形式的头部形状弹体进行了受力分析，并给出了阻力的表达形式：

(2)

式中：p为弹体表面法向压力，f为弹靶摩擦力，F为在横坐标为x上的弹体运动方向合阻力。

结合J.D.Walker等[11]的研究工作，采用侵彻空腔表面的径向速度呈余弦分布，讨论弹体的侵彻压力。空腔表面径向速度为：

V=vcosθ

(3)

式中：v为弹体侵彻速度。结合空腔膨胀理论给出的空腔表面的径向应力和空腔膨胀速度关系，弹体表面径向应力和侵彻速度关系的近似表达式为：

p=σn=AY+Bρ0vcosθ2

(4)

结合S.E.Jones等[3]的工作，引入弹头形状系数：

(5)

则式(2)可写成：

F=πa2BN*ρ0v2+AY

(6)

由式(5)可知，N*为量纲一量且只与弹体头部几何形状相关，它定量地表征了弹体的头部形状，此系数可以作为评价弹体在侵彻过程中所受惯性阻力大小的物理量。由式(6)即侵彻体阻力表达式，当给定侵彻体直径、着速等条件时，侵彻体阻力的优化只与弹体头部系数N*有关。在工程实际中，出于侵彻稳定性及总体限制等考虑，穿甲弹/半穿甲弹等侵彻体的头部一般设计为卵形，且卵形头部母线曲径比φ一般为3～5，以避免过长的弹体头部[12]。本文中重点考察在φ=5的弹体头部长度范围内，采用双卵形侵彻体头部，以获得头部系数N*小于单卵形的优化设计方案。

为进一步比较在该类弹头形状的弹体中N*的变化情况，选取φ=3的弹体，结合N*的一般表达式(5)，可得该弹体头部系数N*的变化趋势及N*的变化率k，k=dN*/dx,如图1所示。

由N*-x曲线，对卵形头部，N*为单调增长的函数，且在前半部分增加较快，后半部分增长较慢。由k-x曲线，N*的变化在x/l=0.208处达到最大值。选定x/l=0.208两侧的一段区域进行改造，该段区域长度一般应控制在弹头长度的1/3以内，本文中以k>0.027 cm-1的区间为例进行优化设计，尽量减少此部分N*的增加量。改进的弹体头部形状示意图如图2所示，在弹体头部形状中引入锥形部分和卵形部分。图中,AEFHGDC为改进后的弹体围成的区域，由3个小区域组成。最外侧弧线ABG表示φ=5的弹体头部形状，弧线ODG表示φ=3的弹体头部形状。

(7)

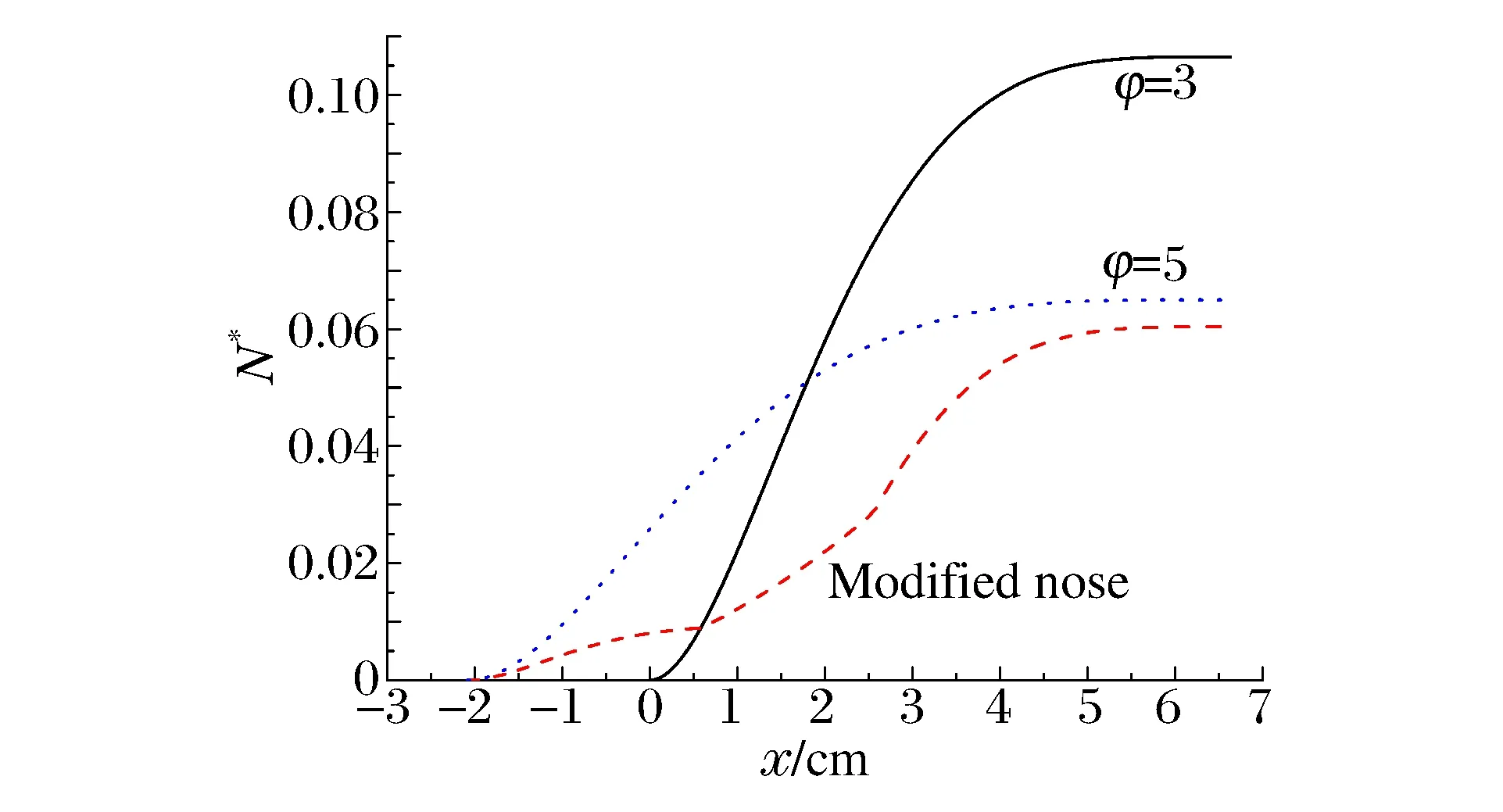
图3 φ=3、异型弹体和φ=5弹体的头部形状系数Fig.3 Relation between N* and nose position of φ=3, modified and φ=5 projectiles

该异型弹体表征的意义为，在介于φ=3和φ=5的头部形状中寻找一种相对优异的几何形状，以减小弹体在侵彻过程中所受的阻力。图3给出了φ=3、φ=5和改进后双卵形异型弹体的形状系数N*随位置的变化。在相同头部长度条件下，优化的双卵形异型头部形状系数N*低于单卵形头部。

1.2 异型弹体侵彻阻力计算分析

对双卵形异型头部弹体，如图4所示，侵彻阻力分为3个部分：尖端区域1为卵形，半径S1；中间部分区域2为锥形，两端距中轴线距离分别为a1和a2；根部区域3为卵形，半径S2。

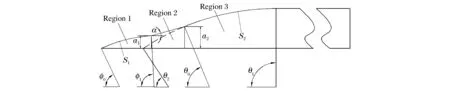
图4 异型头部弹体尺寸Fig.4 Dimension figure of modified nose

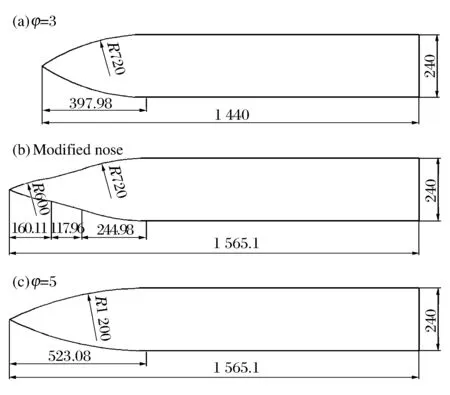
图5 φ=3、异型头部和φ=5的弹体示意图Fig.5 Dimension figure of φ=3, modified nose and φ=5 projectiles

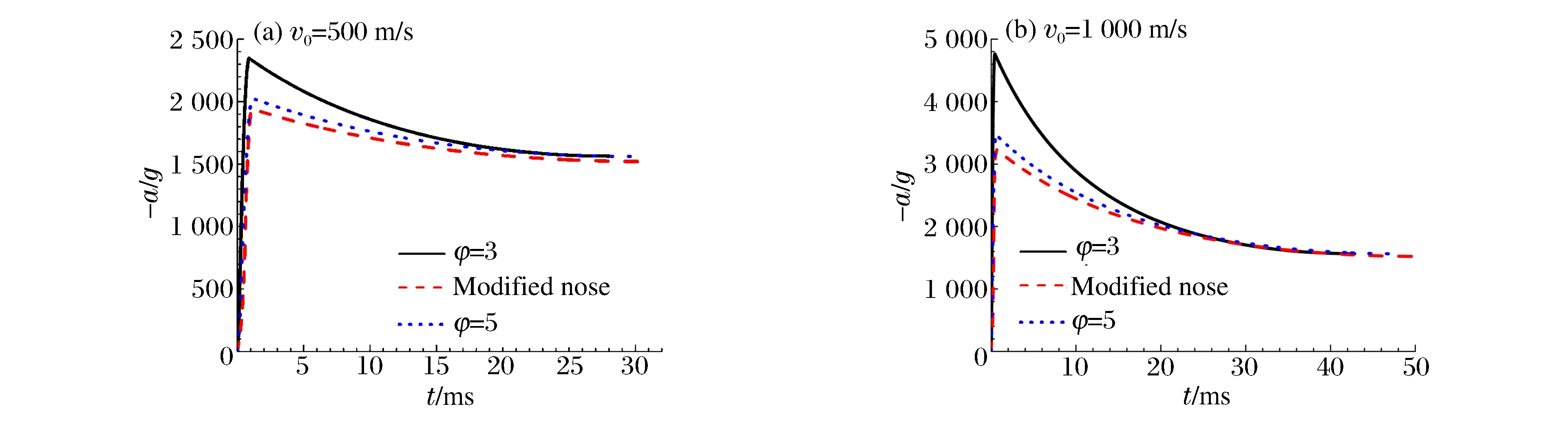
图6 侵彻体减加速度历史Fig.6 History of projectiles deceleration

图7 侵彻体侵深历史Fig.7 History of penetration depth of three projectiles

由式(6)，可得异型头部侵彻阻力：

F=F1+F2+F3=

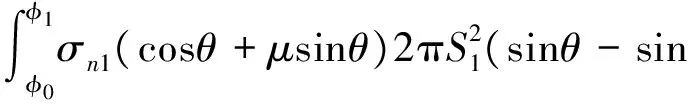
(8)

式中：σn1、σn2和σn3分别为区域1、2和3的径向应力，F1、F2和F3分别代表区域1、2和3所受阻力，μ为摩擦系数。

选取φ=3,5及双卵形异型头部3种弹体，其中异型弹体头部长度与φ=5一致，如图5所示。假设弹体为刚性，忽略侵彻过程中的头部侵蚀作用，令三者质量均为450 kg，初速度为500和1 000 m/s，靶板材料选取强度Y=35 MPa的混凝土。对侵彻特性进行数值计算，计算结果如图6～7所示。

计算结果表明，改进后的异型头部弹体在侵彻过程中所受阻力及减加速度小于φ=3和φ=5的弹体，具有更强的侵彻能力。

2 对比实验

为校核计算模型参数，验证头部系数N*对弹体侵彻阻力及侵深的影响，设计了以下对比实验[13]。选取两种卵形弹OP2与OP5，通过调整弹尾部开孔几何尺寸保证每种弹体的质量、质心一致。靶板为Y=12.8 MPa的混凝土，实验弹体特征参数见表1。

在实验研究中，伴随头部形状系数N*变化的侵深差异，是证明N*对侵深影响的有力证据，可从N*与侵深的关系中，证明上文提出的优化方案的正确性。表1中给出了几种弹体的弹体直径Dp、弹体总长Lp、头部系数N*、曲径比φ、弹体质量mp和质心距头部位置Lc，为了保证弹体质量相等，同时保证弹体重心处于弹体中部靠前位置，将弹体从后部进行不同程度的开孔。

表1也给出了两种弹体在不同速度下的3组侵彻结果：总侵深P、侵深增加ΔP和量纲一侵深增加ΔP/Dp。对于速度相近情况下的侵彻，OP5弹体侵深大于OP2，又因为两种弹体仅头部形状不同，可判断侵深差异的造成是由头部形状引起的。对头部形状系数较小的弹体OP5，其侵深大于同质量同速度侵彻下的OP2弹体。由侵深的增加量可知，侵彻速度越大时，侵深的增加量越大，即弹体头部形状对侵深的影响随着速度增加越来越明显。

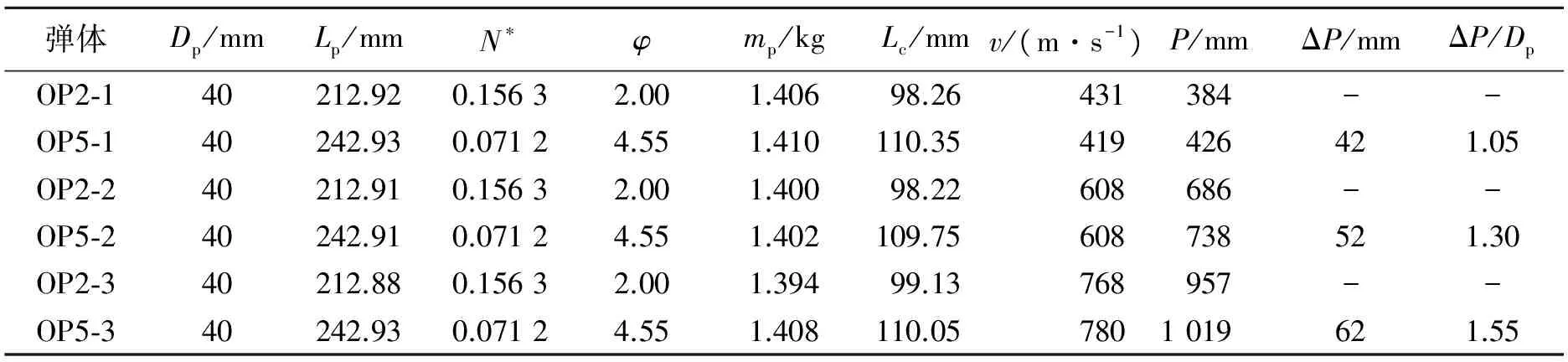
表1 弹体特征参数和侵彻结果Table 1 Characteristic parameters and penetration results of projectiles

基于前面的侵彻模型，计算了实验弹体在不同速度下的侵深曲线，图8给出了侵深的计算结果和实验结果。计算值与实验值的误差小于8%，此误差来源于靶板的非均匀性。

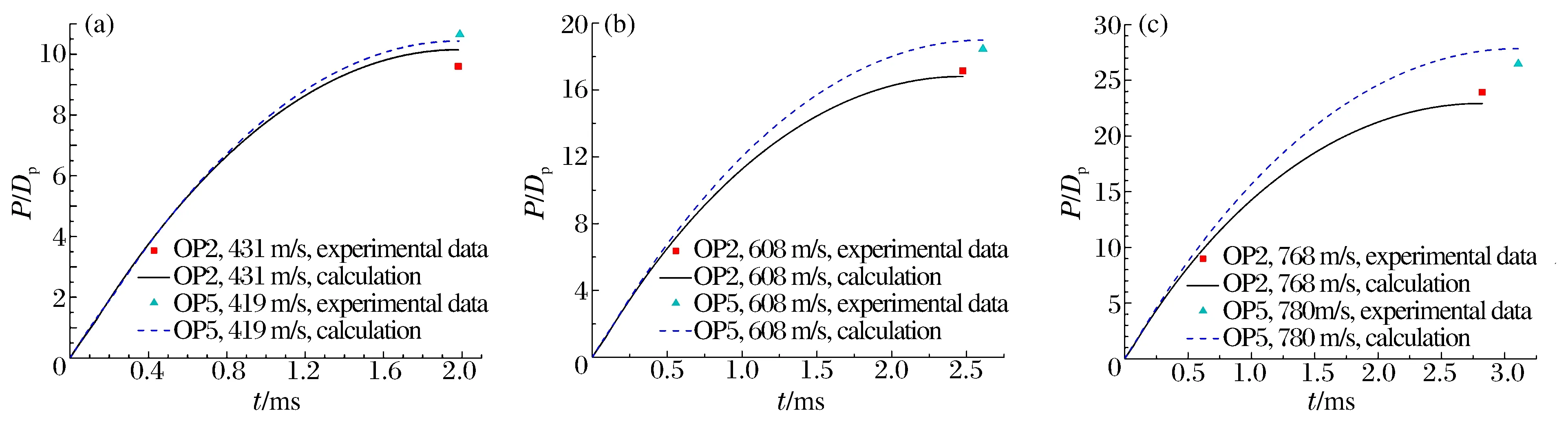
图8 两种弹体在不同速度下的量纲一侵深Fig.8 Non-dimensional penetration depth of OP2 and OP5 at the initial velocities

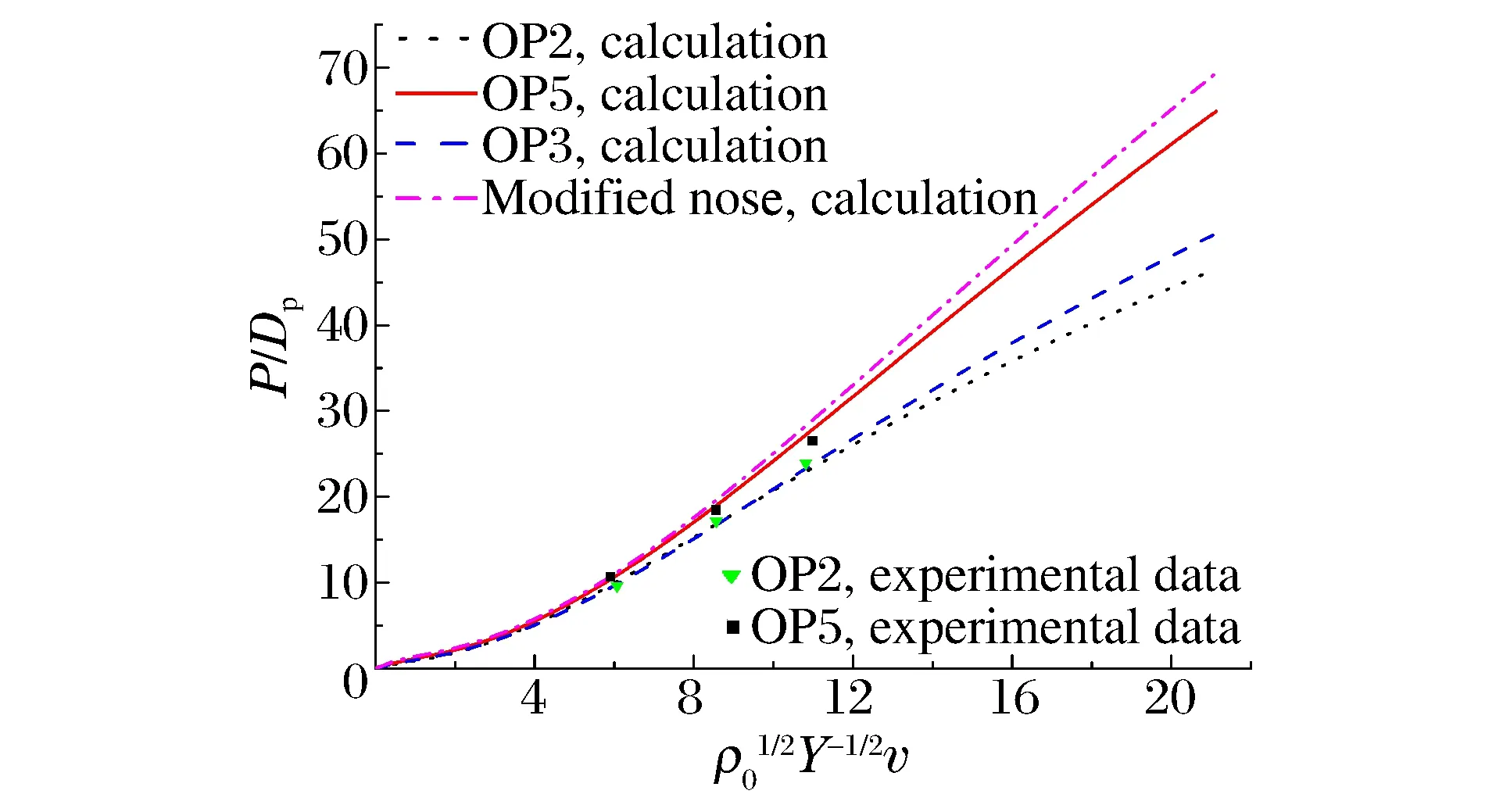
图9 4种头部弹体的量纲一侵深随初速度的变化Fig.9 Non-dimensional penetration depth of OP2, OP5, same sized OP3 and modified nose projectile versus different initial velocity

图9中对比了同弹径、同质量的OP2、OP5、异型头部及φ=3的OP3弹体在不同初速度下的侵深，同时引入实验所得的6组数据进行对比。结果表明，对头部形状系数N*较小的弹体，受到的侵彻阻力较小，最终达到的侵深较大。随着速度的提高，侵深的增量也变大。速度的提高代表侵彻过程中惯性阻力的增强，所以对惯性阻力的优化起到了重要作用。经过优化的头部可有效减小侵彻体头部形状系数N*，最终减小它所受的侵彻阻力，达到增加侵深的目的，侵深增益随侵彻着速的增加更明显。

3 结 论

(1)基于空腔膨胀理论，建立不同头部形状弹体对混凝土目标的侵彻模型，分析了弹体头部形状对弹体侵彻性能的影响规律，提出了一种双卵形异型头部结构优化设计方案。

(2)基于侵彻模型，讨论了弹体头部形状系数N*对侵彻阻力及侵彻深度的影响，由于侵彻中存在惯性阻力和静态阻力，其中惯性阻力与速度相关，而静态阻力与材料性能相关。随着速度的增加，惯性阻力项在整个阻力函数中所占比例重增加，高速侵彻的惯性阻力对侵深影响更明显。

(3)两种头部形状的侵彻实验结果表明，头部形状系数N*较小的侵彻体侵深较大，且随着速度的增加，N*对侵深的增益也增加。

(4)在同样的头部长度下，双卵形异型头部结构弹体具有比常规单卵形头部更小的头部系数N*。对文中的φ=5弹体与异型头部弹体的数值计算结果，在着速为1 000 m/s时，后者侵深提高了9.7%。

(5)异型头部对侵彻过程的影响不仅局限于惯性阻力的减小，对混凝土类脆性材料靶，具有较小直径和一定长度的异型头部前端，会对靶体产生一种预破坏效果。一定时间范围内，使侵彻体头部的中后部所受侵彻阻力，相比单卵形头部弹体大大减小。

[1] Forrestal M J, Frew D J, Hanchak S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles[J]. International Journal of Impact Engineering, 1996,18(5):465-476.

[2] Forrestal M J, Altman B S, Cargile J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994,15(4):395-405.

[3] Jones S E, Rule W K, Jerome D M, et al. On the optimal nose geometry for a rigid penetrator[J]. Computational Mechanics, 1998,22(5):413-417.

[4] Chen X W, Li Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics[J]. International Journal of Impact Engineering, 2002,27(6):619-637.

[5] Zhao J, Chen X W, Jin F N, et al. Depth of penetration of high-speed penetrator with including the effect of mass abrasion[J]. International Journal of Impact Engineering, 2010,37(9):971-979.

[6] Batra R C, Chen X. Effect of frictional force and nose shape on axisymmetric deformation of a thick thermoviscoplastic target[J]. Acta Mechanica, 1994,106(1/2):87-105.

[7] 皮爱国.大长细比动能弹体结构动态响应研究[D].北京：北京理工大学， 2007.

[8] Bishop R F, Hill R, Mott N F. The theory of indentation and hardness tests[J]. Proceedings of the Physical Society, 1945,57(3):147-159.

[9] Hill R. Cavitation and the influence of headshape in attack of thick targets by non-deforming projectiles[J]. Journal of the Mechanics and Physics of Solids, 1980,28(5):249-263.

[10] Forrestal M J, Luk V K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid[J]. Journal of Applied Mechanics, 1988,55(2):275-279.

[11] Walker J D, Anderson C E. A time-dependent model for long-rod penetration[J]. International Journal of Impact Engineering, 1995,16(1):19-48.

[12] Goldsmith W. Non-ideal projectile impact on targets[J]. International Journal of Impact Engineering, 1999,22(2):95-395.

[13] 柴传国.异型头部弹体对混凝土靶的侵彻效应研究[D].北京:北京理工大学,2014.