不同起爆方式下炸药驱动柱壳膨胀断裂的数值模拟*

刘明涛，汤铁钢，胡海波，李庆忠，胡秀章，李永池

(1.中国科学技术大学近代力学系，安徽 合肥 230027； 2.中国工程物理研究院流体物理研究所，四川 绵阳 621999)

韧性金属柱壳在高能炸药驱动下的膨胀断裂(简称外爆)是一个快速而复杂的动态过程。从炸药起爆到柱壳破坏只需数十微妙，在此过程中柱壳经受了强加载、高应变率、大变形和复杂的加卸载。

R.W.Gurney[1]给出了外爆下破片速度的经验公式并被广泛使用。G.I.Taylor[2]根据高速摄影的实验图像，提出了著名的Taylor断裂判据。C.R.Hoggatt等[3]在回收的柱壳破片内壁面附近发现了绝热剪切带，在Taylor思想的基础上，提出外爆加载下在柱壳内壁面先生成剪切带并逐步向外扩展，而后在拉应力控制下，裂纹沿着剪切带失稳面由外向内传播的破坏机制。胡八一等[4]对外爆中发生的剪切带进行了系统研究。胡海波等[5]分析了柱壳破坏中出现的“单旋”剪切现象。汤铁钢等[6]开展了一系列实验，研究柱壳破坏的应变率效应。李永池等[7]提出损伤演化方程，模拟了中心线起爆方式下柱壳的破坏过程。

实验研究中，炸药的起爆方式主要为单点起爆和平面起爆。但在理论分析和数值模拟中，多数研究按照中心线起爆处理，深入研究不同起爆方式对柱壳破裂影响的文章较少。本文中，研究这3种起爆方式对柱壳破裂的影响。

1 方 法

外爆研究中，炸药的起爆方式有3种：单点起爆、平面起爆和中心线起爆。单点起爆是指在炸药的一端插入雷管，点燃雷管引爆炸药，如图1所示。平面起爆是指炸药一端各点同时起爆，中心线起爆是指炸药柱中心线各点同时起爆。

对不同的起爆方式，金属柱壳所经受的加载历程显然不同。但无论在理论研究还是在数值分析中，为了便于理论推导和细化网格，大多忽略结构的轴向影响，把柱壳的破坏简化为二维平面应变问题，并采用中心点起爆方式起爆炸药[6-8]。这种简化对中心线起爆的柱壳中部是合理的，但大部分实验采用的是单点起爆和平面起爆[4-6]。此时这种简化是否也合理，不同的起爆方式下柱壳所经受的加载历程又有何不同？本文中将对这些问题进行相应的数值模拟，分析起爆方式对柱壳破裂的影响。

分别对3种不同的起爆方式，使用Ls-Dyna软件模拟炸药爆轰驱动柱壳膨胀的过程。为了简化计算，只计算了结构的四分之一，计算模型如图2。网格尺度为1 mm×1 mm×1 mm。

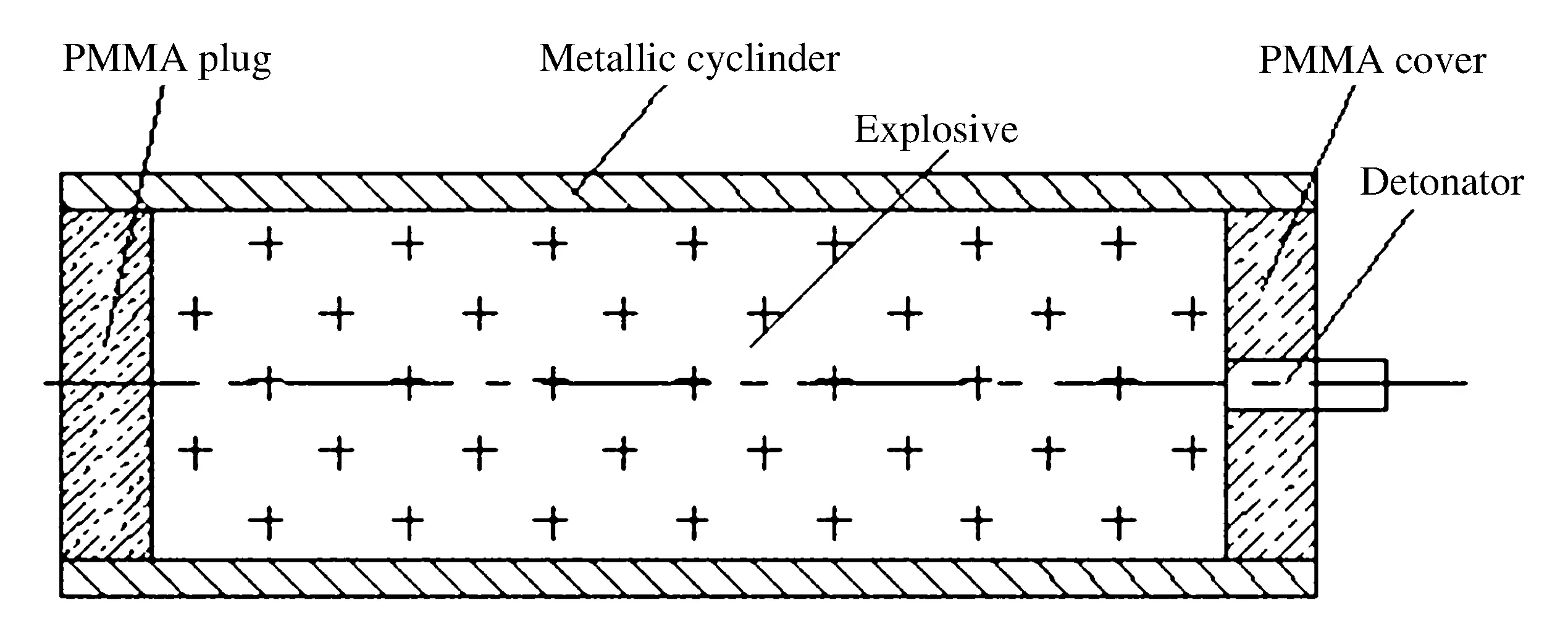
图1 实验装置示意图Fig.1 Schematic of the experimental set-up

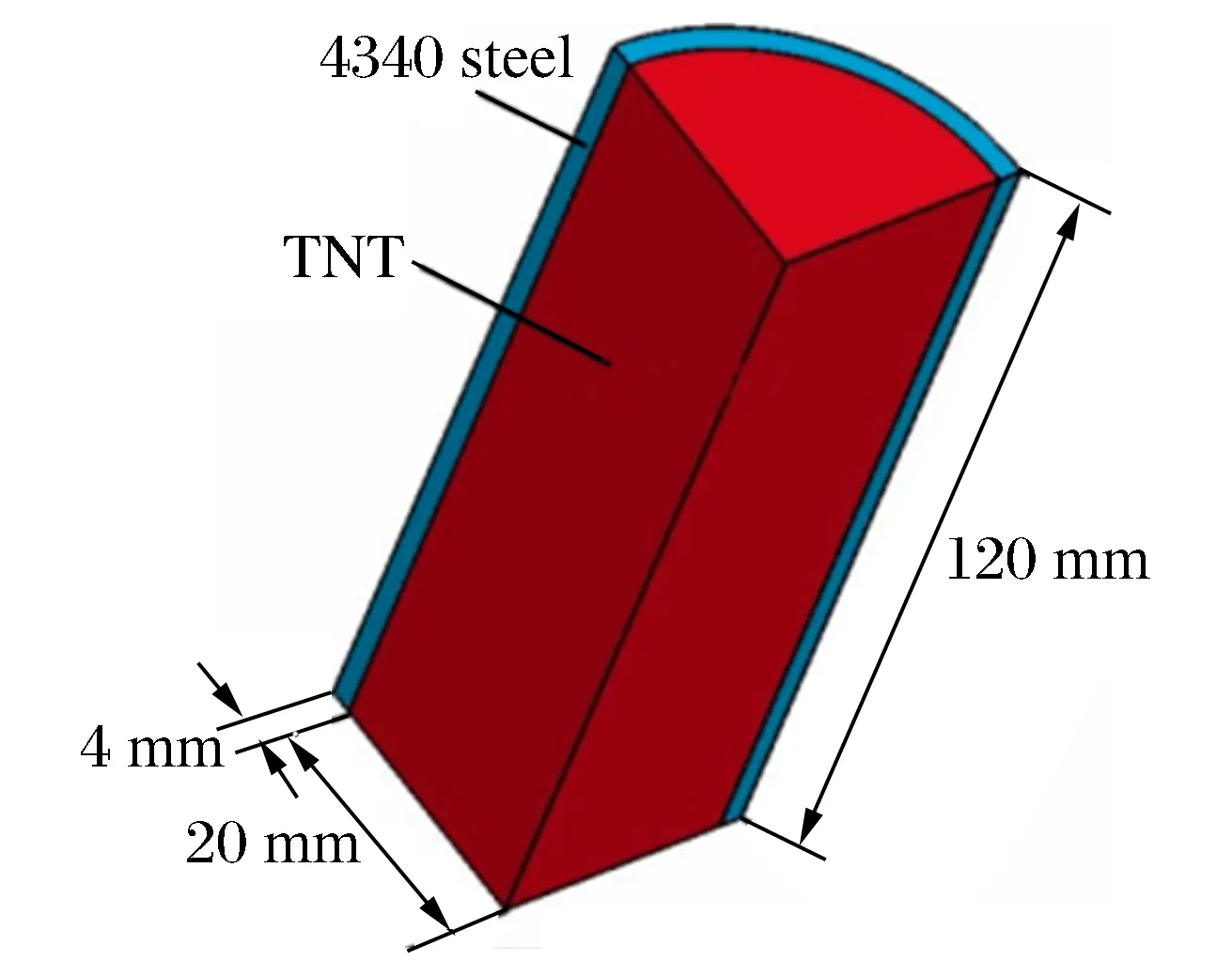
图2 数值计算建模图Fig.2 Geometry of the specimen used for simulation

金属柱壳为4340钢，强度采用Johnson-Cook模型：

(1)

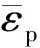
炸药为固态TNT，爆轰产物采用JWL状态方程：

(2)

式中：V为比体积，p为压力。TNT炸药的参数分别为：密度ρ=1 640 kg/m3,爆速D=6 930 m/s,爆压pCJ=27 GPa,A=374 GPa,B=3.23 GPa,R1=4.15,R2=0.95,ω=0.3。

2 结果与分析

柱壳轴向长度为12 cm，分别提取柱壳内表轴向2、4、6、8和10 cm处的径向位移曲线和爆轰产物对柱壳的压力曲线，处理数据得到炸药对柱壳内表初始单位面积的累积做功曲线。为了便于比较分析，对累积做功曲线进行平移，使爆轰产生的压力到达柱壳内表相应位置的时刻为零时刻。

2.1 平面起爆

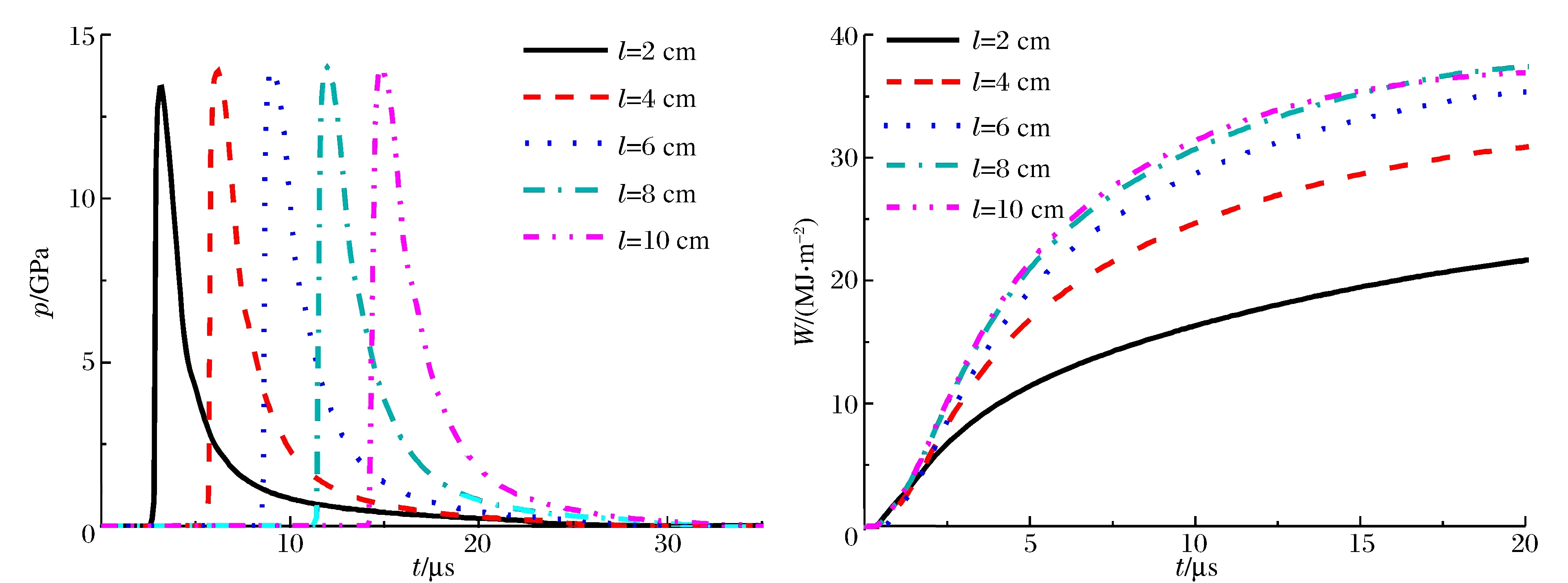
图3 平面起爆的压力和累积做功曲线Fig.3 The pressure and acting histories in planar detonation

平面起爆得到的曲线如图3所示。柱壳内表所受压力载荷峰值在2 cm处由于边界效应的影响略低，其他各处的压力峰值接近。虽然各处压力峰值接近，但卸载速度不同。接近起爆端处，直接接触空气，压力到达峰值后卸载速度快，炸药对柱壳的做功也小于远离起爆点处。在20 μs时，8 cm处的做功是2 cm处的约1.73倍。

2.2 单点起爆

单点起爆得到的曲线如图4所示。距离起爆点越远，柱壳内表所受压力载荷峰值越小。因此在初期(约2 μs以前)，做功也随距离起爆点的位置越远而越小。但是由于距离起爆点近的位置，压力卸载速度快，因此在后期，做功随距离起爆点的位置越远而越大。在20 μs时， 8 cm处的做功是2 cm处的约1.56倍。

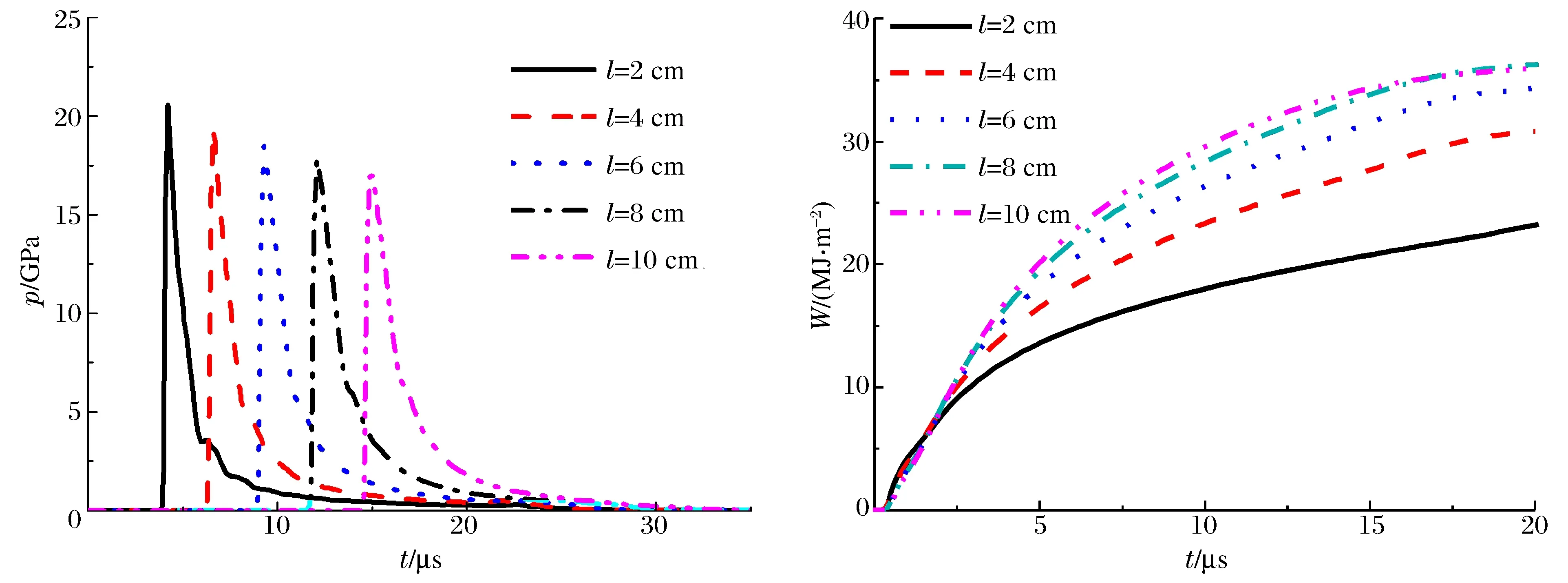
图4 单点起爆的压力和累积做功曲线Fig.4 The pressure and acting histories in point detonation

2.3 中心线起爆

中心线起爆得到的曲线如图5所示。2和10 cm处的曲线几乎重合，4、6和8 cm处的曲线几乎重合，各处的内表压力峰值接近。在6.2 μs(压力曲线中为9.0 μs)时，两侧稀疏波到达2和10 cm处，此时该两处的压力，特别是单位面积做功明显开始低于其他各处。炸药由中心线起爆后，沿径向向外爆轰，到达与柱壳的接触面，冲击波在接触面反射，向中心线会聚，而后再向外反射传播，在13.8 μs(压力曲线中为16.6 μs)时，再次到达与柱壳的接触面，二次加载柱壳。此时，压力升高，单位面积的做功也快速增加。这种重加载在平面起爆和单点起爆中没有出现。在20 μs时， 8 cm处的做功是2 cm处的约1.27倍。

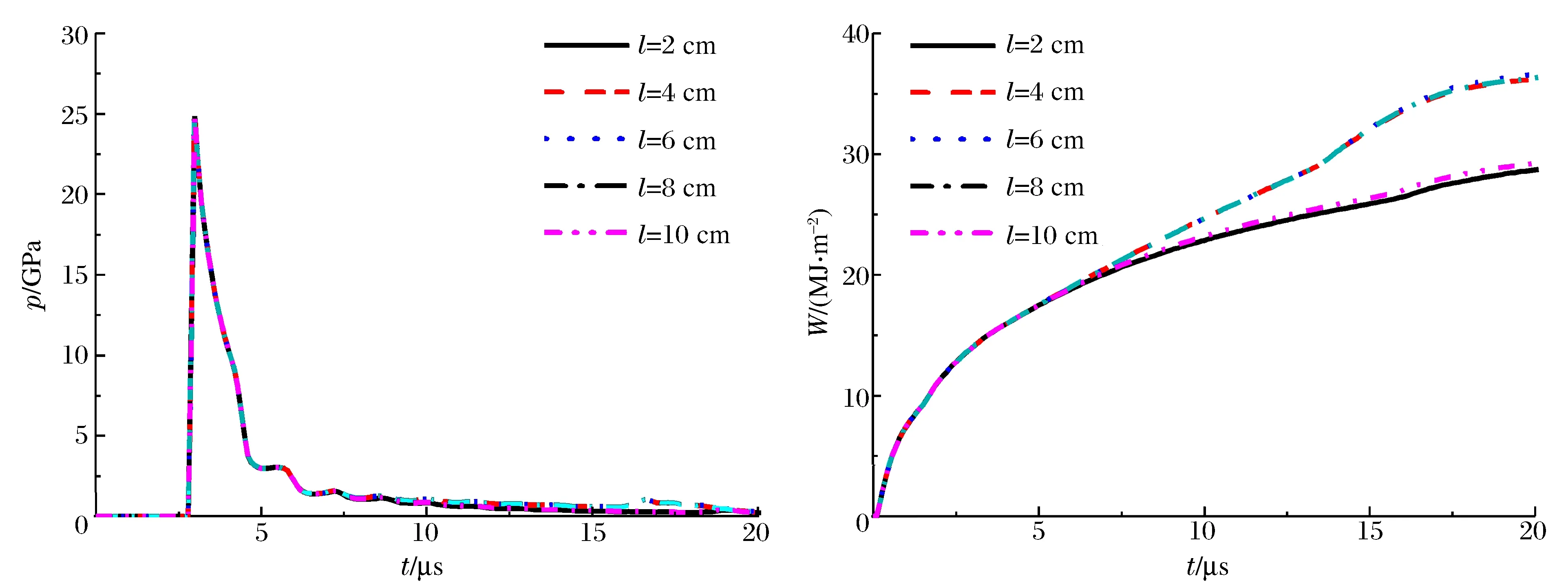
图5 中心线起爆的压力和累积做功曲线Fig.5 The pressure and acting histories in centerline detonation

2.4 不同起爆方式的差别

分别取平面起爆、单点起爆和中心线起爆下柱壳内表轴向8 cm处的数据，对比3种不同的起爆方式下爆轰气体对柱壳作用的差异，得到的曲线如图6所示。

由柱壳内表的压力曲线可以看出，不同起爆方式下柱壳内表的压力载荷历程差异显著。中心线起爆对应的压力峰值最大，其次是单点起爆，平面起爆下的压力峰值最小。达到峰值压力后，不同起爆方式下压力的卸载速度也存在明显差异，峰值压力最高的中心线起爆对应的压力卸载速度最快，其次是单点起爆，平面起爆下柱壳内表压力卸载速度最慢。根据应力波理论分析可知，该压力峰值的差别是由爆轰波对金属柱壳的入射角不同所造成的。中心线起爆方式下，爆轰波对金属柱壳正入射，爆轰波阵面平行于柱壳内表面。单点起爆和平面起爆下，爆轰波对金属柱壳均为斜入射，而平面起爆下入射角最大，因此压力峰值也最小。

从做功曲线可以看出，对轴向8 cm处的数据，在20 μs时中心线起爆比平面起爆下的做功低3.21%。即到过程末期，不同起爆方式引起的总做功差异不大。但是做功的累积过程却存在显著差异。在10 μs时，中心线起爆比平面起爆下的做功低19.5%。

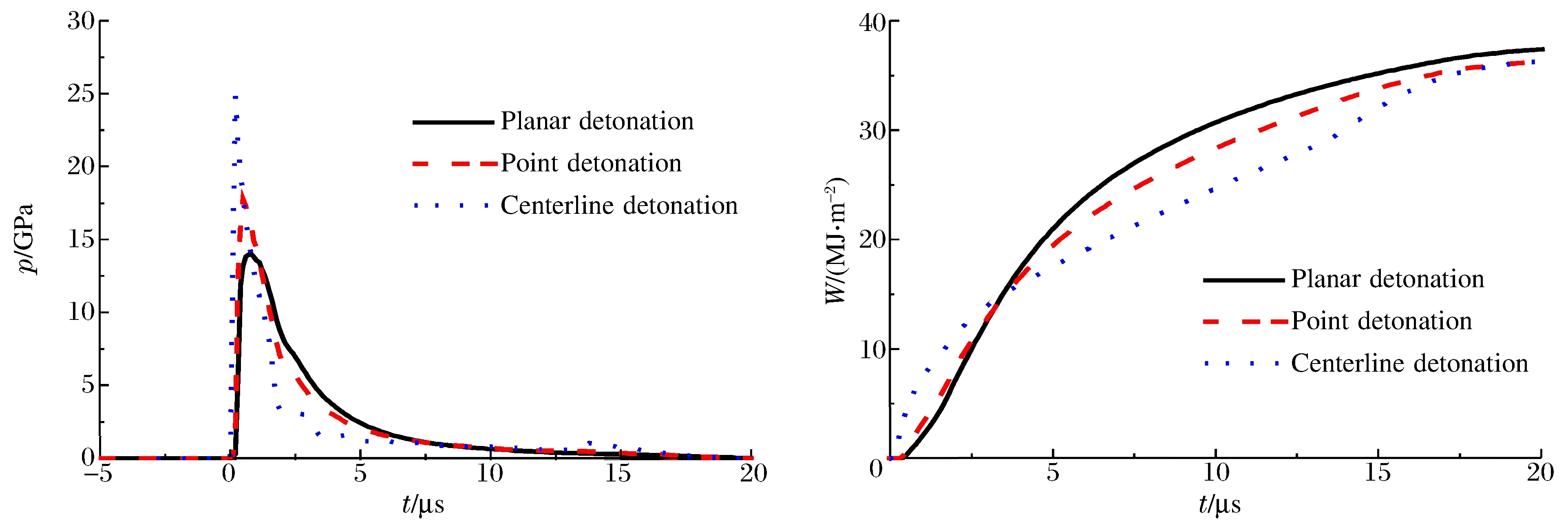
图6 不同起爆方式的压力和累积做功曲线Fig.6 The pressure and acting histories in different detonating methods

由以上分析可以看出，不同起爆方式下炸药对柱壳内表的压力、做功历史差别明显。即使同一起爆方式下，轴向不同位置的压力、做功历史也存在显著不同。因此，在数值模拟和理论分析中，必须考虑起爆方式和轴向位置的影响。

3 半解耦数值方法及分析

对外爆的数值模拟中，炸药网格占总网格的比例很大，计算效率低下[7-8]；另外，粗糙的网格划分不能描述柱壳典型破坏中出现的剪切带(实验中剪切带宽度约50 μm)，甚至不能区分两个相邻的剪切带(实验中剪切带间距约1 mm)[5-6]；此外起爆方式和轴向位置对柱壳破裂带来的影响也不容忽视。基于此，本文中提出一种炸药和柱壳计算半解耦的数值计算方法。

3.1 半解耦方法

首先，对三维模型(包括炸药和柱壳)划分较粗网格，不引入金属柱壳的破坏模型，得到爆轰产物对柱壳内表的压力曲线。然后，去除炸药，作平面应变假定进行二维计算，划分精细网格，将粗网格得到的内表压力曲线施加于柱壳内表面，同时引入金属柱壳的破坏模型。这样，一方面充分细化柱壳网格使之能模拟剪切带等破坏现象，另一方面可以准确研究不同起爆方式下柱壳不同位置的破坏。

3.2 断裂能量耗散

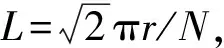
(3)

汤铁钢等[6]对图2所示尺寸的装置进行实验，使用高速摄影技术拍摄了整个膨胀过程，使用的金属材料是钢，密度ρ=7 830 kg/m3，测得剪切带间距L≈1 mm，末速度v≈1.8 km/s，单位表面积的表面能[8]约16 KJ/m2。计算得Es/Ek≈0.126%，可见断裂面的表面能所引起的能量重分配对柱壳速度的影响微乎其微，完全可以忽略不计。

3.3 柱壳膨胀断裂过程中的塑性应变能

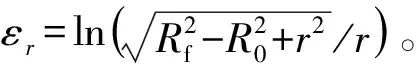
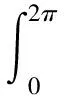
(4)

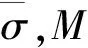
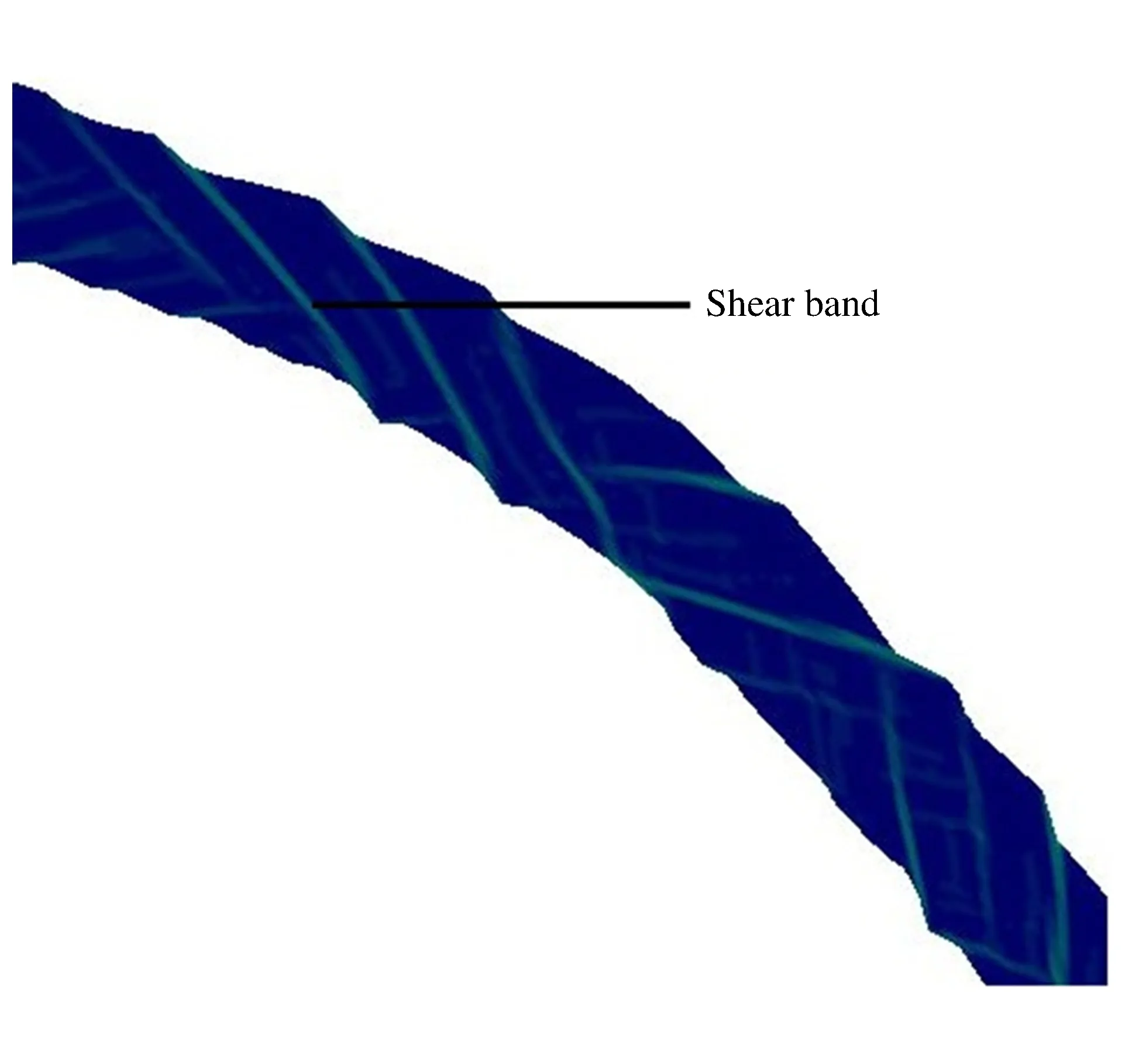
图7 半解耦法计算结果Fig.7 Modeling result using semi-decoupling method

3.4 半解耦法计算结果

对断裂耗能和塑性应变能的分析表明，破坏产生新断面的能量耗散和破坏过程中的塑性应变能对柱壳动能的影响较小，可忽略。因此半解耦数值方法是合理的，有理论依据的。采用此半解耦数值方法，模拟图2结构在单点起爆方式下轴向6 cm处壳体的破坏过程，网格尺度为90 μm×90 μm。局部放大破坏图像如图7所示，它成功地再现了炸药驱动下柱壳膨胀断裂过程中出现的绝热剪切带。

4 总 结

采用数值模拟方法，研究了3种不同起爆方式下爆轰气体产物对韧性金属柱壳内表的加载历程，发现不同起爆方式下柱壳内表所经受的压力历程差别巨大，中心线起爆峰值压力最大，单点起爆其次，平面起爆最小。理论分析认为，造成这种差别的原因是爆轰波对柱壳的入射角不同。即使在同一起爆方式下，柱壳内表轴向不同点的压力载荷历程也存在巨大差异。因此，在理论分析和数值模拟中，必须考虑起爆方式和轴向位置的影响。提出一种模拟炸药驱动下韧性金属柱壳膨胀破坏的半解耦数值方法，该方法可以实现对柱壳精细网格划分条件下的破裂模拟，并能研究不同起爆方式的影响。通过理论分析说明了这种半解耦方法的合理性。

[1] Gurney R W. The initial velocities of fragments from bombs, shell and grenades[R]. Army Ballistic Research Laboratory, 1943.

[2] Taylor G I. Fragmentation of tubular bombs[C]∥Science Papers of Sir G.I.Taylor. London: Cambridge University Press, 1963:387-390.

[3] Hoggatt C R, Recht R F. Fracture behavior of tubular bombs[J]. Journal of Applied Physics, 2003,39(3):1856-1862.

[4] 胡八一,董庆东,韩长生,等.内部爆轰加载下的钢管膨胀断裂研究[J].爆炸与冲击,1993,13(1):49-54.

Hu Ba-yi, Dong Qing-dong, Han Chang-sheng, et al. Studies of expansion and fracture of explosive-filled steel cylinders[J]. Explosion and Shock Waves, 1993,13(1):49-54.

[5] 胡海波,汤铁钢,胡八一,等.金属柱壳在爆炸加载断裂中的单旋现象[J].爆炸与冲击,2004,24(2):97-107.

Hu Hai-bo, Tang Tie-gang, Hu Ba-yi, et al. An study of uniform shear bands orientation selection tendency on explosively loaded cylindrical shells[J]. Explosion and Shock Waves, 2004,24(2):97-107.

[6] 汤铁钢,李庆忠,孙学林,等.45钢柱壳膨胀断裂的应变率效应[J].爆炸与冲击,2006,26(2):129-133.

Tang Tie-gang, Li Qing-zhong, Sun Xue-lin, et al. Strain-rate effects of expanding fracture of 45 steel cylinder shells driven by detonation[J]. Explosion and Shock Waves, 2006,26(2):129-133.

[7] 李永池,李大红,魏志刚,等.内爆炸载荷下圆管变形、损伤和破坏规律的研究[J].力学学报,1999,31(4):442-449.

Li Yong-chi, Li Da-hong, Wei Zhi-gang, et al. Research on the deformation, damage and fracture rules of circular tubes under inside-explosive loading[J]. Acta Mechanica Sinica, 1999,31(4):442-449.

[8] 黄西成.内爆与外爆加载下壳体的力学状态及破坏模式分析[D].绵阳:中国工程物理研究院,2010.