汽车悬架系统中铰接点载荷的计算方法*

上官文斌，代 林，林浩挺，俞 宏

(1.华南理工大学机械与汽车工程学院，广州 510641； 2.宁波拓普集团股份有限公司，宁波 315800)

前言

控制臂(control arm，也称摆臂)是汽车悬架系统中的导向和传力元件[1]。控制臂往往通过衬套与车身相连，而通过球铰或衬套与转向节相连。作用于车轮上的各种载荷，通过转向节臂-球铰(或衬套)-控制臂-衬套，将力传递给车身。同时，在这些力的作用下，衬套发生变形导致控制臂运动，进而改变车轮的运动轨迹。为确保汽车行驶的安全性和操纵稳定性，控制臂应具有足够的强度、刚度和使用寿命。

目前对控制臂的断裂、疲劳失效等问题的优化设计，主要采用有限元分析和试验[2-4]相结合的方法，其中，疲劳破坏的载荷的频率都很低。对控制臂进行疲劳分析时，一般都采用准静态的载荷加载。实际上，无论是进行控制臂的有限元分析，还是进行控制臂的拉伸、压溃和冲击试验，均须确定作用在控制臂各球铰和衬套的力，作为计算与试验的载荷。

由汽车各行驶工况(通用公司规定为29种工况)，可确定作用在车轮上的载荷，进而求出作用在控制臂球铰和衬套上的载荷。文献[5]中介绍了一种简化的双横臂悬架系统模型，把控制臂与车身铰接处简化为一个球铰和一个内联约束(inline joint primitive constrain)，建立线性方程组来计算悬架系统受力。计算结果表明，该方法对计算控制臂与转向节相连球铰的受力较为准确，但是不能准确计算出控制臂与车身铰接处的受力大小。文献[6]中以麦弗逊悬架系统为例，将衬套等效为具有三向线刚度的弹簧，采用位移矩阵法求得各铰接点的力。该方法对计算典型工况下各铰接点的受力是有效的，但由于忽略了衬套的扭转刚度和衬套刚度的非线性特性，当汽车在一些极限工况下运行时，该方法不能准确计算出控制臂与车身铰接处以及各衬套的受力情况。

本文中以双横臂悬架系统为例，研究了悬架系统中铰接点载荷的计算方法：建立了悬架系统的铰接点载荷计算的模型和悬架系统力-位移静平衡方程，给出了悬架系统球铰力和衬套力的计算公式。建模中，将衬套简化为具有3个互相垂直方向的线刚度和绕这3个方向扭转刚度的模型，同时考虑了衬套在各个方向的非线性特性。针对一双横臂悬架系统，利用未考虑控制臂衬套弹性的模型、仅考虑控制臂衬套弹性线刚度的模型及同时考虑衬套非线性线刚度和非线性扭转刚度的模型(本文中提出的模型)，计算了在汽车运行的典型工况和极限工况下，悬架系统各铰接点的受力。计算结果表明，当悬架系统受到一些极限工况作用时，考虑衬套六向非线性刚度的模型能更准确地计算出悬架系统各铰接点的受力大小。本文中的建模与计算方法和计算结果，可用于确定悬架系统控制臂疲劳试验载荷和强度计算时的输入载荷。

1 悬架系统建模与载荷计算方法

1.1 悬架系统模型

本文中以双横臂悬架系统为例论述悬架系统的建模方法。图1为双横臂悬架系统简化模型，它由上、下控制臂，车轮与转向节，弹簧与减振器，以及转向横拉杆连接而成[5]。上、下控制臂的一端分别通过衬套1、2、3和4与车身相连，另一端分别通过球铰D和G与转向节相连；车轮与转向节刚性连接，视为一个刚体；弹簧与减振器通过球铰I和C分别与车身和控制臂体相连；转向横拉杆一端由球铰J与转向器相连，另一端则由球铰H与转向节相连。

为了建模方便，衬套i(i=1,…,4)表示位于点A、B、E和F处的衬套；铰接点Ni表示与衬套i所在控制臂同转向节相连接的铰接点。由图1中的悬架系统知，衬套i(i=1,2,3,4)对应的铰接点Ni处于D或G点。建立悬架系统载荷计算的模型时，进行如下假设[7-8]：

(1) 除衬套和弹簧外，悬架系统中各元件均为刚体，不存在变形；

(2) 忽略悬架系统各元件的重力和各球铰铰接处摩擦力的影响；

(3) 在汽车的各种行驶工况下，悬架系统的受力为准静态过程，即不考虑各工况下的惯性力和阻尼力。

1.2 弹性衬套模型

为衰减汽车高速行驶引起的振动和冲击，悬架系统控制臂通过弹性衬套与车身相连[9]。在已发表的文献中，通常将衬套简化为在其局部坐标系3个垂直的弹性主轴方向(u、v、w)具有线刚度的元件，未考虑其扭转刚度[6]。本文中扩展了已有的衬套模型，除线刚度外还计及扭转刚度。其中，3个线刚度记为kt,u、kt,v和kt,w，3个扭转刚度记为kr,u、kr,v和kr,w，如图2所示。

弹性元件的力-位移关系一般为非线性，采用图3所示的5个分段线性表征其非线性特性，该方法在动力总成悬置系统位移控制计算中得到了应用[1,10]。衬套在任一方向的力F(力矩M)和位移x(角度θ)的力-位移非线性特性的数学表达式为

F=kx+Δ

(1)

式中：x为衬套的平动位移或转动角度；Δ为位移在非线性段的位置时，力-位移关系曲线的修正项。若变形量x不同，k和Δ不同，其计算公式见文献[1]和文献[10]。

1.3 悬架系统载荷的计算方法

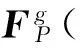
悬架系统在控制臂受到弹性元件的力和车轮与转向节臂受到地面反力的共同作用下，达到静平衡状态，可列出悬架系统的静平衡方程。由转向横拉杆的长度不变，及减振器弹簧长度的变化关系，可得悬架系统的几何约束方程。这样，由悬架系统的静平衡方程和几何约束方程，建立了悬架系统载荷计算的约束方程组。求解该方程组，可算得某一工况下悬架系统各球铰和各弹性衬套的受力。

2 悬架系统载荷计算方程的建立

2.1 控制臂静平衡方程

2.1.1 控制臂衬套受力计算

在车轮接地点力的作用下，衬套产生弹性变形，由此产生了平动位移和转动位移，使衬套安装点发生变化。变化后，衬套i(i=1,2,…,4)在整车坐标系og-xgygzg下的新坐标Si*为

Si*=T(Si-Ni)+Ni*

(2)

式中：T为坐标转换矩阵[5]，Si为衬套i的初始安装点坐标，是3×1的向量。Ni和Ni*分别为衬套i(i=1,2,…,4)所在的控制臂同转向节相连接的铰接点Ni的初始坐标和新坐标。

(3)

(4)

(5)

2.1.2 控制臂静平衡方程

安装有减振器弹簧的控制臂，在弹性元件(衬套和弹簧)反力和转向节对控制臂作用力的共同作用下处于静平衡。对铰接点Ni取力矩平衡方程，可得控制臂在整车坐标系og-xgygzg下的静平衡方程为

(6)

(7)

2.2 转向节静平衡方程

在控制臂与转向横拉杆对转向节的作用力和车轮接地点的反力作用下，转向节处于静平衡。对车轮接地点P取力矩平衡方程，可得转向节在整车坐标系og-xgygzg中的静平衡方程为

(8)

2.3 悬架系统几何约束方程

(9)

(10)

2.4 双横臂悬架系统载荷计算方程

式(6)～式(10)给出了悬架系统中载荷计算的一般方程。将铰接点D或G代替式(2)～式(8)中变量下标含Ni的位置，可得到该双横臂悬架系统中铰接点载荷计算的约束方程为

(11)

3 约束方程的求解

(12)

Am+1=Am+(zm-Amym)(ym)T/‖ym‖

(13)

式中：x为具有n个未知数的向量；m为第m步迭代；Am非奇异；ym=xm+1-xm；zm=F(xm+1)-F(xm)。

预位移的计算方法：求汽车自重作用下衬套预位移时，各衬套在弹性主轴方向的变形处于线性范围[b,c]内，且式(1)中的位移修正项Δ=0。求解各衬套预位移的步骤如下：

(1) 假设衬套预位移为0，以此作为衬套位移初始值；

(2) 利用式(11)迭代求解，可得控制臂和转向节的转动角度及D点的新坐标。利用式(3)，计算汽车自重下衬套在各个方向的位移。记录本步得到的衬套位移，作为步骤(3)计算时的衬套位移初始值；

(3) 重复一次步骤(2)的计算过程，得到新的衬套位移。

检查步骤(3)和步骤(2)中计算出的衬套位移的差值是否小于指定值。若是，则停止计算，将步骤(2)中的衬套位移作为汽车自重作用下衬套预位移。否则，重复步骤(2)和(3)，将步骤(3)计算得到的位移，作为重复步骤(2)的衬套位移初始值。

通过步骤(1)～步骤(3)的计算，可得到在汽车自重作用下衬套预位移。

求解某一工况下衬套受力和力矩时，衬套刚度k和力-位移修正项Δ是由衬套的位移确定的。详细求解的迭代过程见文献[1]和文献[10]。

4 计算实例与分析

以某汽车右前轮双横臂独立悬架系统为计算实例。根据悬架系统约束方程(11)，计算出在典型工况和极限工况下双横臂悬架系统各球铰和各衬套的受力。

4.1 双横臂悬架系统与衬套参数

表1 双横臂悬架系统各点坐标

表2 衬套在其局部坐标系的线刚度和拐点值

表3 衬套在其局部坐标系的扭转刚度和拐点值

4.2 不同悬架系统模型计算结果对比

按照文献[5]中的方法，将悬架系统的控制臂通过球铰和内联约束与车身刚性地连接在一起，定义该模型为模型I。按照文献[6]中的方法，控制臂衬套等效为具有三向线刚度的弹簧，定义该模型为模型II。本文中建立的悬架系统模型同时考虑衬套的线刚度和扭转刚度，且均为非线性，定义为模型III。

为了对比在不同工况下，采用模型I、II和III时，悬架系统各球铰和各衬套受力计算结果的差异，本文中选取两种典型工况和两种极限工况进行计算。其中，模型III的计算结果均预先通过ADAMS模型的仿真结果进行了对比，验证了其计算结果的正确性和有效性。

4.2.1 典型工况

典型载荷工况如表4所示。工况1为车辆前进时以0.5g的减速度制动；工况2为车辆以0.6g的侧向加速度弯道行驶。两种工况下，利用3种不同的悬架系统模型，计算得到各铰接点的受力见表5和表6，控制臂各衬套的受力和力矩见表7和表8。

表4 典型载荷工况 N

从表5和表6的计算结果可以看出，在典型工况下，利用模型I计算得到的球铰D和G的受力与利用模型III计算出来的结果接近。模型I中，由于将控制臂上与车身相连的铰接点(A、B、E和F)简化为刚性连接，因此这些铰接点计算结果与模型III的计算结果差别较大，尤其是x方向；而利用模型II和模型III计算得到各铰接点的力基本一致。

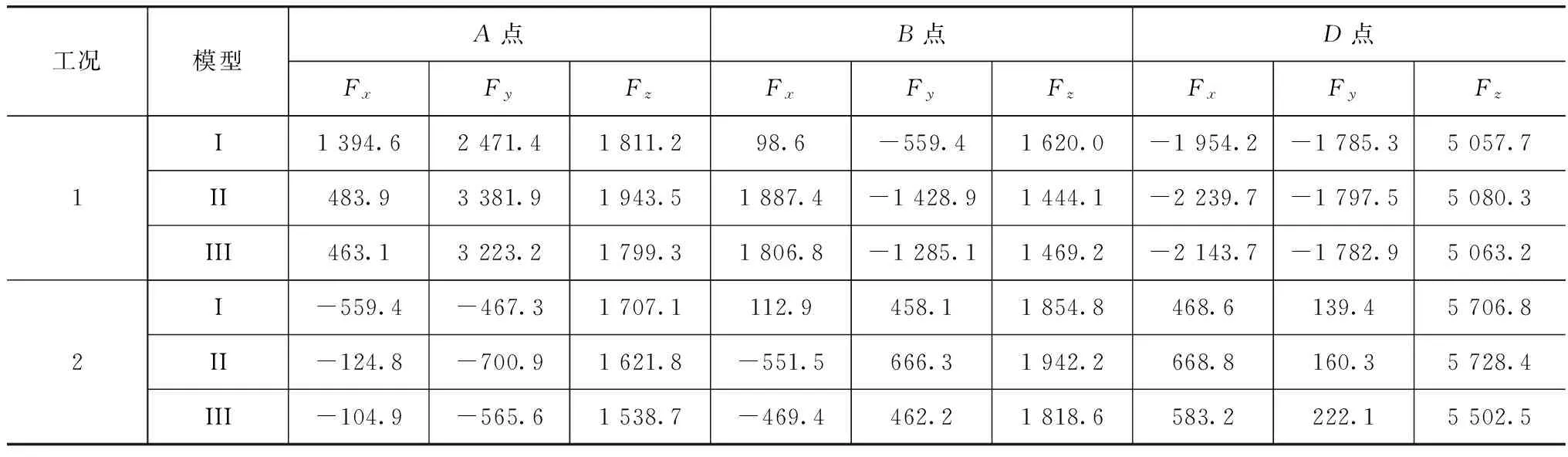
表5 典型工况下，上控制臂铰接点的受力 N

表6 典型工况下，下控制臂铰接点的受力 N

表7 典型工况下，上控制臂衬套的受力和力矩

表8 典型工况下，下控制臂衬套的受力和力矩

由以上计算结果的分析表明，在典型工况下，为了精确分析控制臂上铰接点的受力，应采用模型II或模型III。

从表7和表8的计算结果可以看出，在典型工况下，利用模型II计算得出的控制臂各衬套的受力与利用模型III计算得出的结果基本一致。计算结果表明，在典型工况下，模型II和模型III均能准确计算控制臂各衬套的受力情况；而模型III能同时反映出各个衬套所受的力矩，更准确地模拟衬套的工作情况。

4.2.2 极限工况

极限载荷工况如表9所示。工况3为车辆以1g的侧向加速度发生侧翻；工况4为车辆前进时以1g的减速度制动。

表9 极限载荷工况 N

在表9所列两种工况下，利用3种不同模型计算得到各铰接点载荷见表10和表11，控制臂各衬套力和力矩见表12和表13。

从表10和表11的计算结果可以看出，在极限工况下，利用模型I，II，III在计算控制臂铰接点受力时，各向受力均相差较大，其中x向受力大小差别尤为明显。计算结果表明，在极限工况下，利用模型III能更准确地计算出控制臂各铰接点的力。衬套对控制臂各铰接点的受力有很大的影响，衬套扭转刚度在较大程度上影响着控制臂各铰接点的受力大小分配，不可忽略。

表10 极限工况下，上控制臂铰接点的受力 N

表11 极限工况下，下控制臂铰接点的受力 N

表12 极限工况下，上控制臂衬套的受力和力矩

表13 极限工况下，下控制臂衬套的受力和力矩

从表12和表13的计算结果可以看出，在极限工况下，利用模型II和模型III在计算衬套受力时，各方向的受力相差较大。同时，模型III考虑了衬套的扭转变形，可以计算出衬套所受到的转矩大小，且模型III衬套受力计算结果与模型II的计算值相比要偏小。这也从另外一个角度论证了文献[11]中的研究结论：优化衬套的刚度可以提高控制臂的耐久性。

由以上计算结果的分析表明，在极限工况下，利用模型III能更准确地计算出控制臂各衬套的力和力矩。衬套的扭转刚度对各个铰接点载荷的影响较大，因此考虑扭转刚度的衬套模型，能更加准确地反映衬套对铰接点冲击力的减缓作用。

5 结论

(1) 考虑了衬套在6个自由度的非线性刚度，建立了悬架系统各球铰和各衬套受力计算的模型和计算方法，给出了悬架系统各球铰力和衬套力的计算公式。

(2) 通过对一双横臂悬架系统中球铰和衬套的受力计算与对比分析表明：与不考虑衬套弹性的悬架系统模型和仅考虑衬套三向线刚度的悬架系统模型相比，本文中所建立的悬架系统模型考虑了衬套的三向非线性线刚度和三向非线性扭转刚度，更加准确地反映出汽车在各种工况下悬架系统各铰接点的受力状况，算出的载荷更加精准地表征了控制臂的实际载荷。

(3) 在极限工况下，衬套的扭转刚度对悬架系统中铰接点载荷分配的影响比典型工况时大，不能忽略。

(4) 计算得到各铰接点的载荷为优化悬架系统中的衬套、控制臂和球铰提供了计算和疲劳试验的载荷。

[1] Tang L, Shangguan W B, Dai L. A Calculation Method of Joint Forces for a Suspension Considering Nonlinear Elasticity of Bushings[J]. I. Mech. E. Part K: J. Multi-body Dynamics,2012,226(4):281-297.

[2] 上官文斌,蒋翠翠,潘孝勇.汽车悬架控制臂的拓扑优化与性能计算[J].汽车工程,2008,30(8):709-712.

[3] Miguel A E, Huang M, Tyan T. Impact Testing of Lower Control Arm for Crashworthiness Simulation[C]. SAE Paper 2005-01-0352.

[4] Huang M, Miguel A E, Tyan T. Crashworthiness Simulation of Lower Control Arm Impact Tests[C]. SAE Paper 2005-01-0361.

[5] Blundell M, Harty D. The Multibody Systems Approach to Vehicle Dynamics[M]. New York: Elsevier Butterworth- Heinemann,2004.

[6] Suh C H. Joint Force and Moment Analysis of a Three-Dimensional Suspension Mechanisms[C]. SAE Paper 910015.

[7] Knapczyk J, Dzierzek S. Displacement and Force Analysis of Five-Rod Suspension with Flexible Joints[J]. ASME Journal of Mechanical Design,1995,117(4):532-538.

[8] Sohn J H, Yoo W S, Hong K S, et al. Massless Links with External Forces and Bushing Effect for Multibody Dynamic Analysis[J]. Journal of Mechanical Science and Technology,2002,16(6):810-818.

[9] Ledesma R, Ma Z D, Hulbert G, et al. A Nonlinear Viscoelastic Bushing Element in Multibody Dynamics[J]. Computational Mechanics,1995,17(5):287-296.

[10] 上官文斌,徐驰,黄振磊,等.汽车动力总成悬置系统位移控制设计计算方法[J].汽车工程,2006,28(8):738-742.

[11] Kang B J, Kim N W, Kim J H, et al. Improving the Durability of Automobile Suspension Systems by Optimizing the Elastomeric Bushing Compliance[J]. I. Mech. E. Part D: J. Automobile Engineering,2008,222:468-484.