汽车热管理瞬态分析与应用

陈鸿明，武亚娇，华益新，杨雪松

(泛亚汽车技术中心有限公司，上海 201201)

前言

目前国内较多整车热管理仿真计算是针对稳态工况进行，采用的方法是依据稳态分析结果再加上一些工程经验对整车热性能做出整体判断[1-2]，而对于某些较为复杂的瞬态工况(例如发动机怠速和熄火之后的过程)并不能进行合理的评估[3]，导致无法在开发前期准确预测该零件的耐热特性是否满足设计要求。零件承受的温度和在该温度下所经受的时间是制约零件使用寿命的两个关键因素，所以整车热分析不仅要计算出零件可能承受的温度，同时也要准确推断出在该温度下能正常工作的时间，这样才能准确计算出零件在整车上的使用寿命。本文中采用瞬态热分析软件RadTherm，对车辆在经历恶劣工况后的熄火过程进行瞬态仿真计算，准确模拟出该过程受热零件的温度变化和持续时间，从而为零件的使用寿命评估提供依据。

1 瞬态工况计算方法

1.1 瞬态工况

本文中所描述的瞬态工况类似在山路上的爬坡过程，即以某一稳定速度爬过固定坡度的坡道，然后熄火停车。在此过程中，匀速爬坡行驶时，发动机前舱主要的传热方式为强迫对流换热和辐射传热，冷却风扇处于最高转速状态；当发动机熄火时，前舱空气流动转为自然对流换热和辐射传热，冷却风扇处于关闭状态，此时，发动机前舱内排气管温度不会瞬间降低，而是有一个缓慢降温的过程。在这个过程中其周围零件受到来自排气管的持续烘烤，而没有强迫对流对其进行冷却，零件温度会在短时间内急剧升高，并持续一段时间之后才会下降。由于各零件与排气管的距离和本身材料属性的不同会导致各个零件的温升数值和持续时间不同，RadTherm主要是对此温升过程进行仿真计算，得到受热零件的温度变化曲线，从而根据零件的温度要求来判断该零件在温升过程中是否能满足设计要求。

图1为某一前舱零件在进行整车热性能试验之后的温度曲线。从图中看出，该零件在爬坡过程中温度没有超过其材料自身温度限值，但在熄火之后，温度超过温度限值并持续一段时间，零件这种超过耐温限值的状态称为热疲劳状态，长时间处于这种状态会导致零件失效，影响车辆行驶安全。因此采用RadTherm软件在开发前期对可能遇到的恶劣工况进行仿真分析计算，确定零件耐温特性是否满足整车热性能要求就显得非常重要。

1.2 RadTherm计算理论[4]

RadTherm通过求解能量方程和热辐射封闭方程得出控制方程。首先，RadTherm遵循热力学第一定律，能量在转化和传递过程中总和不变，有

(1)

式中：E为系统内能；Q为热量。

将式(1)展开可得到

(2)

式中：m为节点质量；T为节点温度；Cp为材料的等压比热容；Qconv、Qcond和Qrad分别为节点通过热对流、热传导和热辐射3种传热方式所吸收的热量；Qimposed为节点所吸收的外部热源(如太阳能或者电能)热量。用传热学理论将Qconv和Qcond展开，可得k节点的瞬态能量方程为

Qradk+Qimpk

(3)

式中：hk为对流换热系数；Ak为接受对流换热和热传导的面积；Tf为周围流体的来流温度；kkj为材料的热传导系数；Akj为k节点与j节点之间的接触面积；Lkj为k节点和j节点之间的距离。Qradk为辐射项，可从热辐射的封闭方程获得,假设物体为灰体，辐射方式为漫反射，参与辐射的物体表面为N，那么热辐射的封闭方程为

(4)

式中：εj为j节点面的发射率；Fk-j为从k节点面到j节点面的角系数；σ为斯蒂芬-波尔兹曼常数；Aj为节点面面积；δkj为克罗内克函数。由式(4)求解Qk：

(5)

Qk项为k节点面的辐射损失,和式(3)中的-Qradk相等。将式(3)中的Qradk用-Qk代替可得

(6)

式(5)和式(6)就是RadTherm软件求解温度分布的控制方程。

1.3 RadTherm计算瞬态工况[5]

本文中计算的瞬时工况从匀速爬坡开始，直到发动机熄火之后一段时间结束，计算过程见图2。工况1是匀速爬坡的开始(t=0)；工况2是匀速爬坡经过30min运行结束(t=30min)，工况2′是熄火状态的开始(t=30min+步长)，工况2和工况2′在实际状态应该是同一点，但因计算中须设置边界条件，故将二者之间用一个时间步长隔开；工况3是熄火的终止状态(t=50min)，这4个工况车辆和冷却风扇状态见表1。

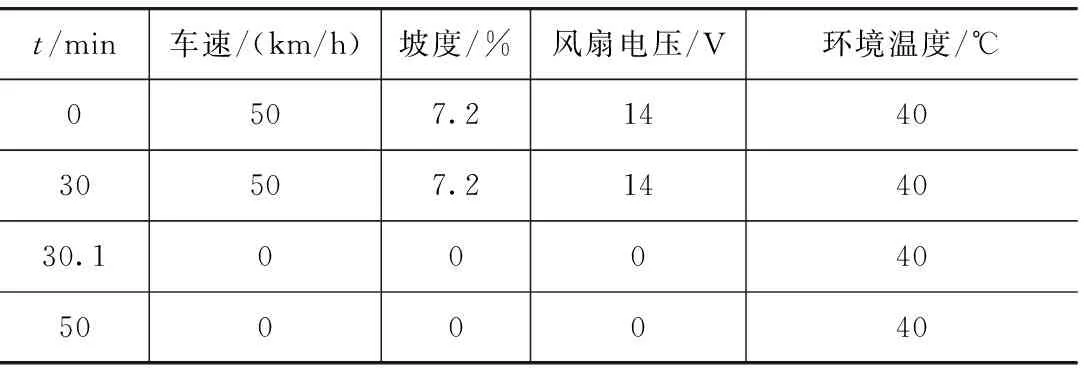
表1 不同工况的车辆行驶和风扇转动状态

这4个工况点均是以Fluent计算的稳态流动换热系数和流体温度作为RadTherm瞬态计算的边界条件，在工况2′和工况3两个时刻之间排气管的温度在缓慢下降，如果只导入工况2′和工况3的边界，RadTherm只会对导入的稳态数据进行线性插值，得到的计算结果会与实际差别较大。本文中在这两个工况点之间插入3个耦合计算的工况点，使排气管温度变化过程和零件周围的边界条件更加符合实际状态。

2 模型建立

2.1 网格模型建立

基于某四缸缸内直喷发动机轿车建立数学模型，主要包括发动机前舱离排气歧管较近的零件和车辆底盘排气管附近的零件。模型的建立分为两部分，一部分用于Fluent稳态计算，另外一部分用于RadTherm瞬态计算。具体模型见图3。稳态计算模型大概包括120个零件，90万三角形面网格单元；瞬态计算提取发动机前舱距离隔音棉较近的排气管和隔音棉作为研究对象。

2.2 RadTherm计算边界条件

计算边界条件包括两部分，一部分是通过Fluent计算得到稳态流动换热结果作为边界条件，其中稳态计算的边界条件主要有排气流量、温度和环境温度，另一部分为各个零件材料本身的参数设置。本文中主要研究瞬态计算，所以关于稳态计算的参数设置不予详述。在这里要特别提出的是零件材料的反射率和吸收率的设定，反射率和吸收率不仅与材料本身有关，且与零件表面的氧化程度也有很大关系。所采用的各种材料反射率和吸收率均来自于公司内部材料数据库，根据车辆的使用情况和零件的氧化程度选择对应的反射率和吸收率。

稳态计算结束后，从Fluent软件导出所需数据作为RadTherm瞬态计算的初始边界条件，导出结果主要包含与各个零件表面相接触的流体温度和零件表面的热交换系数等。零件的材料属性需要重新设置，主要有热传导率、反射率、吸收率和材料厚度等。需要特别注意的是发动机排气管和内部气体的边界设置，图4给出内部气体温度和流量曲线。排气流量在发动机熄火后降为零，但是排气管表面和内部气体的温度并不会立刻冷却下来，通过耦合计算得出排气管表面和内部气体温度的缓慢降温过程作为瞬态计算的最终边界条件[6]。

3 瞬态工况分析结果

3.1 验证仿真的可行性

通过RadTherm的瞬态计算与试验数据进行比较，进而验证仿真的准确性。图5给出隔音棉上测点仿真和试验结果的对比。由图可见，仿真结果比试验结果温度要高，主要原因在于Fluent稳态计算给定的排气温度边界条件比实际测量温度高，导致仿真结果数值比试验结果偏高。另外，从第30min开始(即熄火开始)，1点和3点仿真结果和试验结果吻合较好，主要是由于当发动机熄火后，经过耦合计算后得出的排气管温度边界准确度较高，使仿真结果更加接近试验值。但是2点的仿真结果和试验结果相差20℃，主要原因在于，2点附近有制动管和空调管等一些直径较小的管路，在建模初期，未建立这些管路模型，导致仿真过程中此处附近对流换热情况比实际情况好，所以仿真结果的温升没有试验结果的高。

综合比较RadTherm仿真结果和试验数据之后，可以得到以下结论：一方面，如果能将发动机舱内的小零件也包含在计算模型中(主要是管路和线束)，那么热管理仿真计算在车辆开发前期预测零件温度的准确度就会提高，进而可以采取有效措施保护耐热较差的区域，减少后期开发成本；另一方面，即使建立的数学模型并不是十分完善，也可以通过瞬态仿真的温升趋势，结合周围其他零件的布置情况，推断出零件受热情况，在项目开发前期规避潜在风险。

3.2 RadTherm瞬态计算在车辆开发前期的应用

本文中对某轿车发动机舱前围板隔音棉进行了瞬态仿真计算，隔音棉的作用在于减小从发动机舱传递到乘客舱的发动机振动噪声，如果表面温度过高将导致隔音棉老化，进而降低隔音效果，更严重的是导致隔音棉起火。

图6为隔音棉在没有隔热铝箔情况下的温度分布。从图6和图5可以看出，隔音棉中间深色区域的温度远远超过其温度限值，在发动机熄火后的4min内达到峰值，整个过程中超过温度限值的时间持续了9min，所以隔音棉过热区域需要加设隔热罩。图7为隔热罩的原始设计方案，该方案是根据工程经验设计出来的。经过试验验证，原始设计方案已经能使隔音棉满足热性能要求，但还没有达到最佳效果。图8的隔热罩根据瞬态计算结果得出改进方案，而图9为隔热罩改进后隔音棉的温度分布图。从图中可以看出，改进方案能满足设计要求，而且改进后的隔热罩面积只有原先的40%，选用改进方案可以节省成本60%。总之，单纯的稳态计算已经不能满足整车开发需求，将瞬态计算加入到整车开发过程是很有必要的。

4 结论

(1) 在车辆开发前期，利用虚拟技术对靠近排气系统附近的零件进行瞬态计算分析是可行和必要的，而且这种计算方法简便、快捷，可以在项目开发前期的整车热管理中得到广泛应用。

(2) 利用瞬态分析手段，对隔音棉隔热罩进行改进设计，通过比较改进前后的温度场分布，最终选用改进方案，使零件成本降低60%。

(3) 仿真结果与试验结果之间的误差在5%～10%之间，主要与数模网格建立的完善程度有关，直径10mm以上的管路应该体现在计算模型中，这样才能保证真实的对流换热和热辐射环境，为瞬态计算提供准确的边界条件，从而得到更为精确的计算结果。

[1] Alkidas A C, Battiston P A. Thermal Studies in the Exhaust System of a Diesel-Powered Light-Duty Vehicle[C]. SAE Paper 2004-01-0050.

[2] Tentner Adrian, Froehle Paul, Chunyi Wang. Modeling and Analysis of Transient Vehicle Underhood Thermo-Hydrodynamic Events Using Computational Fluid Dynamics and High Performance Computing[C]. SAE Paper 2004-01-1511.

[3] Yang Zhigang, Bozeman Jeffrey, Fred Z Shen. CFD for Flow Rate and Air Re-Circulationat Vehicle Idle Conditions[C]. SAE Paper 2004-01-0053.

[4] RadTherm Technical Manual v9[G].Thermo Analytics, Inc.,2009.

[5] Ernst Peter Weidmann, Thomas Binner, Heinrich Resiter Daimmler. Experimental and Numerical Investigations of Thermal Soak[C]. SAE Paper 2008-01-0396.

[6] Franchetta M, Bancroft T G. Fast Transient Simulation of VehicleUnderhood in Heat Soak[C]. SAE Paper 2006-01-1606.