脆性聚甲基丙烯酸甲酯板动态裂纹传播有限元模拟

张振亚，麻鸳鸳，周风华

(宁波大学冲击与安全工程教育部重点实验室，浙江宁波315211)

0 引言

20 世纪80 年代以来，脆性材料中动态裂纹传播问题得到广泛关注，取得了大量的实验数据和理论研究成果［1-6］。但脆性材料在裂纹传播过程中特有的物理现象，比如镜面-抛物线-周期凹槽-分叉现象，以及特有的耗能模式，从数学上或经典断裂力学上都还无法解释，因此实验手段和有限元分析是探索这些问题很好的手段。

对于动态裂纹传播的行为，尽管有很多种研究方法，但数值模拟计算方法不失是一种很有效、合理的估计方法。目前有很多种模拟动态传播过程，传统方法使用动态应力强度或者J 积分作为断裂准则。Nishioka 等把动态J 积分引入有限元网格成功模拟裂纹的传播和扭结现象［7-8］，此方法能够抓住裂纹尖端的奇异性，但要想获得裂纹尖端的较好网格需要重新划分网格技术。Belytschko 等［9］、Moes等［10］提出扩展的有限元法(XFEM)，这种方法的优点不需要重新划分网格就能模拟任意裂纹，但它的算法过多依赖设定路径的质量，对于比较复杂裂纹模式这个算法的精度难以保证。近年来，内聚力单元方法被广泛用于模拟裂纹传播行为，Camacho 等首先提出了一个简单的刚性不可逆的内聚力准则［11-12］，pandolfi 等［13-14］运用此准则成功进行3D分析一些工程问题。基于材料的本身性质后来还出现了各种内聚力模型，如率无关和率相关等，这些数值方法都是基于自己的程序，对于动态裂纹传播问题收敛较困难，需要调节参数。本文基于通用的大型软件ABAQUS 处理器，该软件算法比较成熟，容易收敛而且精度相对较高，结合开发的用户子程序，这样更加符合实际材料的物理背景。

本文是基于实验的基础上，基于内聚力单元方法，结合编制材料的用户材料子程序，嵌入有限元软件ABAQUS 求解器来模拟裂纹扩展行为。有限元模拟结果显示:能够抓住脆性材料聚甲基丙烯酸甲酯(PMMA)动态裂纹传播中特有的状态量(包括裂纹最小传播速度、裂纹传播速度、微分叉，局部分叉、裂纹传播极限速度)。

1 动态裂纹传播实验

1.1 实验条件

选用无色透明的PMMA 板材作为实验材料，材料厚度D=3 mm，质地均匀，结构较为致密。材料的弹性模量E=3 000 MPa，泊松比υ =0.35，密度ρ =1.2 g/cm3. 将PMMA 板材裁为5 种不同尺寸的矩形，夹持在特制夹具中［15］。夹持后的试件实验区域为长、宽分别是L×h 的5 种矩形，具体尺寸分别为:A 型(320 mm×240 mm)、B 型(320 mm ×200 mm)、C 型(320 mm ×160 mm)、D 型(240 mm ×240 mm)和E 型(240 mm ×200 mm). 利用丝网印刷技术在裂纹传播区域顺次布置等间距d =2.5 mm 的银漆导电线路，每根线宽度为0.6 mm，导电线的厚度为10 μm. 实验的其他方面在文献［16］有详细的描述。

1.2 实验结果

实验结果主要包括3 个部分:裂纹传播速度，裂纹传播速度与断裂能关系和裂纹断面留下的遗迹(局部分叉，宏观分叉)。

如图1 所示，裂纹速度经历一个短暂加速阶段进入传播速度稳定段，且裂纹传播速度最小值大约为215 m/s，这时的断裂能为950 J/m2;裂纹传播速度的最大值为650 m/s，对应的断裂能大约为14 000 J/m2.

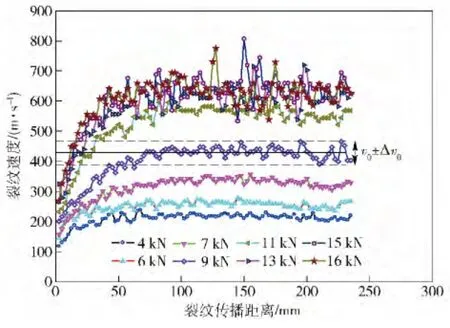
图1 E 型试件在不同载荷作用下的裂纹传播速度随传播距离的变化曲线Fig.1 Crack propagation velocities of E-type specimen under different loadings

如图2 所示，裂纹稳定传播速度v0是预加能量的单调递增函数，并且材料表现出速度增韧现象。

如图3 所示，这是裂纹传播后留下的遗迹，从图3(a)可以看出v0＜580 m/s，裂纹传播路径是一条直线，没有出现局部分叉现象;图3(b)描述了裂纹传播速度v0在580 ～600 m/s 这个范围，裂纹传播路径发生了弯曲，伴有对称局部分叉产生，局部分叉的特征随着裂纹传播速度的增加，局部分叉越来越多，但裂纹的厚度没有穿透试样的厚度。这个阶段从某种程度上反映了裂纹传播开始出现失稳;图3(c)代表了裂纹传播速度达到610 m/s，裂纹传播路径开始出现宏观一次分叉，随着裂纹速度的提高，会出现多次分叉和次级分叉现象。由于提前裂纹出现分叉，无论施加的能量多大，单一主裂纹速度都不会增加下去，此时裂纹传播速度的最大值为665 m/s，大约为材料的瑞丽波速cR的70%(PMMA材料的cR=930 m/s).

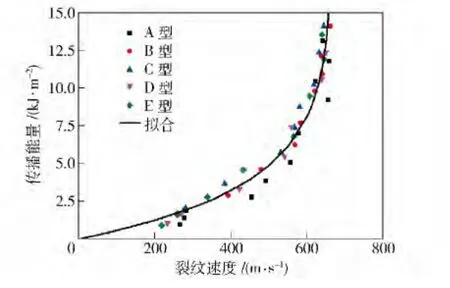
图2 裂纹的动态传播能与稳定传播速度之间的关系Fig.2 The relationship between the dynamic propagating energy and the crack propagation velocity

图3 裂纹传播的轨迹和分叉图(图片上导电线间隔包括线宽为2.5 mm)Fig.3 Straight paths，local bifurcations and macro bifurcations of the propagating crack (the interval of conductive lines，including line width，is 2.5 mm)

2 动态裂纹传播模拟

2.1 内聚力准则

混合型内聚力模型用于内聚力单元的本构关系，这种情况存在内聚力单元存在法向变形和剪切变形，即法向张开位移δn和剪切张开位移δs，有效张开位移δeff可以表示为

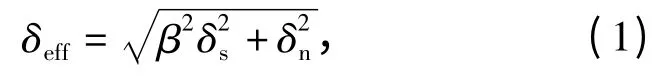
式中:β 表示法向张开位移和剪切张开位移占有的权重。有效拉应力σeff表示为

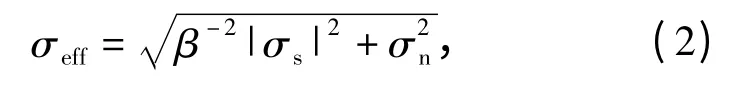
式中:σs表示剪切拉应力;σn为法向拉应力。内聚力准则是描述δeff与σeff之间的关系，普遍形式如下:

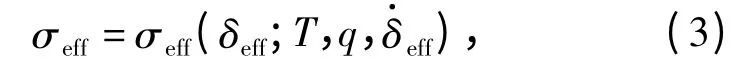
在本文有限元模拟中，利用一个简单不可逆的线性衰减内聚力模型，在该模型中，首先忽略率相关的影响。内聚力的模型的形状如图4 所示。

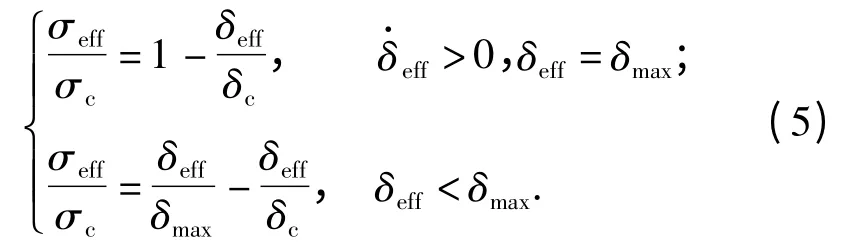
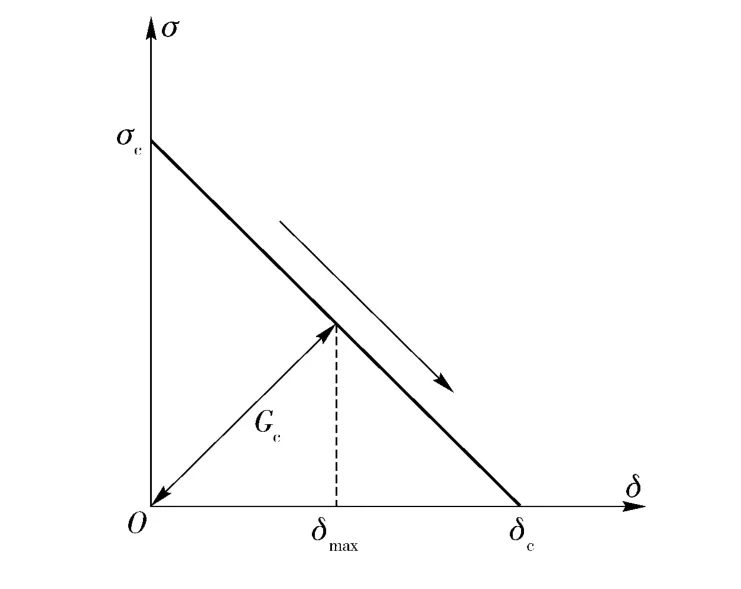
图4 初始刚度线性衰减不可逆内聚力准则Fig.4 The initial-rigid linear-decay irreversible cohesive law

假设脆性材料PMMA 的临界应力σc是定值，而临界张开位移δc随着张开速度增加，这样的率相关内聚力准则联系着裂纹尖端断裂过程，最终将导致伴随微裂纹过程消耗更多的能量，这样的内聚力模型能够准确地描述脆性材料的断裂过程。因此用下面的式子来描述δc和的关系

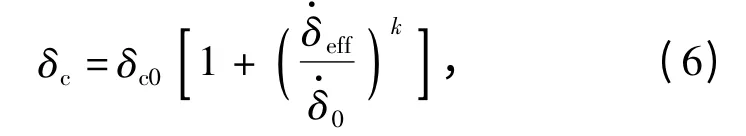
式中:δc0、和k 都是材料参数;δc0是静态的裂纹张开位移是裂纹张开位移变化率;k 是率相关系数。率相关的内聚力模型如图5 所示。

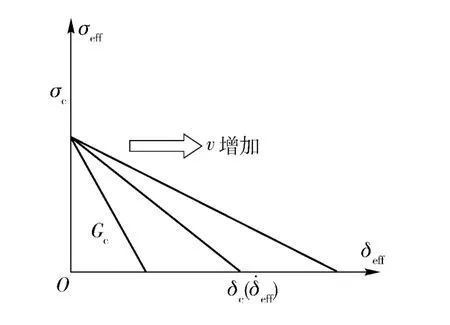
图5 率相关的内聚力准则Fig.5 The rate-dependent cohesive law

σc是最大的内聚力，δc是临界张开位移。图4和图5 中曲线所围的面积就是裂纹面单位面积消耗的能量，即断裂能Gc.

式中:Γc表示产生裂纹面的表面能。

2.2 材料参数

选用的材料是有机玻璃PMMA，材料性质:密度ρ=1 200 kg/m3，杨氏模量E =3 000 MPa，泊松比ν=0.35. 对于率无关的内聚力模型，最大内聚力σc和临界张开位移δc是定值，在室温状态下材料PMMA表现出较小的塑性。而材料PMMA 的最大抗拉强度范围是75 ～76 MPa，计算时选择75 MPa. 实验时发现材料PMMA 断裂能Gc在420 ～480 N/m，因此选择断裂能Gc=450 N/m. 临界张开位移δc根据(7)式计算出为12 μm. Gc也就是材料PMMA 静态断裂韧性。静态裂纹前端内聚区的大小可以用Rice［17］公式估算如下:

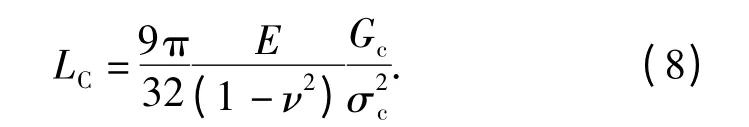
利用(8)式可以计算出内聚力区的大小为0.24 mm.

2.3 有限元模型

计算模型是三维有限元模型。因为实验中的几何尺寸太大，选择缩小的板来模拟。板的几何尺寸:L =32 mm(x 轴)，高h =16 mm(y 轴)，厚度t =0.5 mm(z 轴)。有限元模型中所用的单元为:内聚力单元COH2D4，一般单元CPE3(三节点线性平面应变单元)，网格排列如图6(a)所示，节点总数为51 884，单元总数为43 027. 板沿着垂直中心线有4 mm边缘裂纹，板在y 轴施加一个相等边界位移载荷Δ+和Δ-，试样上的x 轴方向是自由的。在这种载荷下，裂纹通常是沿着径向方向直线传播。储存在预加载荷板的单位面积的应变能W0计算如下:

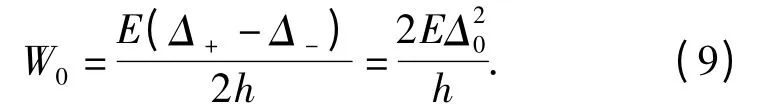
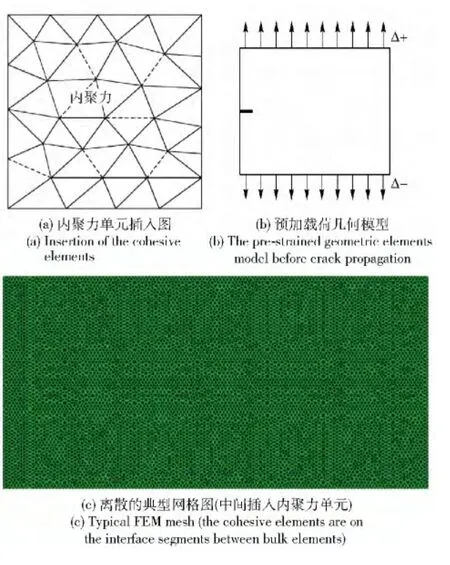
图6 网格形成与有限元模型Fig.6 FEM model and mesh

为了模拟实验的实际工况，模拟工作分为两个步骤:1)运行Plate_Preload.inp 文件，目的是计算出准静态预加载荷Δ+和Δ-下算出板内应力应变(即板内储存应变能);2)复制上步计算的结果文件Plate_Preload.Odb 和Plate_Preload. Prt 到当前文件夹，与Plate.inp 和裂纹起裂准则用户子程序Vumat一块运行。这样做的好处是一方面边界条件保持不变，同时把第1 步预加载荷算出的结果作为当前步已知条件(板内已经储存了应变能)，启动Vumat 即开动裂纹起裂准则，裂纹沿着设定的路径就会依次释放应变能。为了保证计算的精度和稳定性，模拟计算中设定时间步长为0.005 μs.

3 计算结果

3.1 率无关模拟结果

要模拟裂纹在不同载荷下的传播速度情况，确定预加边界位移δ0分别为0.045 mm、0.050 mm、0.055 mm、0.060 mm、0.065 mm、0.070 mm、0.080 mm，储存在板内的能量分别为759 N/m、965 N/m、1 134 N/m、1 360 N/m、1 584 N/m、1 837 N/m、2 400 N/m. 裂纹传播速度v0确定:在计算后处理中定义固定输出的时间Δt，裂纹传播的距离近似等于相邻裂纹尖端输出坐标差值Δl(裂纹直线传播是精确满足，传播路径发生弯曲近似满足)，因此裂纹传播速度为v0= Δl/Δt. 依此方法计算结果如图7 所示。从图7 可以看出:1)对于每一次实验，动态裂纹传播都是经历了一个短暂的加速阶段，裂纹传播速度达到一个稳定速度v0，而且裂纹传播路径几乎是直线传播一直到断裂;2)裂纹稳定传播速度的最小值大约为235 m/s，正如图中蓝色虚线所示，也就是裂纹传播速度小于这个值裂纹就会止裂不向前传播，最大裂纹传播速度为665 m/s，图上黑色虚线表示的，无论外载荷再高，裂纹传播都不会超过这个速度，并且裂纹传播在低速时，即v0≤500 m/s，裂纹传播速度变化较小，高速传播时裂纹传播速度变化较剧烈。只有当高载荷的情况下，即板内储存较高的能量下，裂纹传播速度达到580 m/s 左右，正如图8(b)所示裂纹的传播路径会发生一点弯曲，并且沿着裂纹传播路径两边对称出现微分叉。这些裂纹传播速度以及裂纹传播特有现象(微分叉、分叉)与实验结果相契合，差别之处实验中出现这些结果较模拟需要更高的能量，正如图11 所示，在相同载荷下，率无关模拟结果远远大于实验结果，出现的原因:裂纹传播速度较大，模拟选择Gc=450 N/m，对于PMMA这个材料太小，不能很好地反映材料的惯性效应。

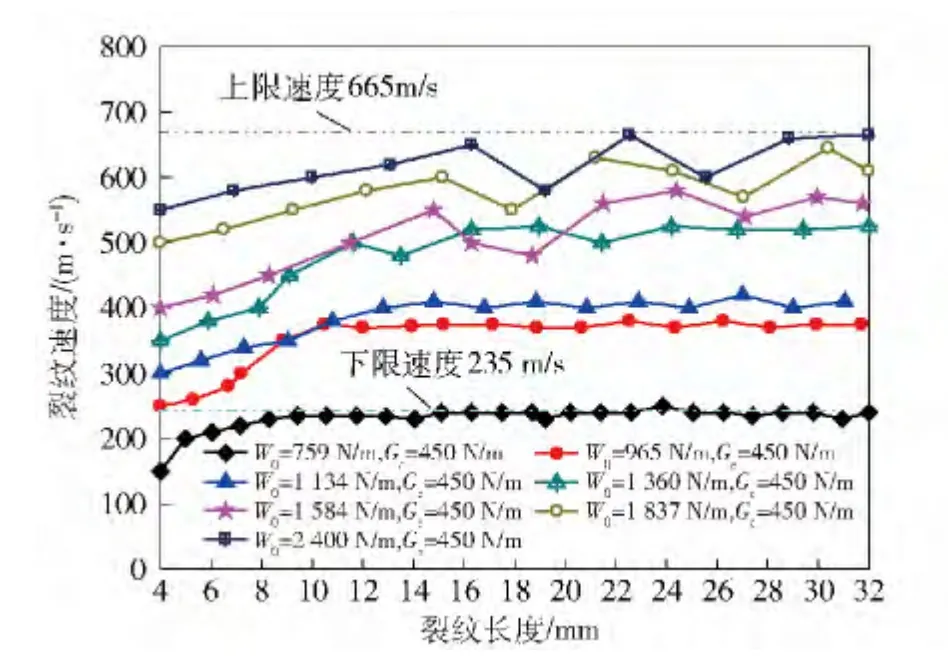
图7 裂纹速度随试样长度的变化曲线(利用率无关内聚力准则)Fig.7 Crack propagation velocity vs. specimen length. Simulations using rate-independent cohesive law

图8 时间t=40 μs 时在不同载荷下的裂纹扩展云图Fig.8 Crack propagation paths under different pre-loadings at 40 μs

3.2 率相关模拟结果

在这个率相关内聚力模拟计算中有4 个参数σc、δc0、k 需要确定。与前面计算相似，指定临界应力σc=75 MPa，静态临界张开位移δc0=0.012 mm.可见静态断裂能Gc=450 N/m. 为了避免复杂的参数调试，假设k=1. 裂纹张开变化率决定率相关的程度，一个非常小的就会体现很明显的率相关性。在计算中选定10 m/s，图9 给定了t=30 μs 时刻时相同载荷、不同应变率的裂纹扩展云图。从图9 可以看出，值越大，裂纹传播距离就越远，意味着裂纹传播速度就越大。

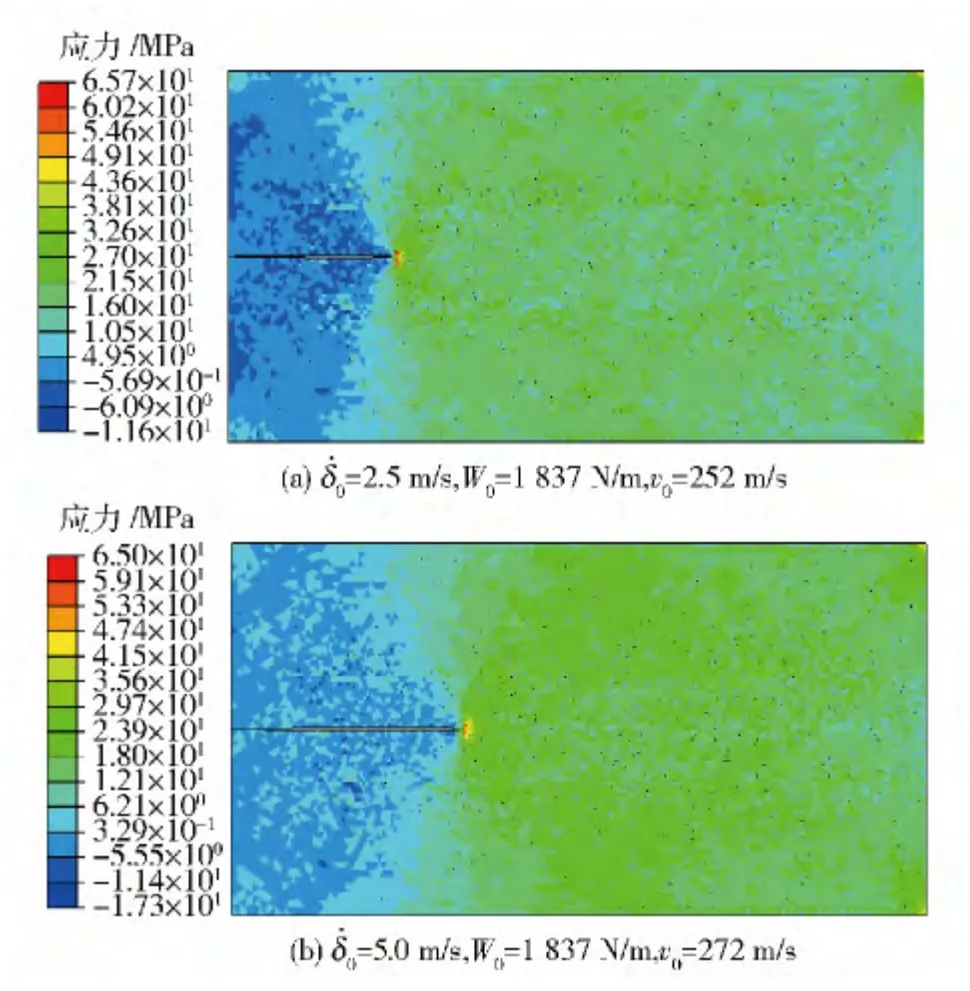
图9 时间t=30 μs 时在相同载荷下的裂纹扩展云图Fig.9 Crack propagation paths under W0 =1 837 N/m preloading at 30 μs. The rate-dependent cohesive law is used

图10 不同载荷下裂纹传播速度随裂纹长度的变化曲线=5 m/s)Fig.10 The crack propagation velocity vs. specimen length.Simulations using rate-dependent cohesive law =5 m/s)

3.3 裂纹分叉

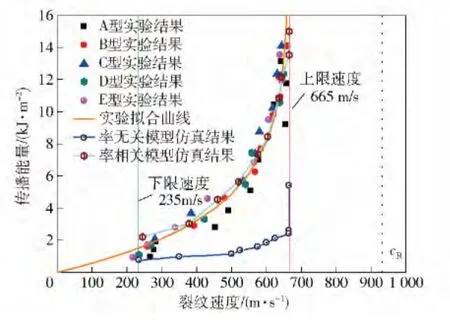
图11 实验结果与模拟结果对比图Fig.11 The comparison of the experimental results and simulation results

采用率相关的内聚力模型来模拟裂纹分叉，在该模拟计算中，内聚力参数如前面一样:σc=75 MPa，δc0=0.012 mm，k =15 m/s. 计算结果如图12. 从计算结果可以看出，在W0≈7 350 N/m，裂纹传播速度大约为v0=580 m/s 时，裂纹开始出现对称的微分叉，微分叉几乎贯穿了试样的厚度，随着裂纹速度进一步加大，正如图12(b)，裂纹传播路径发生弯曲，有的微分叉开始发展成为一次分叉，有的保持微分叉，微分叉的数量明显减少，可见微分叉发展为一次分叉消耗了大量的能量，与图3(b)的结果基本是一致的。裂纹传播速度继续加大，即W0≈12 180 N/m，v0≈645 m/s 时，裂纹传播路径发生弯曲，接着出现一次分叉、二次分叉，速度达到660 m/s，裂纹还出现次级分叉，由于分叉过早的出现，消耗了一部分能量，导致了材料PMMA 的上极限速度永远达不到瑞利波速cR.

4 结论

利用Cohesive 单元法，开发用户材料子程序，结合ABAQUS 求解器模拟脆性材料PMMA 动态裂纹传播行为。模拟计算过程中考虑采用率无关和率相关两种情况，其模拟结果如下:

1)相同载荷下，采用率无关内聚力准则模拟的稳定裂纹传播远大于实验测出的稳定裂纹传播速度。

2)无论是采用率无关还是率相关的内聚力准则，模拟出的裂纹传播速度的上限速度都是665 m/s，下限速度为235 m/s，与实验测试结果是吻合的，这也说明了这是材料PMMA 固有的材料属性，与其他无关。

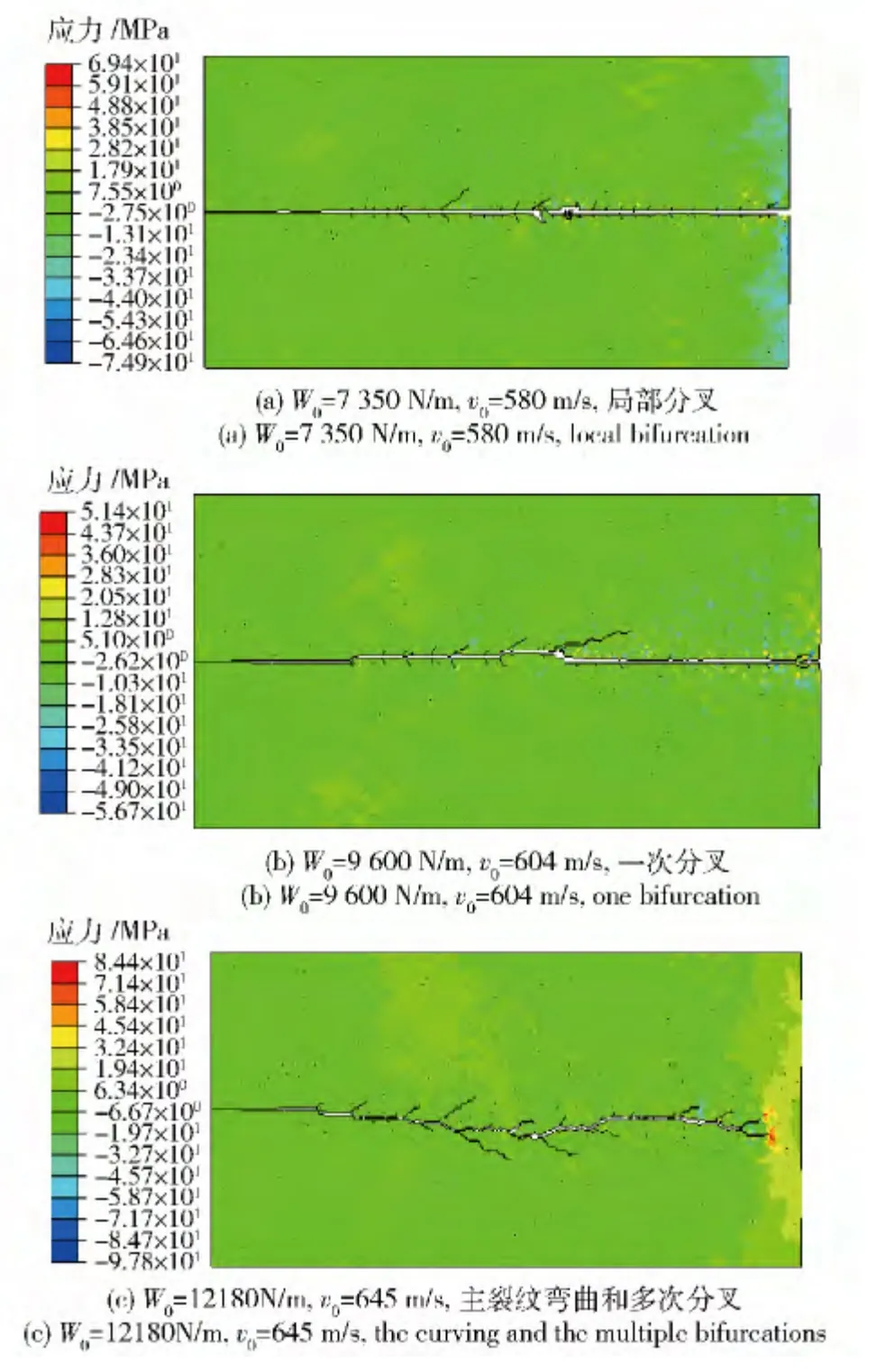
图12 =5 m/s 时在不同载荷下裂纹分叉图Fig.12 The bifurcations of cracks under different loads

3)利用率相关的内聚力模型能够较好地模拟裂纹传播行为，模拟结果与实验结果基本一致(见图11)，说明对于脆性材料PMMA，必须要考虑裂纹尖端张开位移变化率，这样能够消耗很多的能量。

References)

［1］Ravi-Chandar K，Knauss W G. An experimental investigation into dynamic fracture—Ⅳ. On the interaction of stress waves with propagation cracks［J］. International Journal of Fracture，1984，26(3):189 -200.

［2］Fineberg J，Marder M. Instability in dynamic fracture［J］. Physical Reports，1999，313:1 -108.

［3］Scheibert J，Guerra C，Dalmas D. Brittle-quasibrittle transition in dynamic fracture:an energetic signature［J］. Physical Review Letters，2010，104:045501.

［4］Xia K W，Chalivendra V B，Rosakis A J. Observing ideal“selfsimilar”crack growth in experiments［J］. Engineering Fracture Mechanics，2006，73:2748 -2755.

［5］Fineberg J，Gross S P，Marder M. Instability in dynamic fracture［J］. Physical Review Letters，1991，67:457 -460.

［6］Fineberg J，Gross S P，Marder M. Instability in the propagation of fast cracks［J］. Physical Review B，1992，45:5146 -5154.

［7］Nishioka T. Recent developments in computational dynamic fracture mechanics［C］∥Aliabadi M H. Dynamic Fracture Mechanics Int Series Comput Engng. Southampton，UK，and Boston，US:Computational Mechanics Publications，1995:1 -60.

［8］Nishioka T，Tokudome H，Kinoshita M. Dynamic fracture-path prediction in impact fracture phenomena using moving finite element method based on Delaunay automatic mesh generation［J］.International Journal of Solids and Structures，2001，38 (5):273 -301.

［9］Belytschko T，Black T. Elastic crack growth in finite elements with minimal remeshing［J］. International Journal for Numerical Methods in Engineering，1999，45(6):1 -20.

［10］Moes N，Dolbow J，Belytschko T. A finite element method for crack growth without remeshing［J］. International Journal for Numerical Methods in Engineering，2000，46(1):31 -50.

［11］Camacho G T，Ortiz M. Computational modelling of impact damage in brittle materials［J］. International Journal of Solids and Structures，1996，33(2):899 -938.

［12］Camacho G T，Ortiz M. Adaptive Lagrangian modelling of ballistic penetration of metallic targets［J］. Computer Methods in Applied Mechanics and Engineering，1997，142:269 -301.

［13］Pandolfi A，Krysl P，Ortiz M. Finite element simulation of ring expansion and fragmentation:the capturing of length and time scales through cohesive models of fracture［J］. International Journal of Fracture，1999，95:279 -297.

［14］Pandolfi A，Guduru P R，Ortiz M，et al. Three dimensional cohesive-elements of dynamic fracture in C300 steel［J］. International Journal of Solids and Structures，2000，37:3733 -3760.

［15］张振亚，周风华. 脆性PMMA 带板中的动态裂纹传播实验［J］.实验力学，2012，27(4):401 -407.ZHANG Zhen-ya，ZHOU Feng-hua. Experiment of dynamic crack propagation in brittle PMMA strip［J］. Journal of Experimental Mechanics，2012，27(4):401 -407.(in Chinese)

［16］张振亚，段忠，周风华. 脆性裂纹动态传播过程中的速度振荡现象和理论分析［J］. 力学学报，2013，45(5):729 -738.ZHANG Zhen-ya，DUAN Zhong，ZHOU Feng-hua. Experimental and theoretical investigations on the velocity oscillations of dynamic crack propagating in brittle material［J］. China Journal of Theoretical and Applied mechanics，2013，45(5):729 -738.(in Chinese)

［17］Rice J R. The mechanics of earthquake rupture［C］∥Dziewonski A M，Boschi E. Proceedings of International School of Physics Enrico Fermi. North Holland:Physics of the Earth’s Interior，1980:555 -649.