解决不同类型指派问题的EXCEL模型

刘静, 刘昌海

(1. 九江学院图书馆, 江西 九江 332005; 2. 九江学院商学院, 江西 九江 332005)

解决不同类型指派问题的EXCEL模型

刘静1, 刘昌海2

(1. 九江学院图书馆, 江西 九江 332005; 2. 九江学院商学院, 江西 九江 332005)

指派问题, 运筹学分支整数规划的一种应用, 主要用于解决资源配置方面的问题. 通过EXCEL建立了不同类型指派问题的模型, 旨在得到最优化的方案, 并可将该模型应用于组织的管理活动, 提高经济效益.

指派问题; EXCEL; 整数规划; 标准指派; 模糊指派; 广义指派

引言

组织的管理者经常要制定一些有关于资源配置的决策, 以便更好地实现组织目标. 许多情况下, 不同的资源需要在同一时间内、不同的经营活动、经营部门或个人之间进行分配, 然而资源是有限的. 为了使有限的资源能够最大限度地发挥作用, 需要将资源与需求者进行优化配置, 这就要应用到线性规划中的整数规划.

1 指派问题简介

指派问题是运筹学数学规划中整数规划的一种应用.

运筹学是应用分析、试验、量化的方法, 对经济管理系统中人力、物力、财力等资源进行统筹安排, 为决策者提供有依据的最优方案, 以实现最有效的管理[1].

整数规划是从1958年由R.E.戈莫里提出割平面法之后形成独立分支的[2], 整数规划是指部分或全部变量限定取整数值的一种线性规划[3]. 整数规划问题在经济与管理中的应用比较广泛, 如可应用在指派、产品设计、市场份额、投资场所的选择和固定成本分布系统设计等方面.

指派问题 (Assignment Problem), 也称分配或配置问题, 是资源合理配置或最优匹配问题[4]. 如把M个任务分配个N个人, 由于每个人的能力与特点不同, 完成每项任务的所产生的效益或需要的时间也不相同, 指派问题所要解决的就是在人与任务之间如何指派, 才能使总体效益最大或总用时最少[5]. 指派问题属于整数规划中的纯整数规划,

2 指派问题的类型

根据人数与任务数的关系, 指派问题可以分为二类:

1)标准型（平衡型）指派问题. 即人数M与任务数N相等, 每个人只能分配一项任务[6].

2)非标准型指派（又称广义指派、模糊型指派、竞争型指派、非平衡性指派）问题, 即人数M与任务数N不等, 这又可以分为以下二种情况:

①M>N, 即任务数M多于人数N, 这时, 需要一人兼多项任务才能完成全部任务的分配;

《纲要》中指出：幼儿园教育应为幼儿提供自由活动的机会，支持幼儿自主地选择计划活动，为每个幼儿提供表现自己长处和获得成功的机会，增强其自信心。经常性的为幼儿提供作品展示平台，源源不断的激发幼儿创作兴趣。

②M

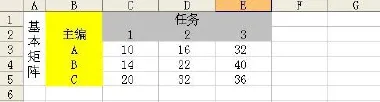
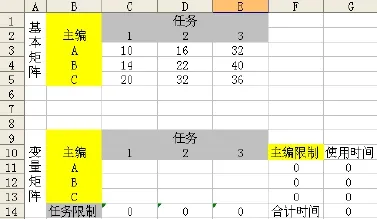
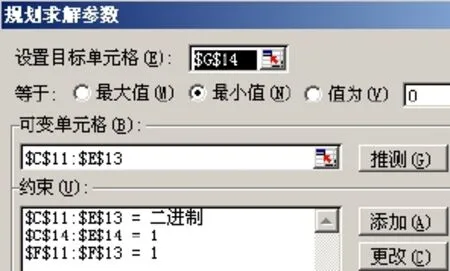
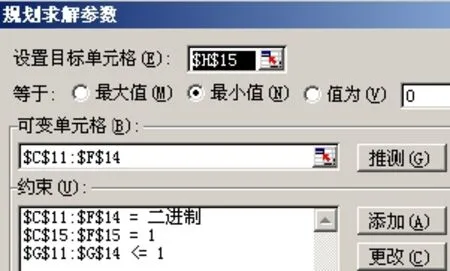
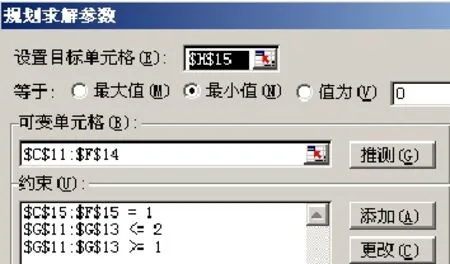
3 利用EXCLE进行指派问题的建模

EXCEL作为一种办公软件, 具有强大的计算功能, 完全可以EXCEL建模来实现不同类型的指派问题.

3.1 标准型（平衡型）指派问题（M＝N）

如某杂志社同时有3项任务需要分配给3位主编, 且每人必须分配一项任务. 由于这3位主编的背景及能力不同, 因此完成任务所需的时间也不相同, 如表1所示, 请问如何进行任务分配使完成全部任务所用时间最少？

表1 标准型（平衡型）指派问题Form 1 The standard type (balance) assignment problem

用EXCEL建模, 步骤如下:

3.1.1 设计基本矩阵

图1基本矩阵Figure 1 Basic matrix

3.1.2 设计变量矩阵

图2 基本矩阵与变量矩阵的设置Figure 2 Basic matrix and matrix of variables set

1)设置C11: E13九个单元格中数字格式为“0”（单元格格式/数字/自定义/0）;

2)设置C14单元格值为C11、C12与C13三个单元格之和, 即在C14单元格输入“=SUM（C11: C13）”（输入时不包括引号, 下同）. 同理设置D14与E14单元格分别为D11: D13、E11: E13之和, 可分别单独设置, 亦可使用格式拖动方式, 即选中C14单元格, 鼠标指向左下角, 会出现个十字形的图标, 然后向右拖动二格;

3)设置F11单元格值为C11、D11与E11三个单元格之和, 同理设置F12与F13单元格分别为C12: E12、C13: E13单元格之和;

4)应用函数设置G11单元格, SUMPRODUCT函数不但可以计算数据区域中满足条件的数据累加和, 还可以计算数组乘积的累加和[7], 即在G11单元格内输入“=SUMPRODUCT(C3: E3, C11: E11)”, 即该二行对应的单元格值先相乘再加总; 设置G11单元格: 设置单元格格式/“数字”标签/分类: 数值-小数位数: 0. 同理, 分别设置G12及G13;

5)设置G14单元格值为G11: G13三个单元格值之和.

3.1.3 利用EXCEL工具栏中的“工具/规划求解”进行以下设置, 最后点击“求解”[8]

1)设置规划求解参数（工具/规划求解/选项/）, 在“假定非负”前打勾;

2)设置目标单元格, 即G14单元格;

3)设置可变单元格: 即C11: E13区域共九个单元格;

4)添加约束条件, 如图3:

①设置C11: E13九个单元格中的数值为二进制（约束-添加-单元格引用位置: $C$11:$E$13-逻辑关系: bin-约束值: 二进制）, 即只能取值0或1, 即如某位主编被分配到某项任务, 则对应的单元格值为1, 否则为0;

②设置C14: E14三个单元格中的数值＝1,即每项任务都应当被分配出去, 且只能被分配一次;

③设置F11: F13三个单元格中的数值＝1,即每人都应当被分配到任务, 且只能被分配一项任务.

图3 M=N时约束条件的设置Figure 3 When M=N set constraints

5)点击“求解/保存规划求解结果”, 如图, 即分别将任务1分配给B, 任务2分配A, 任务3分配给C, 完成全部任务需要的最少时间为66, 如图4.

图4 M＝N时指派任务分配结果Figure 4 When M =N assigned task allocation results

3.2 非标准型指派（广义指派、模糊型指派、竞争型指派）问题（M

非标准型指派问题必须转化为标准型指派问题[6]. 假设任务数不变, 人数增加1人, 即同时有3项任务需要分配给4位主编, 且每人最多只能分配其中1项任务.此时, 可通过增加虚拟任务数的方法使人数与任务数相等[9],然后再应用M＝N时所采用的方法与步骤.

因第4个任务为虚拟任务, 因此F3: F6单元格值应为0; 由于4位主编只需要承担3项任务, 且每人至多只能承担1项, 这就意味着将有一位主编无法被分配到任务, 因此每个主编承担的任务数为1或0. 更改相关约束条件, 点击求解, 得到的结果是: C没有被分配到任务, 完成全部任务需要的最少时间为60, 如图5、图6.

图5 M

图6 M

3.3 非标准型指派（广义指派、模糊型指派、竞争型指派）问题（M>N）

假设人数不变, 增加一项任务, 即同时有4项任务需要分配给3位主编, 每位主编至少应承担一项, 且最多不超过二项任务. 此时, 因人数与任务数不对称, 因此通过增加虚拟人数的方法使人数与任务数相等; 然后再应用M=N时所采用的方法与步骤, 只需更改相关约束条件即可, 如图7:

图7 M>N时约束条件的设置Figure 7 When M>N set constraints

因D为虚拟人, 因此C6: F6单元格值应为0; 由于3位主编需要承担4项任务, 且每人至少应承担一项, 最多只能承担两项任务, 因此每个主编承担的任务数为1或2. 更改相关约束条件, 点击求解, 得到的结果是: A需同时承担任务2及任务4,完成全部任务需要的最少时间为87. 如图8.

图8 M>N时指派任务分配结果Figure 8 When M >N assigned task allocation results

4 结论

综上所述, 本文根据实例, 通过利用EXCEL对指派问题进行建模, 使用者只需在基本矩阵中输入相应数值即可轻松完成求解, 简化了计算步骤, 缩短了决策时间, 提高了工作效率, 并使利用现代计算机技术解决优化类问题更具有普遍性与现实意义.

[1] 韩伯棠. 管理运筹学[M]. 高等教育出版社, 2005: 1.

[2] 达林. 切平面在混合整数非线性规划中的应用[D]. 北京: 北京交通大学, 2009:11.

[3] 贺德化. 管理决策中常见数学模型[M]. 兰州: 兰州大学出版社, 1988: 291.

[4] 熊伟. 运筹学[M]. 北京: 机械工业出版社, 2009: 123.

[5] 郑鸿钧. 指派问题的EXCEL求解模板[J]. 办公自动化, 2012(16): 20-27.

[6] 杜金玲, 周杰. 关于几种不平衡指派问题的修正匈牙利解法[J]. 价值工程, 2010(13): 120-123.

[7] 宁桂霞, 刘光凤. 浅谈Excel函数在高校教务管理中的应用[J]. 福建电脑, 2013(09): 160-165.

[8] 王贵强. 运筹学上机指南与案例导航[M]. 兰州: 兰州大学出版社, 2009: 47.

[9] 陈海伟, 王洁. 一类非平衡指派问题的求解[J]. 河南教育学院学报: 自然科学版, 2011(03): 16-21.

EXCEL model for solving different types of assignment problem

LIU Jing1, LIU Chang-hai2

(1. Jiujiang University Library, Jiujiang 332005, P.R.C.; 2. Business School, Jiujiang University, Jiujiang 332005, P.R.C.)

Assignment problem is an application of operations research branch of integer programming, mainly used to solve the problem of resource allocation. This paper establishes the different types of assignment problem model by EXCEL, aims to get the optimal solution, and applies the model to the organization's management activities to enhance economic efficiency.

assignment problem; EXCEL; integer programming; standard assignment; fuzzy assignment; generalized assignment

TP317.3

: A

: 1003-4271(2014)03-0456-05

10.3969/j.issn.1003-4271.2014.03.24

2014-03-06

刘静(1978-), 女, 汉族, 内蒙古人, 讲师.