基于小波多分辨技术重力场相关系数成像

刘志新，卢 海，2

（1：中国矿业大学 资源与地球科学学院，江苏 徐州221116；2：淮安市水利勘测设计研究院有限公司，江苏 淮安223001）

重力勘探是利用组成地壳的各种地层、岩体、矿体的密度差异所引起的重力变化而进行地质勘探的一种方法［1］.常规重力测量只观测到重力异常，在重力数据后期处理时往往将重力异常值转化成重力梯度异常和延拓重力异常［2-4］.常规重力异常反演方法是基于反演理论，使目标函数达到极小的线性或非线性反演［5］，存在多解性.Patclla等在1997年首次提出将概率成像法用于自然电位异常的解释［6］.Abdelrahman等［7］提出了相邻最小二乘重力异常的归一化互相关公式［7］.郭良辉等［8］提出了重力异常三维相关成像方法和重力梯度数据三维相关成像方法，并提出了基于异常分离的三维相关成像方法来提高成像分辨率，通过合成Y型岩脉模型和合成多个直立长方体组合模型的重力异常和重力梯度数据试验分析，验证了三维相关成像方法可显示出异常地质体的空间赋存状态和等效剩余质量分布，具有良好的纵向和横向分辨率［8-10］.徐令周等［11］利用概率成像方法对自然电场和大地电磁数据进行了研究，取得了一些进展和认识［12］.杨文采等［13］利用小波多分辨原理，在对中国布格重力异常多尺度分解的基础上，反演了各种尺度意义下中国大陆地壳的密度差异，给出了中国大陆地壳中相对密度差异的空间分布，利用离散小波变换进行重力异常多重分解为研究中国大陆地壳构造，进行深部地质研究提供了新成果和新方法.

本文提出的重力场参数相关系数成像方法能准确确定异常体的空间位置和延伸情况，首先给出重力/重力梯度异常相关系数的计算方法，结合设置的模型，得出基于小波多分辨技术的重力参数相关系数成像方法具有很高的横向、纵向分辨率，且相对于传统重力资料成像效果更加直观和清晰.

1 方法原理

重力异常值是指地下密度异常体在空间中产生的引力的垂直分量，设地下任意坐标为（xq，yq，zq）、体积为Vq的q点的剩余密度为Δσq，则它在空间上任意点（x，y，z）处产生的重力异常Δgq（x，y，z）可表示为

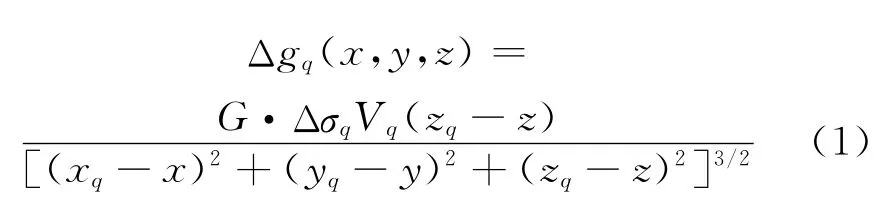
式中，G 为万有引力常数，G=6.666 7×10-11m3·kg-1·s-2

利用Abdelrahman等［7］提出的重力异常的相关公式，定义测区重力异常与q点剩余质量产生的重力异常两者的相关公式为

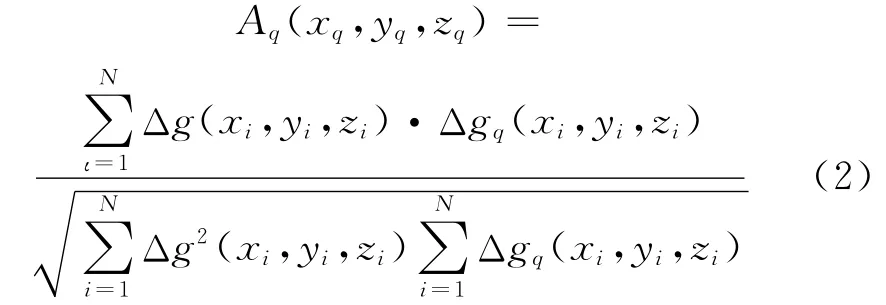
式中：Δg（xi，yi，zi）为测区第i个观测点的实测重力异常；（xi，yi，zi）为该测点的坐标；Δgq（xi，yi，zi）为测区下的q点剩余质量在该观测点的重力异常；N为总观测点数.

重力异常相关系数Aq的物理意义就是用地下q点在地表产生的重力异常值与实测重力异常值进行互相关计算，表示地表重力异常由地下q点产生的可能性的大小，如果Aq为正，则该点质量盈余，若为负，则该点质量亏损.

重力梯度异常的相关系数为

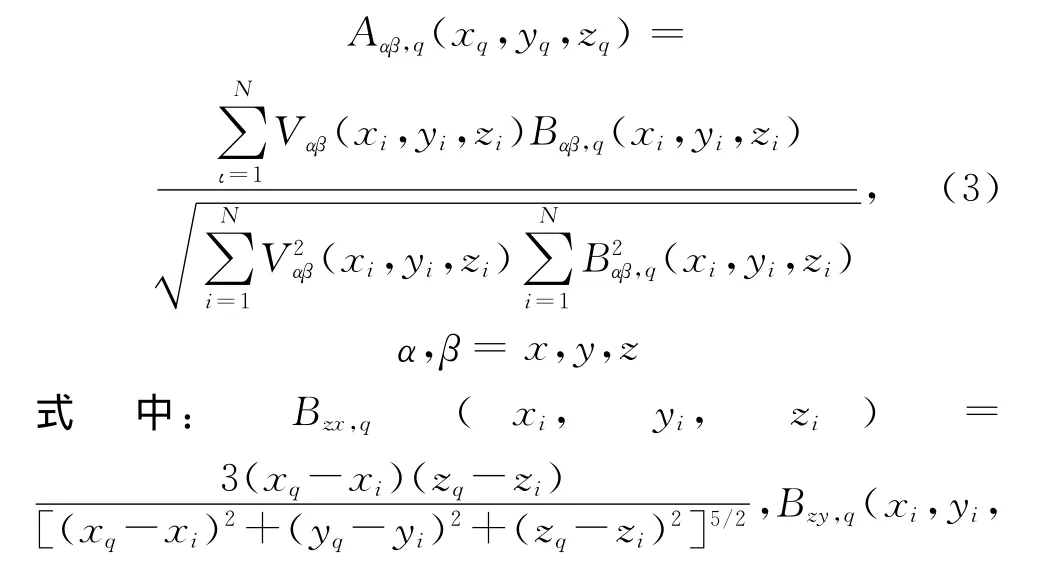
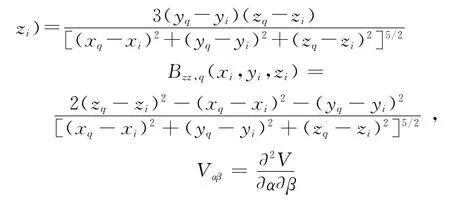
2 模型设置及其重力场参数

计算模型三维空间范围为0≤x≤20km、0≤y≤20km、-4km≤z≤0.由浅至深，由小到大共设置了10个异常体，分别为深层较大的A1、A2、A3，中层中等范围的B1、B2、B3、B4，浅层较小的C1、C2、C3.模型中各异常体的具体空间位置及密度参数见表1.

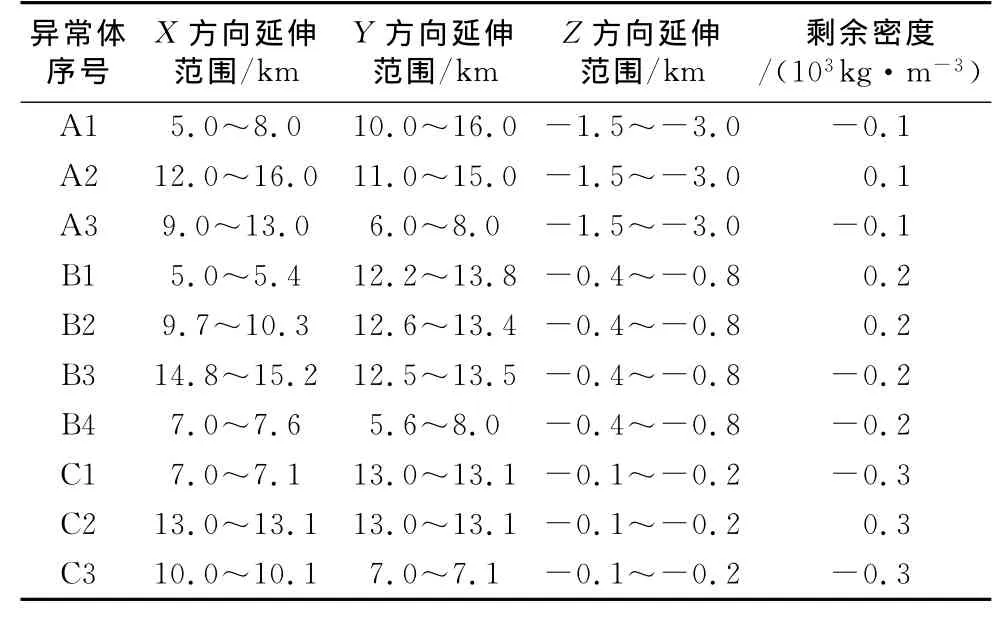
表1 模型几何参数和剩余密度Tab.1 Model geometry parameters and density

图1为异常体在地面上的投影，图2为Y=13.0km的断面切片图，该断面上包括C1、C2、B1、B2、B3、A1、A2这7个异常体.

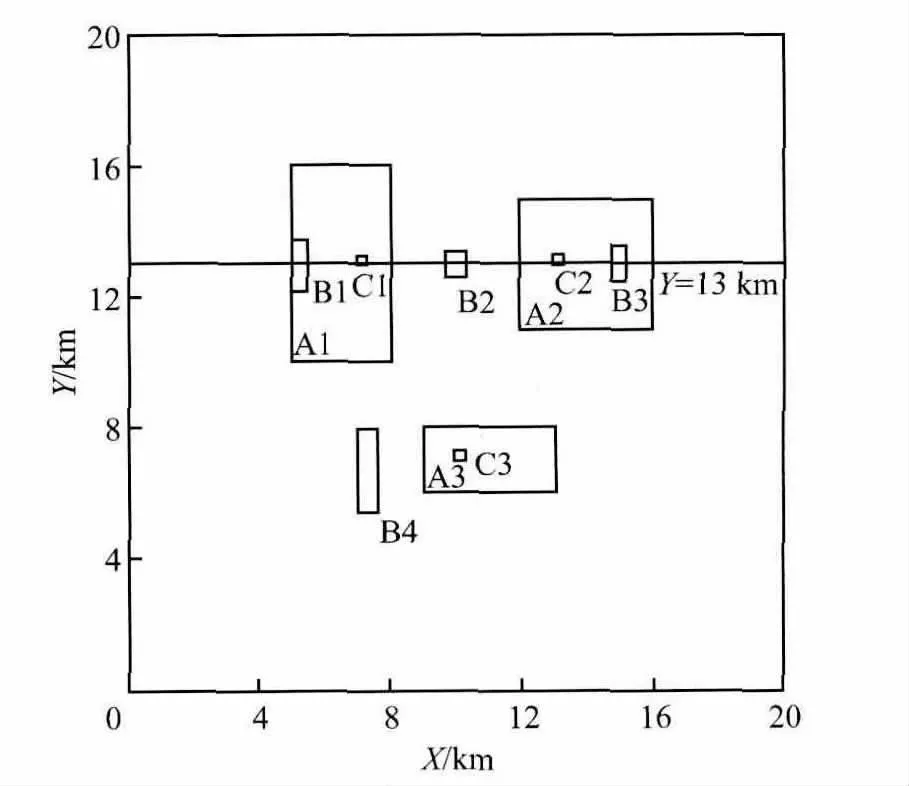
图1 模型平面投影Fig.1 Model plane projection map

计算地质体所产生的重力异常，通常是依据牛顿万有引力定律，首先计算地质体产生的引力位，重力异常是引力位沿重力方向上的导数，而重力梯度异常是重力异常在空间3个方向上的导数.如果代入计算的是地质异常体的剩余密度，那么得到的就是重力异常（单位：10-5m·s-2）和重力梯度异常值（单位：10-9s-2）.

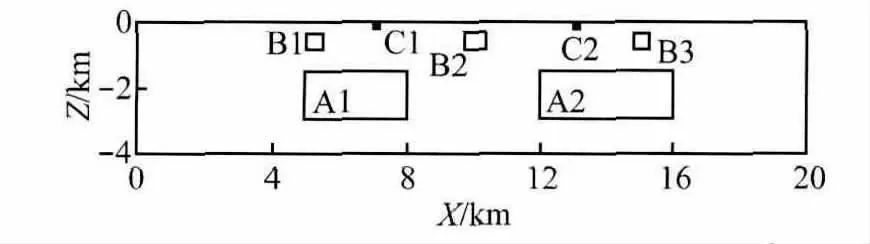
图2 模型Y＝13.0km断面切片Fig.2 Model Y＝13.0km section slice

图3a是剩余重力异常图，可以清楚地反映出A1、A2、A3、B1、B2、B3、B4几个较大异常体，C1、C2、C3反映不是很清晰；图3b是重力梯度异常Vzy，对各个级别的异常反应良好，通过该图可以区分出各个异常体引起的异常.可知，重力梯度异常相比于重力异常更能明显地突出异常特征，其结果具有更高的分辨率.

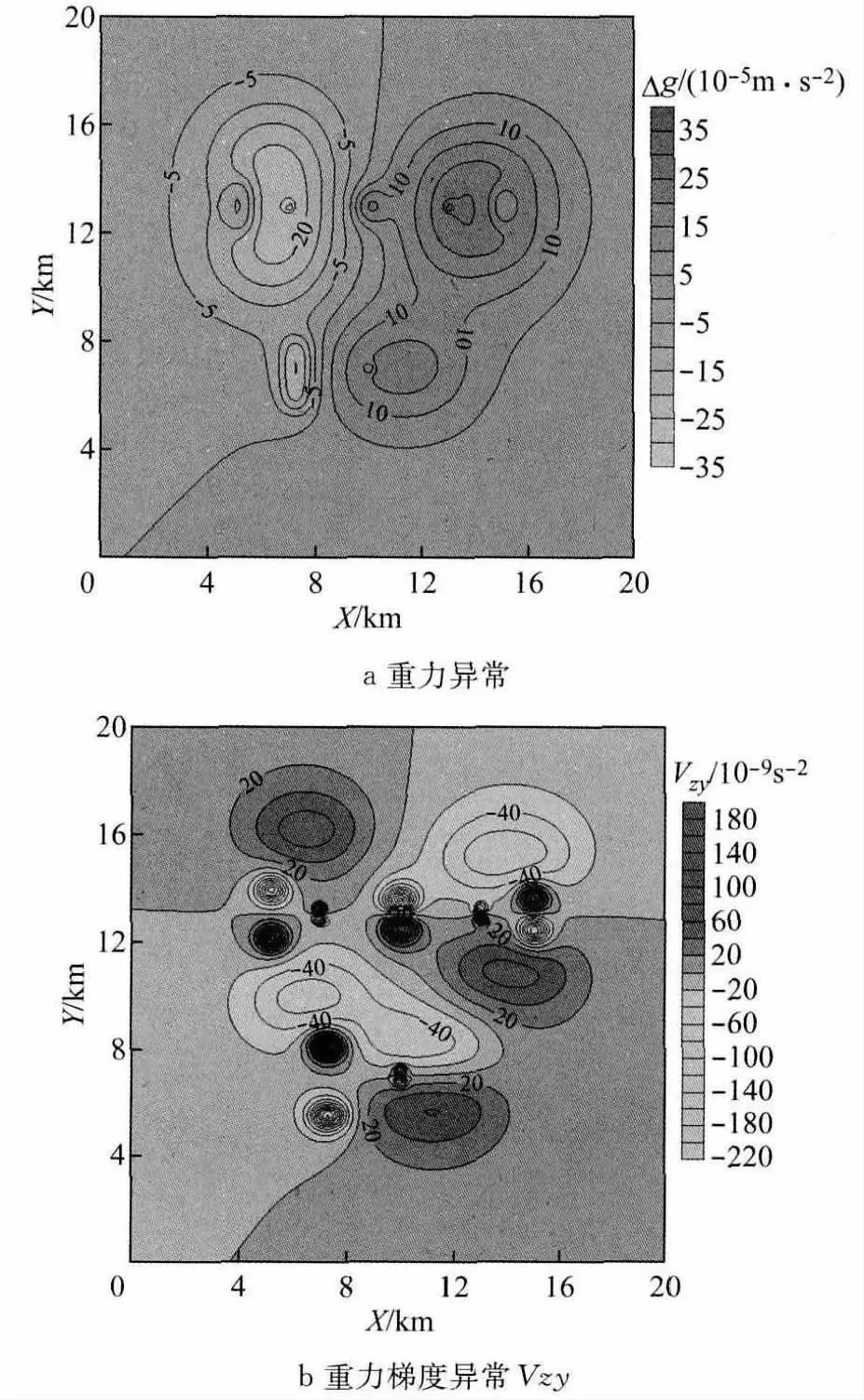
图3 重力异常及重力梯度异常图Fig.3 Gravity anomaly and gravity gradient anomaly map

3 重力场参数相关系数

3.1 断面重力场参数相关系数

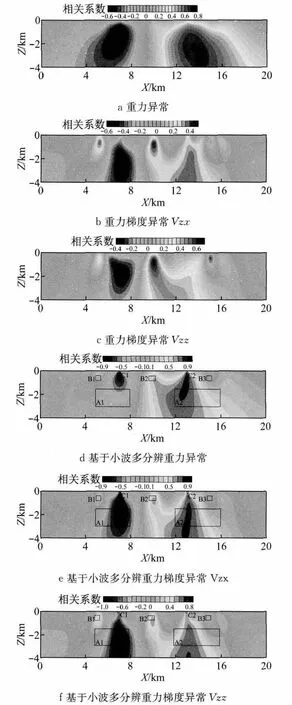
图4 Y＝13.0km处重力异常及重力梯度异常相关系数成像图Fig.4 Correlation coefficients imaging calculated by gravity anomaly and gravity gradient anomaly，Y＝13.0km

首先，选取模型Y=13.0km测线的重力异常/重力梯度异常曲线，求取其相关系数并成像，结果如图4所示.分析可知：①重力异常相关系数只能反映A1、A2这两个深层较大的异常；②Vzx相关系数基本上能反映所有异常体的基本情况；③Vzz相关系数能反映出A1、B1、B2和B3，对A2的反映较为模糊；④基于小波多分辨重力异常相关系数能清晰地反映 A2、B1、B2、B3、C1和C2，对 A1的反应不是很明显；⑤基于小波多分辨重力梯度异常Vzx相关系数准确地反映 A1、A2，B1、B2、B3、C1和 C2所有异常体的位置、深度以及剩余密度的正负；⑥基于小波多分辨重力梯度异常Vzz相关系数也准确地反映出A1、A2、B1、B2、B3、C1和C2所有异常体的位置、深度以及剩余密度的正负.

从以上分析结果可知，经过基于小波多分辨技术的重力异常分离后，成像准确度有明显提高.尤其是重力异常Δg，本来只能辨别A1和A2这两个大的异常，经过小波多分辨分解后，已经能辨别出所有异常体的分布情况，另外对Vzz的相关系数成像分辨率的提高也很明显.可见基于小波多分辨分析的相关系数在提高解释纵向和横向分辨率方面可行且有效.

3.2 小波函数及分解层数的选定

利用小波多分辨技术进行重力异常分离，重点是小波函数的选取.本文讨论使用较多且效果较好的几种小波函数，主要包括Haar小波、Daubechies小波系、Biorthogonal小波系、Coiflet小波系、Symlets小波系.判断一个小波的优劣主要根据处理结果和理论结果的误差ε大小.

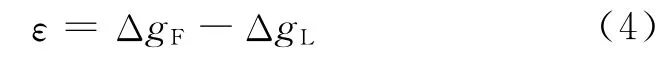
式中：ΔgF为重力异常Δg的分解值；ΔgL为Δg的理论计算值.

ε作为选定小波的依据，分别用重力异常Δg曲线和重力梯度异常Vzx曲线的分解结果与理论结果的分析比较，分别给出适合重力异常和重力梯度异常的小波函数.

对于重力异常Δg曲线，模型Y=13km剖面上的重力异常曲线如图5a所示，单独计算A1和A2在地面引起的异常值即理论异常值，如图5b所示，选取不同小波函数在剖面上的重力异常中分解出的A1和A2在地面引起的异常值即分解异常值，求取两者的误差值，可以得到各小波函数分解误差的大小，认为误差小的小波函数即为适合重力异常曲线分解的小波，表2给出其误差值.

表2给出了Haar小波、Daubechies小波系、Biorthogonal小波系、Coiflet小波系、Symlets小波系中的部分小波函数分解结果的误差值，从中可以看出，db8小波函数分解结果的误差值为3.729，明显小于其他小波函数分解结果的误差值.因此，认为db8小波函数最适应重力异常曲线，选定db8小波函数对重力异常数据进行多分辨分析.

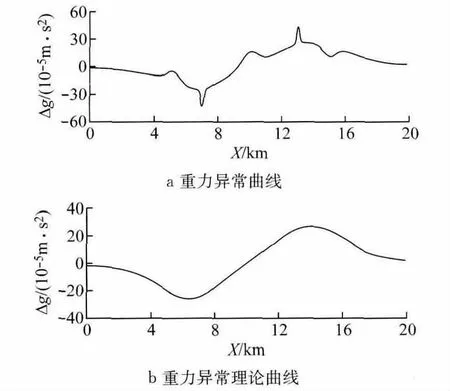
图5 重力异常理论曲线Fig.5 Theoretical curves of gravity anomaly

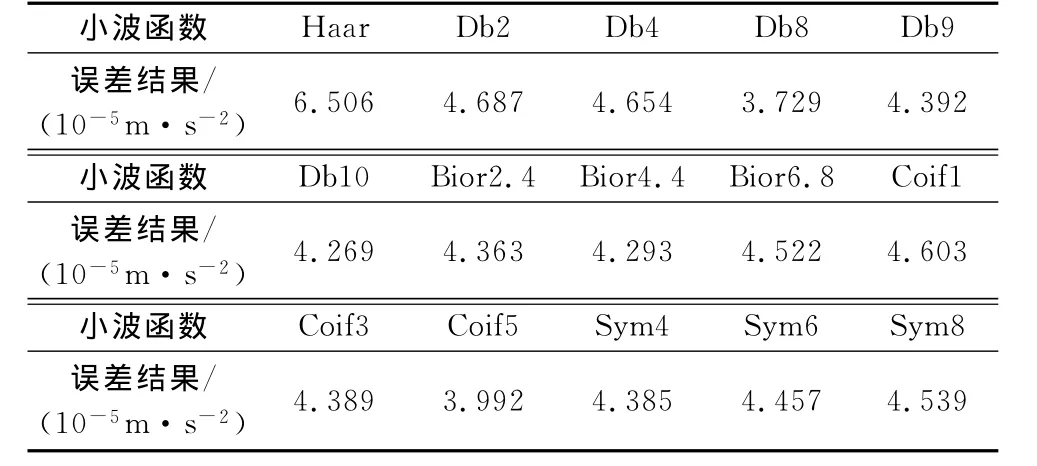
表2 不同小波函数重力异常分解结果误差值Tab.2 Error values of different wavelet function decomposition values of gravity anomaly

表3给出了Haar小波、Daubechies小波系、Biorthogonal小波系、Coiflet小波系、Symlets小波系中的部分小波函数Vzx分解结果的误差值，从中可以看出，db9、bior6.8和sym8小波函数分解结果的误差值相近，且远小于其他小波函数分解结果的误差值，但db9小波函数分解误差更小.认为db9小波函数最适应重力梯度异常曲线，选定db9小波函数对重力梯度异常数据进行多分辨分析.

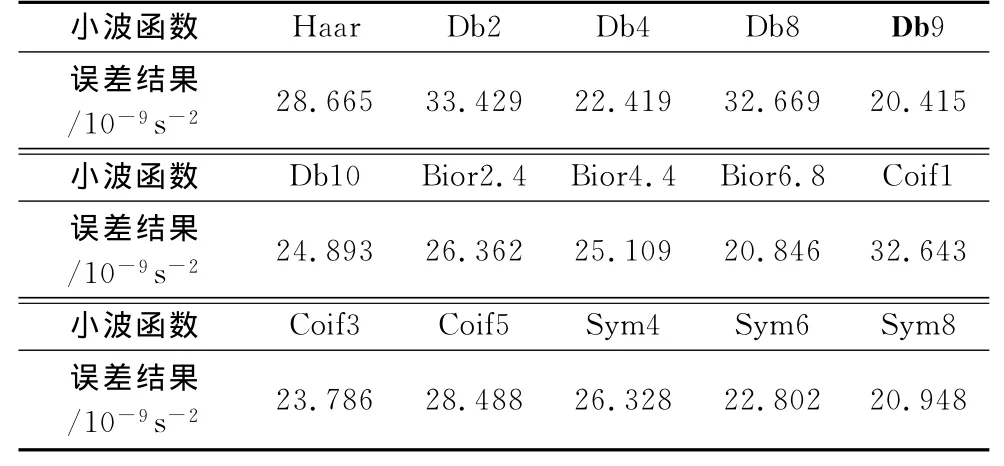
表3 不同小波函数Vzx分解结果误差值Tab.3 Error values of different wavelet function decomposition values of Vzx

小波分解阶数的选取依据下述规则：对于模型而言，如果某一阶分解结果最大值出现比上一阶分解结果最大值小两个数量级，就不再分解，认为分解结果是小波波形和模型数据曲线不一致造成的误差；对于实测数据而言，如果某一阶分解结果最大值小于实测时的观测均方误差值，就不再分解，认为分解结果是随机误差.

利用db8小波和db9小波分别对重力异常Δgq和重力梯度异常Vzx进行四阶分解，四阶低频逼近即为深层大范围的密度体引起的异常，三阶、四阶高频细节叠加就为中层中等范围的异常，一阶、二阶高频细节叠加就为浅层小范围的异常.将分解的重力异常和重力梯度异常求取相关系数并进行叠加，得到基于小波多分辨技术的相关系数结果如图4d～4f所示，对比图4a～4c和图4d～4f发现Vzx和Vzz在纵向和横向上对模型有一个比较好的分辨率，梯度异常的相关系数比之重力异常的相关系数分辨率更高.可以明显看出经过基于小波多分辨技术的重力异常分离后，成像准确度有明显提高.尤其是剩余重力异常Δgq，本来只能辨别两个大的异常，经过小波多分辨分解后，已经能辨别出所有异常体的分布情况，另外对Vzz的相关系数成像分辨率的提高也很明显.

4 模型结果

经过3.1节对选取测线重力数据相关系数的检验，利用基于小波多分辨分解的重力参数相关系数分析更加准确.用db8二维小波对平面重力异常进行分解以及db9二维小波对重力梯度异常Vzx进行分解，可以直观地发现已经能将异常分解成不同范围和量级的异常，将三维空间按100×100网格化，分解出的不同范围的局部异常，最后将相关系数叠加，最终重力异常和重力梯度异常Vzx相关系数成像结果如图6所示.

图6三维效果图和表1中模型的几何参数相比较，发现利用相关系数值圈定的异常曲面，能反映出模型各异常体的位置和范围，而且空间各点相关系数值的正负，表征了空间点剩余密度的正负，所以认为该种基于小波多分辨分析的重力/重力梯度异常相关系数成像方法取得了非常直观和清晰的结果.

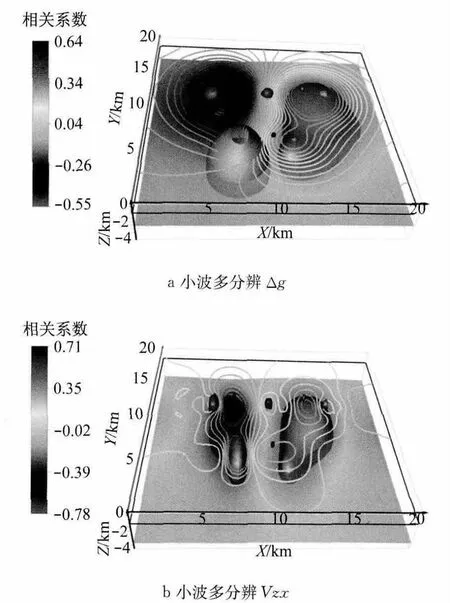
图6 基于小波多分辨的三维重力异常和重力梯度异常相关系数图Fig.6 Correlation coefficient map of gravity anomaly and gravity gradient anomaly based on wavelet multi-resolution

5 结论

本文是利用基于小波多分辨分析的相关系数方法对模型重力资料进行再处理，得出结论如下：

（1）重力梯度异常相关系数成像相比于重力异常相关系数成像具有更高的分辨率，这是因为重力梯度异常本身就是对重力异常的求导，相比重力异常更能突出异常位置.

（2）选取模型Y=13.0km剖面的重力参数，分别求取了未经小波多分辨分解的重力参数的相关系数值以及经过小波多分辨分解的重力参数的相关系数，并将它们的结果进行了对比分析.发现基于小波多分辨重力参数的相关系数在反映异常体的分辨率上有显著的提高，所以利用基于小波多分辨分解的重力参数计算相关系数是非常必要的.

（3）基于小波多分辨技术的模型重力异常三维相关系数成像结果，基本能反映出所有异常体的空间位置及分布情况，与模型参数对应良好，重力场参数相关系数成像效果明显.

［1］ 曾华霖.重力场与重力勘探［M］.北京：地质出版社，2005.ZENG Hualin.Gravity field and gravity exploration ［M］.Beijing：Geological Press，2005.

［2］ 霍志周.重力资料预处理系统研制［D］.西安：长安大学，2006.HUO Zhizhou.Study of pretreatment system of gravity data［D］.Xi’an：Chang’an University，2006

［3］ 许德树，曾华霖.优选延拓技术及其在中国布格重力异常图处理上的应用［J］.现代地质，2000，14（2）：215.XU Deshu， ZENG Hualin.Optimization continuation technology and its application of processing china bouguer gravity anomaly map［J］.Geosciences，2000，14（2）：215.

［4］ 曾华霖，许德树.最佳向上延拓高度的估计［J］.地学前缘.2002，9（2）：499.ZENG Hualin，XU Deshu.Estimate of the best upward continuation height［J］.Geoscience Frontiers，2002，9（2）：499.

［5］ 陈石.利用重力异常进行三维断层参数反演方法研究［D］.西安：长安大学，2005.CHEN Shi.Research on the inversion method of 3D fault parameters by gravity anomaly ［D］.Xi’an：Chang’an University，2005

［6］ Mauriello P，Patclla D.Principles of probability tomography for natural-sources electromagnetic induction fields ［J］.Goephysics，1999，64：1404.

［7］ Abdelrahman E M，Bayoumi A I，Abdelhady Y E.Gravity interpretation using correlation factors between successive least squares residual anomalies［J］.Geophysics，1989，54：1614.

［8］ 郭良辉，孟小红，石磊.重力异常分离的相关法［J］.地球物理学进展，2008，23（5）：1425.GUO Lianghui，MENG Xiaohong，SHI Lei.The correlation method for gravity anomaly separation ［J］.Progress in Geophysics，2008，23（5）：1425.

［9］ 陈召曦，孟小红，郭良辉.重磁数据三维物性反演方法进展［J］.地球物理学进展，2012，27（2）：503.CHEN Zhaoxi，MENG Xiaohong，GUO Lianghui.Review of 3D property inversion of gravity and magnetic data［J］.Progress in Geophysics，2012，27（2）：503.

［10］ 陈召曦，孟小红，郭良辉.基于GPU并行的重力、重力梯度三维正演快速计算及反演策略［J］.地球物理学报，2012，55（12）：4069.CHEN Zhaoxi，MENG Xiaohong，GUO Lianghui.Threedimensional fast forward modeling and the inversion strategy for large scale gravity and gravimetry data based on GPU［J］.Chinese Journal of Geophysics，2012，55（12）：4069.

［11］ 徐令周，关继腾，房文静.高次导数的概率成像原理［J］.青岛大学学报，2003，16（4）：32.XU Lingzhou，GUAN Jiteng，FANG Wenjing.Probability tomography theory of higher derivative［J］.Journal of Qingdao University，2003，16（4）：32.

［12］ 毛立峰，王绪本，高永才.大地电磁概率成像的效果评价［J］.地球物理学报，2005，48（6）：679.MAO Lifeng， WANG Xuben， GAO Yongcai.Effect evaluation of electromagnetic probability imaging［J］.Chinese Journal of Geophysics，2005，48（6）：679.

［13］ 杨文采，施志群，侯遵泽.离散小波变换与重力异常多重分解［J］.地球物理学报，2001，44（4）：534.YANG Wencai，SHI Zhiqun，HOU Zhunze，et al.Discrete wavelet transform and gravity anomalies multiple decomposition［J］.Chinese Journal of Geophysics，2001，44（4）：534.