无穷直线上非齐次2阶方程的Riemann边值问题
2014-02-16曾伟
曾伟
(西南民族大学预科教育学院, 四川 成都 610041)
曾伟
(西南民族大学预科教育学院, 四川 成都 610041)
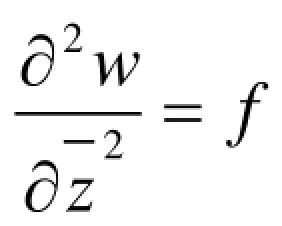
双解析函数; 非齐次; Riemann边值问题; 可解性定理.
引言
解析函数论作为一种有用的工具,已被广泛的应用于天体力学、弹性力学、理论物理等方面. 维库阿在文[1]中提出并研究了广义解析函数.赵桢在文[2]中,提出并初步研究了双解析函数,阐明了双解析函数的理论意义及其物理背景和实际应用. 王明华在文[3-4]中给出了双解析函数的某些性质,提出并研究了Cauchy-Fredholm型积分,给出了双解析函数的Hilbert边值问题;给出了双解析函数在无穷直线上的Riemann边值问题的可解性定理[5-11].本文首先进一步研究了双解析函数的平均值定理、无穷可微性、Cauchy不等式和Liouville定理.然后对双解析函数在无穷直线上的非齐次2阶方程的Riemann边值问题进行了研究.
1 双解析函数的性质



2 无穷直线上非齐次2阶方程的Riemann边值问题


[1] 维库阿·依·涅.广义解析函数[M]. 中国科学院数学研究所译.北京: 人民教育出版社, 1960.
[2] 赵桢. 双解析函数与调和函数以及它们的基本边值问题[J]. 北京师范大学学报: 自然科学版, 1995, 61(2): 175-179.
[3] 王明华. 无穷直线上的双解析函数的Riemann边值问题[J]. 宁夏大学学报: 自然科学版, 2003, 24(3): 249-251.
[4] 王明华. 双解析函数的性质及Hilbert边值问题[J]. 北京师范大学学报: 自然科学版, 1998, 34(1): 13-20.
[5] 杨丕文. k-正则函数及其某些边值问题[J]. 四川师范大学学报: 自然科学版, 2001, 24(1): 5-8.
[6] 杨丕文. 正则向量函数及某些函数论性质[J]. 四川师范大学学报: 自然科学版, 1999, 22(4): 359-364.
[7] 曾伟. 无穷直线上双解析函数的一类非正则型边值问题[J]. 西南民族大学学报:自然科学版, 2013, 39(4): 554-559.
[8] 杨柳. k-正则函数的性质及其Riemann边值问题和它的反问题[J]. 四川师范大学学报: 自然科学版, 2005, 28(1): 39-42.
[9] 闻国椿. 共形映射与边值问题[M]. 北京: 高等教育出版社, 1985.
[10] 李子值等. 函数论的边值问题[M]. 河北: 河北大学出版社, 2000.
[11] 路见可. 解析函数边值问题[M]. 上海: 上海科学技术出版社, 1987.
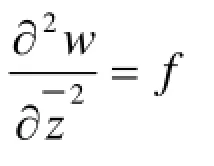
ZENG Wei
(School of Preparatory Education, Southwest University for Nationalities ,Chengdu 610041, P.R.C.)
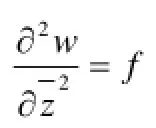
bianalytic function; Inhomogeneous; Riemann boundary value problem; solvability
O174.55
: A
: 1003-4271(2014)03-0394-05
10.3969/j.issn.1003-4271.2014.03.12
2014-04-02
曾伟(1980-), 男, 讲师, 硕士, 研究方向:复偏微分方程的边值问题.邮箱:zw0830@163.com.基金项目:西南民族大学2014年校级科研项目(2014NZYQN49)
