塑性扩容梯度对孔隙介质岩体中T-H-M耦合作用的二维有限元分析

张玉军，张维庆

（1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2.中铁隧道勘测设计院有限公司，天津 300133）

1 引言

对于承受压力作用的岩体，随着荷载的增加，其体积变形要经历压缩、扩容（剪胀）、溃散等阶段。关于岩体的扩容，人们已进行了相当多的研究[1－10]。金济山[11]研究了扩容应变和扩容体应变的变化，并给出了本构方程，用该理论做出的数值模拟结果与岩石力学试验的结果比较吻合。侯文诗等[12]通过对8种岩样的单轴、三轴压缩试验结果分析，获得低围压下的应力–体积应变曲线，揭示了岩石扩容起始特性与峰值点特性的对应关系。段艳燕等[13]认为，岩石的剪胀非微观结构的产生、扩展和汇集，其实质为岩石内部组构特征发生了显著的变化，是破裂块体之间镶嵌组合的一种结构效应，剪胀变形要比质点连续移动的弹塑性变形量大得多。阎岩等[14]通过渗流-流变耦合试验显示，在低应力作用下试件体积不断缩小，渗透系数也随之减小，应力增大到某值后体积逐步扩大而出现扩容，渗透系数也随之增大。张玉军等[15]在所建立的热–气–应力(T-H-M)耦合弹塑性模型中，尝试将岩体的孔隙率和渗透性作为平均有效应力和剪胀体积应变的函数，以一个假定的地质结构为考察对象，对CO2注入过程中岩体内的热-气-应力耦合现象进行了有限元计算分析。

然而，迄今为止对于岩体的扩容及相伴效应（如渗透系数增加）的研究还主要限于室内试验和理论建模，在数值模拟方面的应用尚相当少，故相应的现象和规律的揭示还很不充分。鉴于此，笔者以一个假定的位于饱和单一孔隙地层中的高放废物地质处置库实验室尺度模型为算例，在相同的初始温度和岩体应力条件下，基于Mohr-Coulomb屈服准则，针对考虑塑性扩容梯度对岩体孔隙率及渗透系数影响不同的5种计算工况，进行热-水-应力耦合有限元数值模拟，考察了处置库近场的温度、孔隙率和渗透系数、孔隙水压力、地下水流速、应力的变化、分布情况，得出了一些新的认识。

2 孔隙介质热-水-应力耦合方程

对于单一孔隙介质，笔者建立了一种热-水-应力耦合模型(由相应的双重孔隙—裂隙介质模型退化而来)[16]，控制方程如下。

（1）应力平衡方程

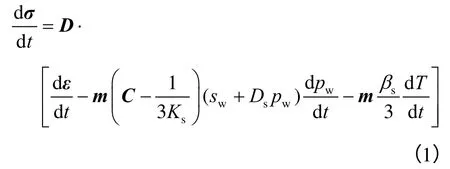
应力平衡方程为式中：σ、ε 分别为应力和应变；D=C-1为弹性矩阵；mT=[1 1 0]为法向应力单位列阵；Ks、βs、T 分别为孔隙介质的体积模量、热膨胀系数和温度；sw、pw、Ds、C 分别为孔隙介质的饱和度、水压力、湿气容量和柔度矩阵；t为时间。

（2）水连续性方程

根据质量守恒原理，在dt 时段内流入某一物体的水量应等于其内部储水量的增加。设定水的渗流可以用达西定律来描述，则有

式中：k、krw分别为孔隙介质的固有渗透率张量和比渗透率；ρw、μw、γw依次为水的密度、黏滞系数和重度；z为位置水头；Dt为孔隙介质的温度梯度水分扩散系数；A、B、F 均为常数项表达式。

（3）能量守恒方程

根据能量守恒原理，在dt 时段内流入某一物体的热量应等于其内能的增加，可得

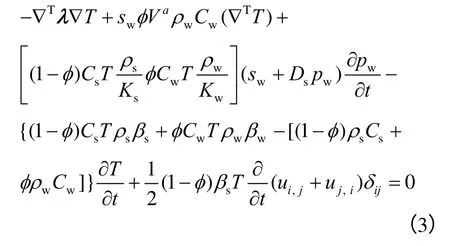
式中：Cw、Cs分别为水及孔隙介质的比热；φ、ρs、λ 分别为孔隙介质的孔隙率、密度和导热系数矩阵；Va为孔隙水的平均表观流速； ui、 uj为位移分量；δij为克罗内克符号。

3 弹塑性分析

弹塑性计算时有效应力增量可表示为

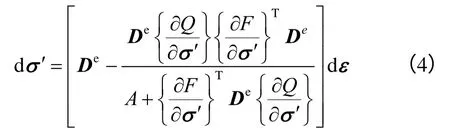
式中：σ′、ε 分别为效应力列阵和应变列阵；De为弹性矩阵；A为硬化参数；Q、F 分别为塑性势及屈服函数。

当Q=F 时，称为相关联的流动法则；当Q ≠F时，称为不相关联的流动法则。

本程序中使用相关联的流动法则，并令A=0，取Mohr-Coulomb准则为屈服函数[[17]，即

其中：

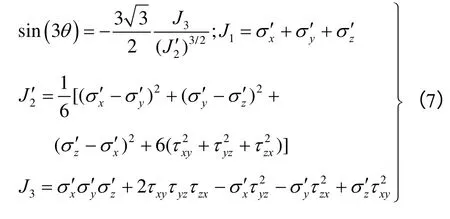
4 孔隙率-渗透系数演化律

图1、2为根据试验得出的岩石应力-应变全过程曲线及体积应变与渗透系数的关系。图1中，A、B、C 依次对应于为轴向、径向及体积应变）。

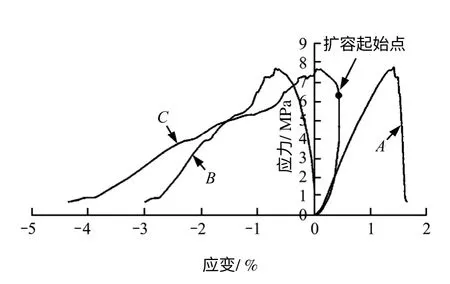
图1 应力-应变全过程曲线[12]Fig.1 Full relationships between stress and strain[12]

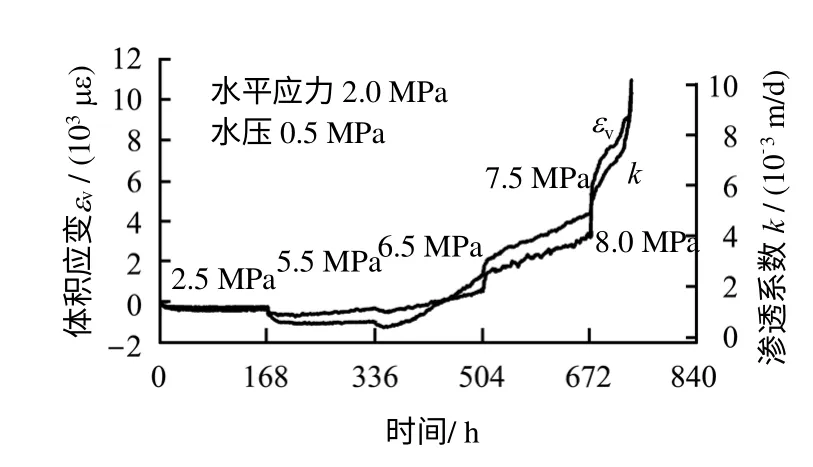
图2 体积应变-渗透系数的关系[14]Fig.2 Relationships between volumetric strain and permeability coefficient[14]

需要指出，本文中的“塑性扩容”是指岩体的“破裂”或“破碎”阶段，此时实际岩体已是非连续介质，其内部组构特征发生了显著的变化，剪胀变形要比质点连续移动的弹塑性变形量大得多[13]，用塑性力学（连续介质、剪胀角等概念）已不能很好地描述其特性，故引用和扩展了马士进提出的岩体扩容与最大主应变的线性关系式，这是一种经验处理。

马士进[18]提出，在单轴压缩条件下（围压σ3=0）岩体扩容与最大主应变可以简化成线性关系：

式中：ΔV、V 分别为岩体的扩容体积增量和初始体积；ε1为最大主应变；η为扩容梯度。

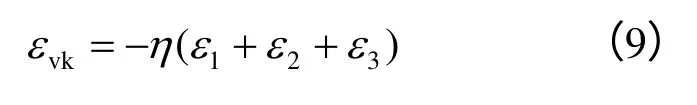
马士进根据Price的实验，认为岩体扩容梯度并非常数，而是和岩体组成、侧压系数（σ2、σ3不为0）等有关。但在计算中，为简化问题，马士进取η为定值[18]。笔者在本文的数值模拟中，也取η为常数，但考察η 的变化对计算结果的影响。

当假设岩体的固体颗粒为不可压缩时，近似地有Δεvk=Δφ[19]，从而将Taron等[20]给出的孔隙率表达式修正为

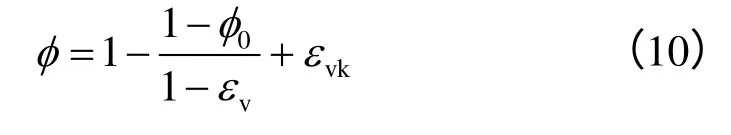
式中：εv为弹塑性体积应变；φ0为初始孔隙率。

由此可求出对应的渗透系数[21]为

式中：k0为初始时刻的渗透系数。

将上述单一孔隙介质热-水-应力耦合模型及孔隙率-渗透系数演化律引入笔者所研制的二维有限元程序中[22]，其计算步骤为

①开始时，孔隙率、渗透系数和其他参数取初值。

②经 ti=Δt 时段的弹性或弹塑性T-H-M耦合分析后，得出相应的温度场、渗流场和应力场。

③针对塑性岩体单元，计算扩容体积应变，求出新的孔隙率、渗透系数和其他参数。

5 算 例

如图3所示，此为一实验室尺度的核废料玻璃固化体埋置模型，其周围的介质是饱和的孔隙岩体。作为近似简化，认为这是一个平面应变问题。取计算域的范围为水平向4 m，垂直向8 m，有800个单元，861个节点。玻璃固化体为矩形，其尺寸为0.4 m×0.4 m、中心的坐标x=y=0（y 轴向下为正）。从固化体边缘向右的点号依次为432、433、434、435、436。

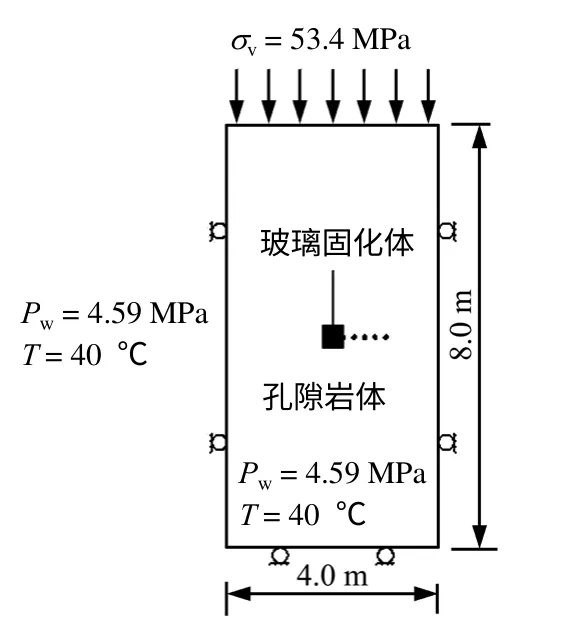
图3 计算模型Fig.3 Computation model

对于边界条件，计算域的顶面位移自由，其上作用有分布荷载53.4 MPa，左、右侧面的水平方向位移约束，底面的垂直方向位移约束，所有边界的温度为40 ℃，各边界的孔隙水压力均为4.59 MPa，岩体的初始孔隙率为0.1。热-水-应力耦合的环境对岩体介质要产生塑性扩容作用，从而引起孔隙率和渗透系数的变化。有关的计算参数见表1。取玻璃固化体为弹性体，而岩体的黏聚力和内摩擦角分别为c=12.0 MPa和φ=35°。初始状态时，岩体的温度均为40 ℃。核废物以1 000 W的不变功率释放热量，时间经历了4年。

岩体介质的水分特性曲线符合Van Genuchten模型[23]，即

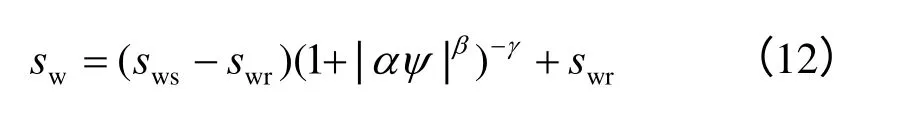
式中：α=3.86×10-6m-1，β=1.41，γ=1 -1/β；ψ为水势；sws=1.0，swr=0.19，其分别为最大饱和度和最小饱和度。

表1 主要计算参数Table 1 Main computation parameters

比渗透率与饱和度的关系为

参照文献[18]中的参数敏感性分析，设定了5种工况：扩容梯度η 依次为0.0、1.0、1.5、2.0、2.5。主要结果及分析如下:由于渗流和地应力对核废物释热的影响较小[24]，故5种工况条件下计算域中的温度场基本相同。以工况1为例，432、433、434、435各点处的温度随时间的变化曲线如图4所示。由图可见，开始约0.1年内岩体的温度快速上升，之后增加减缓，到计算终了时432、433、434、435各点的温度依次为97.8、81.9、72.6 ℃和65.7 ℃。图5为工况1在4年时计算域中的温度等值线分布。

由图6可见，各工况的计算域中应力量值及分布产生了一定差别，如到4年时432、434点水平正应力(MPa)/垂直正应力(MPa)依次为，工况1：-10.334/-32.079、-14.484/-35.332；工况2：-10.386/32.100、-14.515/-35.362；工况3：-10.455/-32.084、-14.553/-35.376；工况4：-10.575/-32.032、-14.610/35.384；工况5：-10.710/-31.929、-14.677/-35.388。到4年时岩体中塑性区见图7，其分布大致呈竖立的哑铃形，而工况1～5的塑性区面积依次为12.28、13.28、13.56、14.20 m2和14.92 m2。由此可知，随着岩体扩容梯度η 的增加，岩体中的应力量值及塑性区面积均上升。

图4 温度-时间曲线Fig.4 Curves of temperatures vs.time

图5 4年时工况1计算域中温度等值线（单位：℃）Fig.5 Temperature contours in calculation domain at 4 years(unit:℃)

图8为到4年时岩体中孔隙率增量(φ4y-φ0)等值线分布。由图可见，相比于不考虑扩容的工况1，其余考虑扩容的工况有很大的差别不同，特别是在弹、塑区的交界处有显著的等值线集中现象，具有某种“剪切带效应”，并且考虑扩容的各工况也依各自的扩容梯度不同，其孔隙率增量等值线的量值和分布也有所变化。此时在固化体中心正下方y为0.3 m和1.1 m处的孔隙率对于工况1～5依次为：0.100 535、0.100 687，0.100 537、0.112 463 9，0.100 539、0.137 618，0.100 541、0.149 020，0.100 541、0.163 456，均比初始值0.1升高。但因y为0.3 m和1.1 m处分别位于弹性区和塑性区，只有在塑性区才产生体积扩容并计入其对孔隙率的影响，故塑性区的孔隙率相比于其初始值有明显增长，并且随所取扩容梯度值的变大，各工况的孔隙率也逐渐上升。上述两点处的孔隙率增量随时间的变化曲线如图9所示。

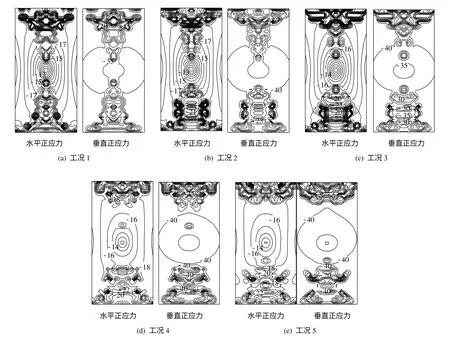
图6 4年时计算域中正应力等值线（单位：MPa）Fig.6 Normal stress contours in calculation domain at four years(unit:MPa)

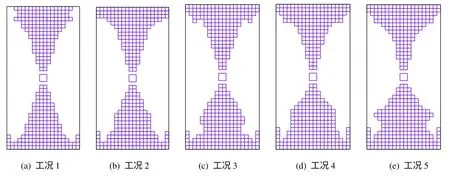
图7 4年时计算域中塑性区Fig.7 Plastic zones in calculation domain at four years

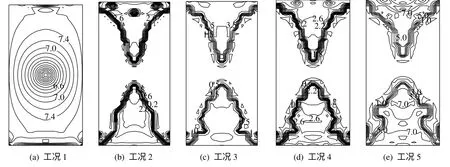
图8 4年时岩体中孔隙率增量等值线（工况1，单位：10-4，工况2～5，单位：10-2）Fig.8 Contours of porosity increment in rock mass at four years（unit is 10-4 for case 1，and 10-2 for cases 2-5）

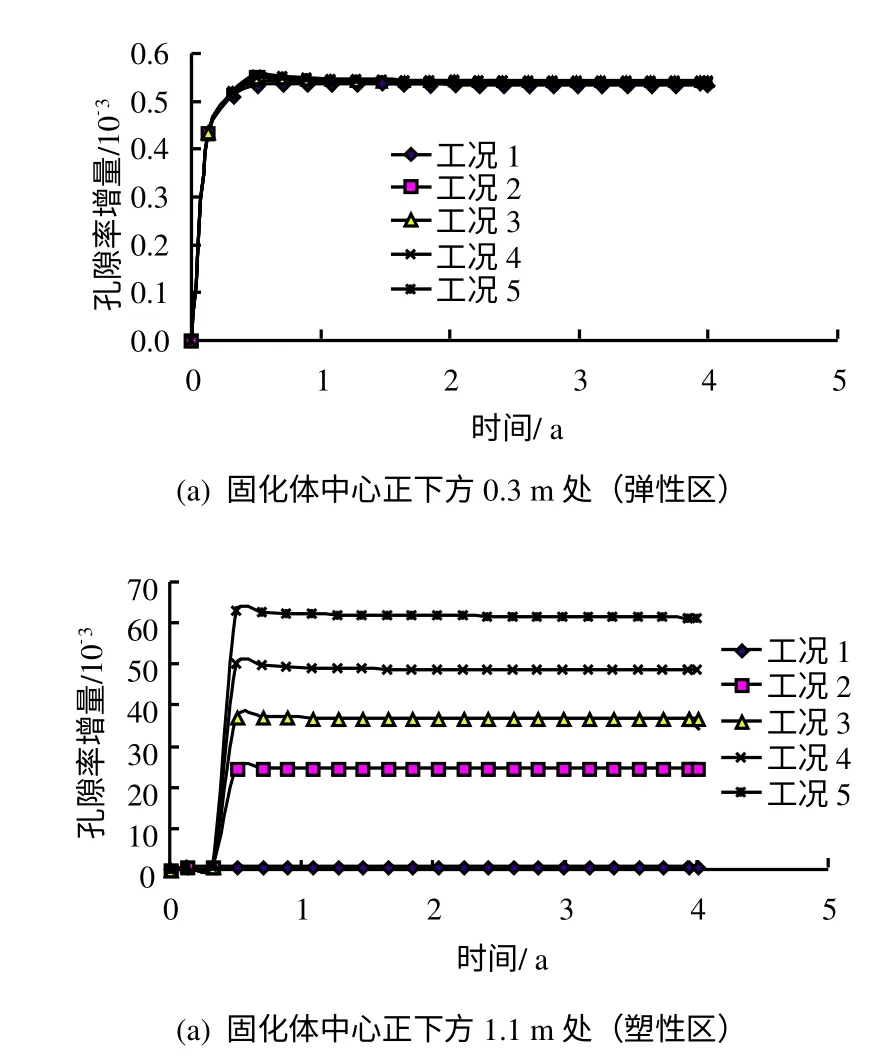
图9 岩体中2个点的孔隙率增量与时间曲线(固化体中心y=0)Fig.9 Porosity increments vs.time at two nodes(y=0 at the center of vitrified waste)

由图9可知，开始约0.6年内，因玻璃固化体的急剧释放热量和岩体上覆及自重荷载的施加，使得岩体孔隙率增量内快速上升，之后随时间的推移孔隙率增量虽有所下降，但变化幅度较小（渐趋平衡），并且对于不同的扩容梯度值，孔隙率增量在弹性区变化不大，而在塑性区却有明显差别。

相对应的渗透系数增量的等值线分布及随时间的变化曲线分别见图10、11。其与孔隙率增量的演化规律类似，在时间上表现了一定的非线性特征。上述两点处的渗透系数对于工况1～5依次为：1.261 51×10-13、1.267 01×10-13m/s；1.261 61×10-13、2.538 00×10-13m/s；1.261 67×10-13、3.463 31×10-13m/s；1.261 75×10-13、4.533 29×10-13m/s；1.261 77×10-13、5.994 23×10-13m/s。由图中也看到，固化体中心正下方y=1.1 m处进入塑性区之后该点渗透系数也比弹性时有明显的增加（体积扩容的作用）。

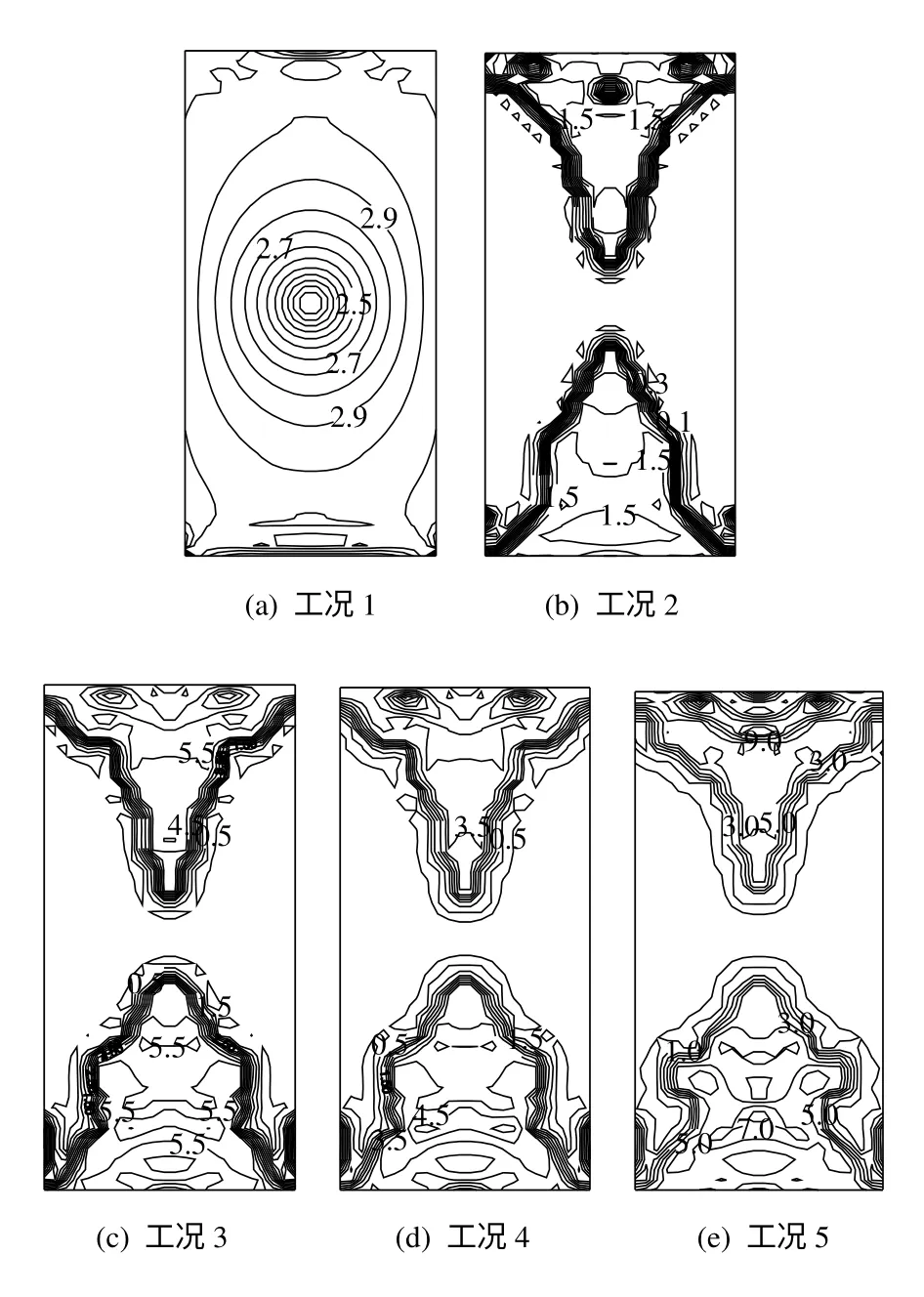
图10 4年时岩体中渗透系数增量等值线（工况1，单位：10-15 m/s，工况2～5的单位：10-13 m/s）Fig.10 Contours of permeability increment in rock mass at four years（unit is 10-15 m/s for case 1，and 10-13 m/s for cases 2-5）

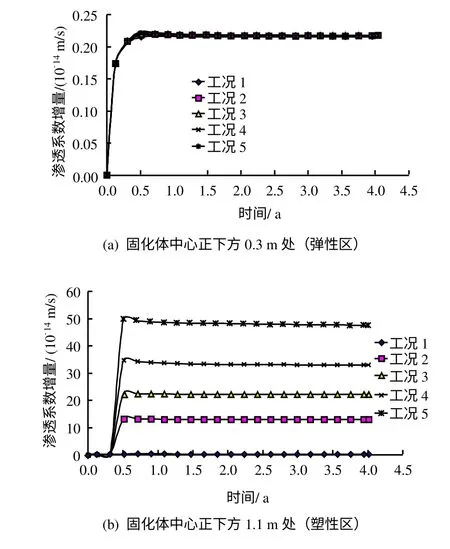
图11 岩体中2个点的渗透系数增量与时间曲线(固化体中心y=0)Fig.11 Permeability increments vs.time at two nodes(y=0 at the center of vitrified waste)

图12为在固化体中心正下方y=0.3、1.1 m处的孔隙水压力随时间的变化曲线。

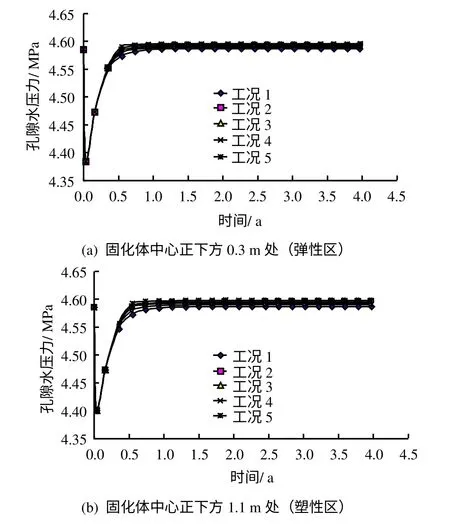
图12 岩体中两个点的孔隙水压力-时间曲线Fig.12 Pore pressures vs.time at two nodes for two cases

由图12可见，一开始由于岩体荷载的突然施加，孔隙水压力有瞬时的少许下降，之后在应力场和温度场的共同作用下，孔隙水压力随时间呈现一定幅度的上升。到4年时该两点处的孔隙水压力值对于工况1～5为：4.587 01、4.587 02，4.589 31、4.590 40，4.591 22、4.592 64，4.593 45、4.595 37，4.595 92、4.597 88 MPa。弹性区和塑性区的孔隙水压力无明显差别，其原因在于弹性区和塑性区是水力连通的，两区的孔隙水压力随时间趋于平衡。同时也比较可知，随所取扩容梯度值的变大，各工况的孔隙水压力也有所上升（仅管幅度很小）。计算终了时两种工况中的孔隙水压力等值线如图13所示。

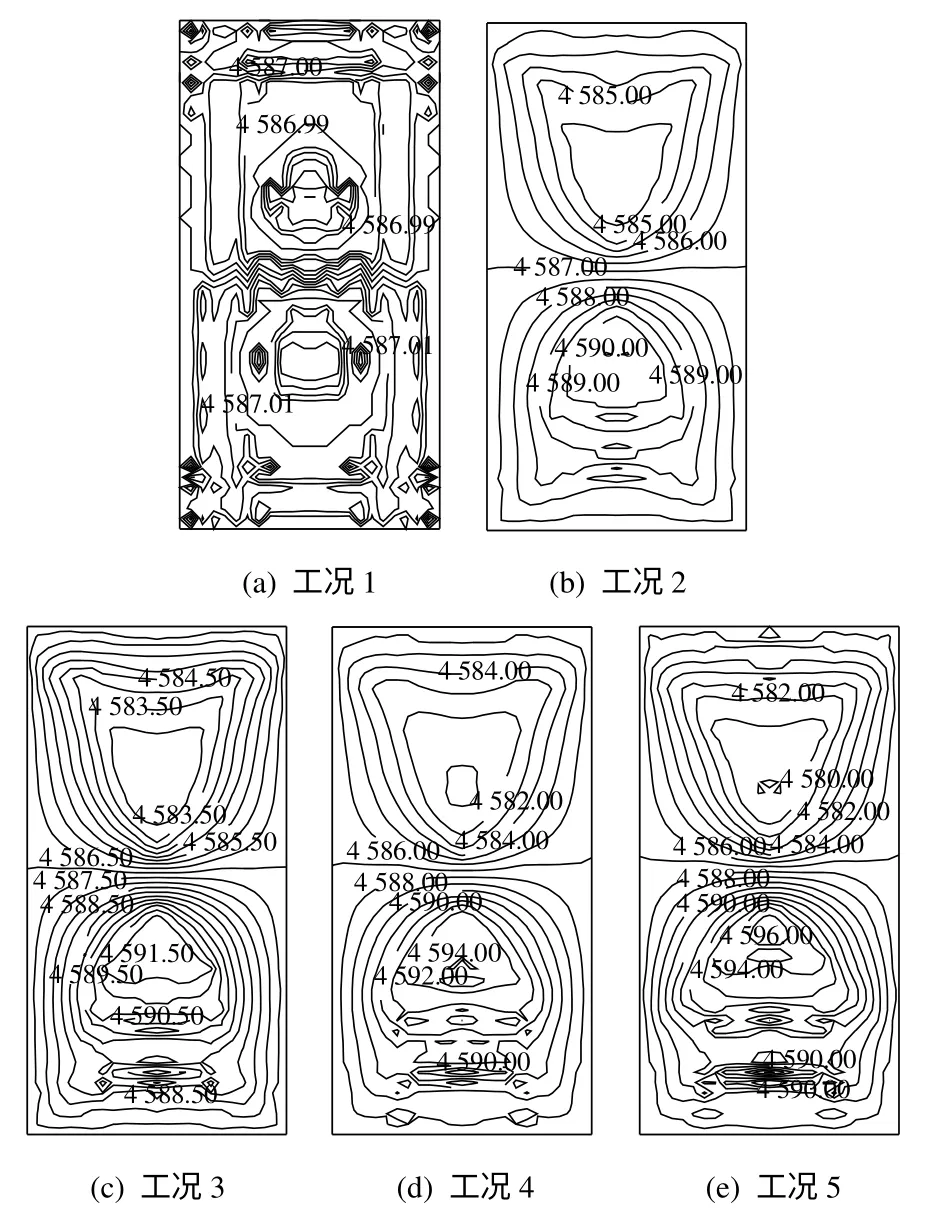
图13 4年时岩体中的孔隙水压力等值线(单位：kPa)Fig.13 Contours of pore pressures in rock mass at four years(unit:kPa)

由图13可见，大致以过玻璃固化体中心的水平线为分界，在其上、下方形成了2个孔隙水压力等值线族闭合环，与哑铃形的塑性区对应。并且随所取扩容梯度值的改变，各工况的孔隙水压力等值线的量值和分布亦呈现一定的差别。

图14为各工况在4年时计算域中的孔隙水流速矢量分布，工况1与其他工况的比例为500:1。由图可见，其与塑性区的分布有一定的对应关系，并且随着所取扩容梯度值的增加，孔隙水流速矢量也逐渐变大。在固化体中心正下方y=0.3、1.1 m处，到4年时该2点处的孔隙水流速矢量对于工况1～5依次为：6.81×10-12、2.15×10-12，6.18×10-10、1.22×10-10，1.04×10-9、1.08×10-11，1.54×10-9、9.48×10-10，2.04×10-9、6.41×10-9m/s 。

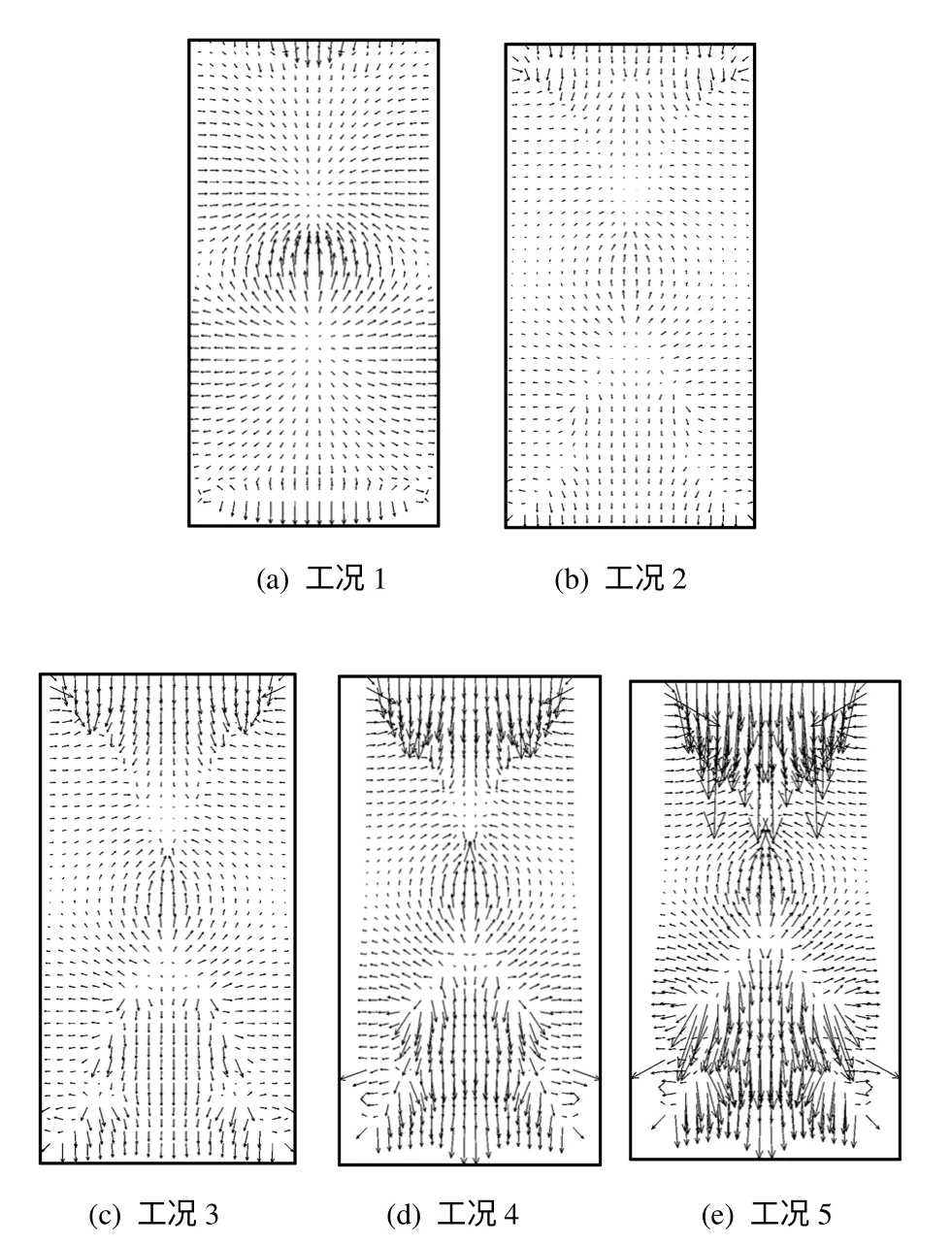
图14 4年时计算域中的孔隙水流速矢量Fig.14 Flow vectors of pore water in calculation domain at four years for two cases

6 结语

笔者针对其所建立的双重孔隙—裂隙介质热-水-应力（T-H-M）耦合模型，经退化处理，得出了相应的单一孔隙介质热-水-应力耦合模型，并引入岩体扩容梯度，使用Mohr-Coulomb准则，计入塑性扩容对岩体孔隙率及渗透系数影响，以一个假定的实验室尺度且位于饱和孔隙岩体中的高放废物地质处置模型为例子，就不同的扩容梯度值进行了5种工况的热-水-应力耦合的二维有限元模拟，考察了岩体中的温度、正应力、塑性区、孔隙率及渗透系数、孔隙水压力和地下水流速的变化、分布情况。计算结果表明，两种工况中的温度状态基本相同，计算终了的4年时，岩体近场的温度可达到40.0～98.0 ℃；塑性区的分布大致呈竖立的哑铃形；相比于不考虑扩容梯度的工况1，其余工况的正应力、孔隙率及渗透系数、孔隙水压力和地下水流速等的分布与塑性区的分布有明显的对应关系，呈现了某种“剪切带效应”；正应力量值、塑性区面积、孔隙率及渗透系数、孔隙水压力、地下水流速等均随所取扩容梯度值的变大而增加。

[1]COOK N G W.An experiment proving that dilatancy is a pervasive volumetric property of brittle rock loaded to failure[J].Rock Mechanics，1970，2:181－188.

[2]陈宗基，康文法.在岩石破坏和地震之前与时间有关的扩容[J].岩石力学与工程学报，1983，2(1):11－21.TAN Tjiong-kie，KANG Wen-fa.Time dependent dilatancy prior to rock failure and earthquakes[J].Chinese Journal of Rock Mechanics and Engineering，1983，2(1):11－21.

[3]陈宗基，石泽全，于智海，等.用8 000 kN多功能三轴仪测量脆性岩石的扩容、蠕变及松弛[J].岩石力学与工程学报，1989，8(2):97－118.TAN Tjiong-kie，SHI Zhe-quan，YU Zhi-hai，et al.Dilatancy creep and relaxation of brittle rocks measured with the 8 000 kN multipurpose triaxial apparatus[J].Chinese Journal of Rock Mechanics and Engineering，1989，8(2):97－118.

[4]陈宗基，康文法.岩石的封闭应力、蠕变和扩容及本构方程[J].岩石力学与工程学报，1991，10(4):200－312.TAN Tjiong-kie，KANG Wen-fa.On the locked in stress，creep and dilatation of rocks，and the constitutive equations[J].Chinese Journal of Rock Mechanics and Engineering，1991，10(4):200－312.

[5]许东俊，李小春.应力状态和岩石扩容特性[J].岩土力学，1992，13(2):11－21.XU Dong-jun，LI Xiao-chun.Stress path and dilatancy behavior of rocks[J].Rock and Soil Mechanics，1992，13(2):11－21.

[6]康红普.岩石扩容与巷道底臌[J].矿业快报，1992，11(3):15－17.KANE Hong-pu.Rock dilatancy and opening floor heave[J].Express Information of Mining Industry，1992，11(3):15－17.

[7]MAHMUTOGLU Y，VARDAR M.Effects of inelastic volume increase on fractured rock behaviour[J].Bull Eng.Geol.Env.，2003，62:117－121.

[8]YUAN SHINCHE，HARRISON J.An empirical dilatancy index for the dilatant deformation of rock[J].International Journal of Rock Mechanics and Mining Sciences，2004，41:679－686.

[9]李林峰，侯克鹏，余贤斌，等.岩石峰后扩容特性及扩容模型的探讨[J].矿业快报，2007，26(9):15－17.LI Lin-feng，HOU Ke-peng，YU Xian-bin，et al.Study of rock dilatancy characteristic and dilatancy model after peak stress[J].Express Information of Mining Industry，2007，26(9):15－17.

[10]张长科，李林峰.岩石峰值应力后扩容与围压的关系[J].有色金属，2009，61(4):134－137.ZHANG Chang-ke，LI Lin-feng.Study on relation between rock post-peak dilatancy and confining pressure[J].Nonferrous Metals，2009，61(4):134－137.

[11]金济山.岩石扩容性质及其本构模型的研究[J].岩石力学与工程学报，1993，12(2):162－172.JIN Ji-shan.Study of the dilatancy behavior of rocks and its constitutive model[J].Chinese Journal of Rock Mechanics and Engineering，1993，12(2):162－172.

[12]侯文诗，李守定，李晓，等.岩石扩容起始特性与峰值特性的比较[J].岩土工程学报，2010，32(5):657－660.HOU Wen-shi1，LI Shou-ding，LI Xiao，et al.Comparison between the dilatancy onset and the peak of different rocks[J].Chinese Journal of Geotechnical Engineering，2010，32(5):657－660.

[13]段艳燕，宋宏伟.岩石峰后剪胀效应研究综述[J].地下空间与工程学报，2007，3(6):1027－1030.DUAN Yan-yan，SONG Hong-wei.Review of dilatancy nature of the rock post-failure behaviour[J].Chinese Journal of Underground Space and Engineering，2007，3(6):1027－1030.

[14]阎岩，王恩志，王思敬，等.岩石渗流-流变耦合的试验研究[J].岩土力学，2010，31(7):2095－2103.YAN Yan，WANG En-zhi，WANG Si-jing，et al.Study of seepage-rheology coupling experiment of rocks[J].Rock and Soil Mechanics，2010，31(7):2095－2103.

[15]张玉军，张维庆.孔隙率的应力–剪胀依存性对CO2地层注入热-气-应力耦合影响的数值分析[J].岩石力学与工程学报，2010，29(9):1774－1781.ZHANG Yu-jun，ZHANG Wei-qing.Numerical analysis of influence of stress-dilatancy dependence of porosity on thermo-gas-mechanical coupling in CO2injection in stratum[J].Chinese Journal of Rock Mechanics and Engineering，2010，29(9):1774－1781.

[16]张玉军.遍有节理岩体的双重孔隙-裂隙介质热-水-应力耦合模型及有限元分析[J].岩石力学与工程学报，2009，28(5):947－955.ZHANG Yu-jun.Coupled thermo-hydro-mechanical model and finite elementanalyses of dual-porosity fractured medium for ubiquitous-joint rock mass[J].Chinese Journal of Rock Mechanics and Engineering，2009，28(5):947－955.

[17]OWEN D，HINTON E.Finite element in plasticity:Theory and practice[M].Swansea U.K.:Pineridge Press Limited，1980，

[18]马士进.软岩巷道围岩扩容软化变形分析及模拟计算[D].辽宁:辽宁工程技术大学，2001.

[19]RUTQVIST J，BÖRGESSON L，CHIJIMATSU M，et al.Thermo-hydro-mechanics of partially saturated geological media:governing equations and formulation of four finite element models[J].International Journal of Rock Mechanics and Mining Sciences，2001，38(1):105－127.

[20]TARON J，ELSWORTHD.Constraints on compaction rate and equilibrium in the pressure solution creep of quartz aggregates and fractures:Controls of aqueous concentration[J].Journal of Geophysical Research，2010，Vol，115:B07211.doi:10.1029/2009JB007118.

[21]LEE D，ELSWORTH D，YASUHARA H，et al.Experiment and modeling to evaluate the effects of proppant-pack diagenesis on fracture treatments[J].Journal of Petroleum Science and Engineering，2006，74:67－76.

[22]张玉军.废料地质处置近场热-水-应力-迁移耦合二维有限元分析[J].岩土工程学报，2007，29(10):1553－1557.ZHANG Yu-jun.2D FEM analysis for coupled thermohydro-mechanical-migratory process in near field of geological disposal of nuclear waste[J].Chinese Jounal of Geotechnical Engineering，2007，29(10):1553－1557.

[23]CHIJIMATSU M，KURIKAMI H，ITO A，et al.Implication of T-H-M coupling on the near-field of a nuclear waste repository in a homogeneous rock mass[R].Tokyo:Hazama Corporation，2002：1－43.

[24]RUTQVIST J，CHIJIMATSU M，JING L，et al.A numerical study of T-H-M effects on the near-field safety of a hypothetical nuclear waste repository—BMT1 of the DECOVALEX III project.part 3.Effects of T-H-M coupling in sparsely fractured rocks[J].International Journal of Rock Mechanics and Mining Sciences，2005，42(5/6):745－755.