不同地连墙插入深度下承压含水层减压降水对既有隧道的影响
2014-02-13刘庆晨
郑 刚,王 琦,邓 旭,刘庆晨
(1.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300072;2.天津大学 建筑工程学院,天津 300072;3.天津市建筑设计院,天津 300074)
1 引言
天津、上海、杭州、武汉等众多城市均分布不同厚度的承压含水层,若基坑止水帷幕没有完全截断承压含水层,在坑内对承压水层降水的同时,坑外土层中孔隙水压力也将随之下降,引起土体有效应力增加,进而导致地层产生显著的沉降,并且影响范围较广。目前,承压含水层的减压降水已经成为深基坑工程施工中引起坑外地表沉降及邻近建(构)筑物变形的重要原因之一[1]。
昆山某基坑工程,由于止水帷幕未将承压含水层隔断,导致抽降坑内地下水时引起坑外深层地下水和承压水的流失。在基坑内降水至土方开挖前阶段,坑外路面已出现裂缝,且相邻小区房屋的最大沉降量达到25 mm[2]。可见未截断承压含水层情况下,坑内降水对坑外土体及既有结构将产生较大影响,有必要对这一问题进行深入研究。
龚晓南等[3]运用完整井理论提出了反映承压水降压作用的附加分布力公式,进而推导出承压水降压附加分布力作用下的地面沉降公式,并讨论了不同影响因素对沉降的影响;骆冠勇等[4]也提出了下卧承压含水层减压引起的土中应力变化及周围地表沉降的计算方法;叶为民[1]、骆祖江[5]等学者通过建立有限元流固耦合模型,模拟并分析了基坑承压层降水引起地面沉降问题;郑刚等[6]分析了承压水局部降压引起承压水水头下降时,承压含水层及其上覆土层的沉降规律,认为对承压含水层进行局部降压,土体最大沉降值不在地表。但是上述成果主要是针对土体的地表沉降和应力场变化进行研究,对于坑外既有结构,尤其是承压含水层降水对既有盾构隧道结构的影响研究较少。
降水中,止水帷幕对于基坑自身及周边环境的安全具有重要影响。由于承压含水层一般埋藏较深,止水帷幕的深度往往不足以把基坑内外的承压含水层完全截断[2],因此会出现止水帷幕未插入承压含水层、部分插入但承压含水层未被完全截断以及承压含水层被完全截断等不同的情况,而止水帷幕插入承压含水层深度的差异,会对承压水渗流产生不同程度的阻隔作用。本文以此为背景,在隧道位于承压含水层模型的基础上,通过在减压井和既有隧道之间设置地下连续墙作为止水帷幕,研究地下连续墙插入承压含水层深度不同时减压降水对既有隧道变形的影响,并对长期降水及群井降水引起的隧道变形规律也进行了初步研究。
2 有限元模型介绍
2.1 有限元模型建立
采用ABAQUS建立三维有限元流固耦合模型,研究当地下连续墙插入深度不同时,减压降水对既有隧道的影响。既有隧道管片参数以天津地铁2、3号线为依据,管片外径为6.2 m、管片厚度为0.35 m,隧道位于承压含水层中,顶部埋深为22 m,边缘距减压井净距为12.4 m,即2倍隧道外径。为简化分析,避免成层土体分布的影响,在计算模型中承压含水层厚度为12.4 m,顶板埋深为18.8 m,并选取粉质黏土层作为上、下两层隔水层。在模型深度方向取60 m,根据承压水稳定流抽水影响半径经验公式,模型宽度取为400 m,考虑对称性,取1/2模型进行计算,模型几何尺寸如图1所示。
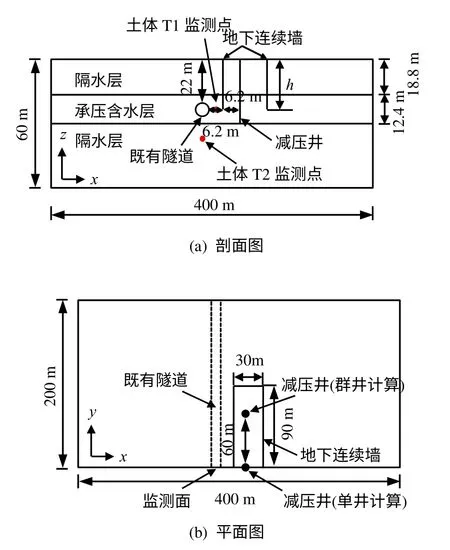
图1 概化土层分布及模型几何尺寸Fig.1 Soil layer distribution&dimensions of model
根据天津地铁车站基坑的一般尺寸,模型中基坑平面尺寸为180 m×30 m,基坑长度方向平行于既有隧道轴线,近隧道侧地下连续墙中心线与既有隧道间距离为6.2 m,位于减压井与隧道的中间位置,地下连续墙墙厚0.8 m。为分析地下连续墙插入深度不同条件下减压降水对既有隧道产生的影响,特设置5种典型深度,其中地下连续墙典型深度h 及与承压含水层的相对位置关系见表1。

表1 地下连续墙与承压含水层位置关系Table 1 Positional relationships between continuous concrete walls and confined aquifer
模型四周边界约束其法向位移,对称面施加对称边界约束,底部约束全部位移。基于土体总孔压变化,采用有效应力法进行流固耦合分析,地下水水位设置在地表,模型底部设置为不排水边界,计算域的侧边界设置常水头进行地下水补给,通过设定降水井出水量模拟承压含水层地下水位下降。
既有隧道与土体之间的切向接触采用库仑摩擦接触面模拟,摩擦系数取为0.3;法向接触采用硬接触,即假设接触面间仅能传递压力而不传递拉力。
2.2 材料参数选择
笔者曾对天津地区某基坑项目的现场降水试验进行过有限元模拟[8],该项目中降水井及观测井的位置如图2所示。根据勘察报告中已有的黏土及粉质黏土层渗透系数,依据所建立的三维模型,对承压含水层单井降水试验中的实际水位变化情况进行模拟,从而估算出各承压含水层土体的渗透系数,并通过群井降水试验进行参数验证(群井降水试验中地下水位拟合曲线如图3所示)。基于已验证的土体水文地质参数,并参照工程地质勘察报告及贾堤等[9]针对天津土层进行的压缩模量 Es与弹性模量E 之间关系的试验研究结果(E≈8Es),在此基础上进行试算调整,拟合实测抽水过程中地表沉降监测点D4的沉降历时曲线(D4点位置见图2),最终确定各土层的模量(部分土层的水文及物理力学参数见表2)。以此得出测点D4沉降历时曲线实测与计算对比如图4所示。
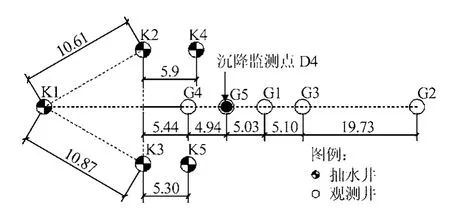
图2 试验井平面图(单位:m)Fig.2 Plan of test well(unit:m)

图3 群井抽水中,观测井观测值与计算值对比曲线Fig.3 Comparison of monitored and calculated water levels during pumping test with multi-well
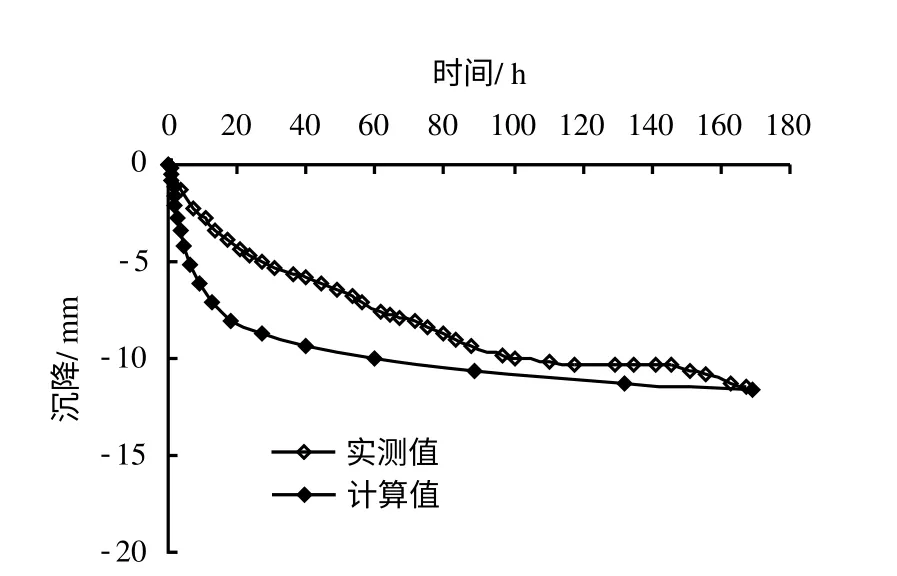
图4 监测点D4沉降历时曲线对比Fig.4 Comparison of curves of settlement versus time of D4
根据上述实际项目的反分析结果,本文模型中选取⑥-1粉土、粉砂层作为承压含水层,而上下隔水层则选取②黏土层,土体采用Mohr-Coulomb弹性-理想塑性模型,相应的水文地质及物理力学参数如表2所示。

表2 土体物理力学参数Table 2 Physico-mechanical parameters of soils
隧道管片混凝土标号为C50,采用错缝拼装,环向和纵向均通过弯螺栓进行连接。本文采用等效刚度法模拟既有隧道,将管片材料本构模型假定为线弹性横观各向同性,通过考虑横、纵向弹性模量不同折减率,用以反映受管片接头、管片环接头影响下,既有隧道横向、纵向刚度不同的特性。根据以往的研究成果,将盾构隧道横向刚度有效率取为75%[10],同时将盾构隧道纵向刚度有效率取为20%[11],管片参数选取见表3。
2.3 承压含水层减压降水模拟
减压井考虑为完整井抽水,井深为31.2 m,抽水量为16 m3/h,通过定义模型中相应位置处结点流量边界的方法进行模拟。

表3 隧道管片力学参数Table 3 Mechanical parameters of tunnel segment
本文分析重点为承压含水层减压降水对既有隧道影响的模拟,因此对隧道开挖的模拟较为简单。隧道采用“Wish-in-place”方法模拟,即认为隧道在模拟初始阶段已经存在。具体的模拟进程如下:
(1)建立初始地应力场,进行地应力平衡。
(2)生成既有隧道,使用稳态分析,即认为周围土体由于开挖产生的超孔压完全消散。
(3)激活承压含水层内抽水流量荷载,使用瞬态分析,模拟减压降水,降水时间为7 d。
3 承压含水层降水对隧道影响的结果分析
本文首先以地下连续墙深度h=18 m,即墙体未插入承压含水层为例,分析减压降水对既有隧道横断面及纵向变形的影响。将对称面位置处的隧道横断面作为监测断面(位置如图1(b)所示),为了便于描述,定义隧道θ=0°处为拱顶,θ=180°处为拱底,θ=90°与θ=270°为拱腰,θ=45°与θ=315°为隧道肩部,θ=135°与θ=225°为隧道趾部,如图5所示。同样,将隧道拱顶、左右拱腰及拱底轴线设为监测线,从而对隧道的纵向变形进行分析。

图5 隧道角度示意图Fig.5 Angles of tunnel
3.1 承压含水层水位降深
图6为减压井抽水过程中,降水井和隧道拱顶处的水位降深随抽水时间的变化曲线。由图可见,在抽水过程中,前10 h减压井内水位迅速下降,而后随着抽水量与含水层内水补给逐渐平衡,水位下降速率不断降低,至40 h,减压井内水位降深达到17 m,趋于稳定。而隧道拱顶水位降深变化趋势与减压井内基本一致,但由于距减压井存在一定距离,导致最终水位降深明显减小。

图6 水位降深随抽水时间的变化曲线(部分数据)Fig.6 Curves of water level versus time(partial data)
3.2 隧道横断面位移及自身变形
图7为隧道监测面在抽水过程中的位移及自身变形示意图。由于减压降水引起的隧道周围土体孔压下降,有效应力上升,导致土体压密,隧道产生沉降,并有整体向减压井方向移动的趋势。随着抽水的进行,隧道竖向位移不断增加,并且拱顶沉降幅度更大,导致隧道竖向直径减小;同时隧道拱腰水平位移也逐渐增大,且右侧拱腰增幅量更大,使隧道水平向直径增加,隧道呈竖向压扁水平伸长状态。隧道水平直径增量略大于竖向直径减小量,降水过程中各位置相应位移值如表4所示。
3.3 隧道纵向变形分析
承压含水层减压抽水,必然导致该层土体固结压密,进而引起相邻土层位移场随之发生变化。图8为模型中承压含水层抽水58 h后,沿隧道轴向方向土体的竖向位移场分布,以隆起为正、沉降为负。
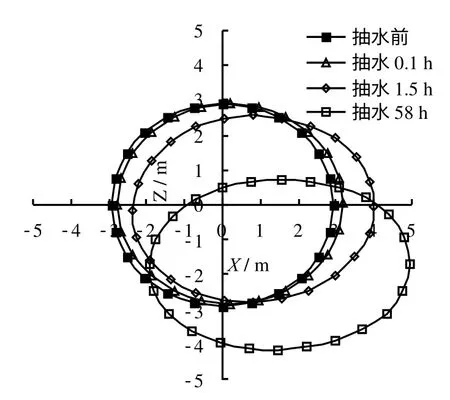
图7 抽水过程中隧道位移(放大500倍)Fig.7 Displacements of tunnel during pumping process(magnified 500 times)

表4 抽水过程中隧道各点位移值Table 4 Displacements of tunnel points during pumping process

图8 土体竖向位移场分布(单位:m)Fig.8 Displacement field of soil(unit:m)
从图中可以看出,当抽水58 h后,受减压井在含水层抽水的影响,承压含水层产生固结沉降,沉降值由下而上依次累加,在该层顶部达到最大;上部隔水层由于下方含水层沉降及向下的渗流作用,同样产生沉降变形,但是表现为靠近承压含水层土体沉降大,向地表方向沉降逐渐减小,土体呈拉伸状态;同时,下部隔水层在向上的渗流作用下发生回弹,尤其在靠近对称面附近区域回弹现象较明显,但位移值相对较小,随着深度的增大,回弹量逐渐减小,土体同样表现为拉伸状态。
图9为抽水58 h后,既有隧道各纵向监测线位移分布。规定竖向位移增量,正值为隆起,负值为沉降;而水平向位移增量,正值为向抽水井方向移动,负值为远离抽水井方向移动。从图中可以看出:
(1)当水位稳定后,各测线通长均产生一定的位移。拱顶、拱底测线均为沉降状态,拱腰测线则向减压井方向的偏移,且除拱底监测线外,其余曲线的最大位移均出现在对称面,即减压井位置处。各曲线基本表现为随着距减压井距离的增加,位移量逐渐减小,两相对测线间的相对位移(直径增量)也逐渐减小,此时隧道的竖向位移略大于水平位移。
(2)承压含水层减压降水的影响范围非常远,据计算可知,距减压井150 m外,仍有近1 m的水位降深,而根据前文的分析,当隧道处水位发生下降,既有隧道就会受其影响引起变形,因此从图中可以看出,距减压井外150 m处的隧道拱顶仍存在1 mm左右沉降。
(3)当抽水时长较短(58 h)时,对于拱底监测线,其沉降并非完全随着距对称面距离增加逐渐减小的凹槽形,而是表现为“W”形分布,最大沉降位置位于距对称面30 m附近。结合图6所示土体竖向位移场可以推测,产生这种现象的原因主要是由于减压井降水引起下部隔水层在靠近对称面附近区域产生回弹,从而制约了隧道拱底沉降。在实际工程中,隧道弯曲过大可以造成管片环间接缝张开,甚至发生漏水、漏砂事故,需要引起关注。
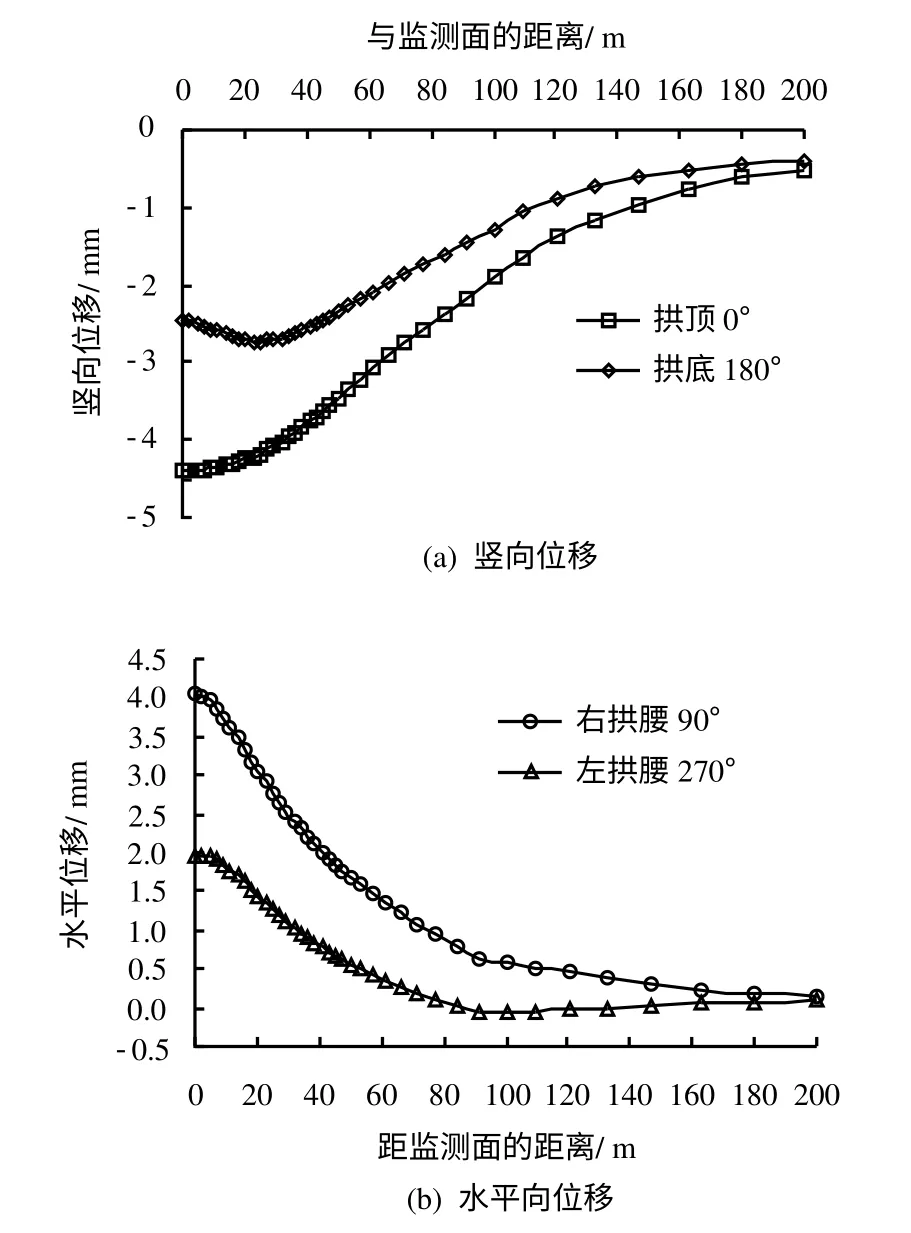
图9 既有隧道各纵向监测线位移分布Fig.9 Displacements of monitoring lines of exsiting tunnel
4 地下连续墙不同插入深度条件下减压降水对隧道变形的影响
在前文的分析基础之上,本文将进一步研究当地下连续墙插入承压含水层深度不同时,减压降水对既有隧道变形的影响。前文算例中的结论,均为减压井处水位降深17 m条件下的计算结果,为便于进一步比较分析,本节中地下连续墙插入承压含水层不同深度条件下的隧道变形也均取自基坑内的减压井处水位降深为17 m时的计算结果。
4.1 不同插入深度条件下隧道处水位降深比较
图10为地下连续墙插入承压含水层不同深度情况下,既有隧道监测面处拱顶水位降深随减压井水位降深的变化。由于地下连续墙对地下水渗流的阻碍作用,当减压井水位降深相同时,随着地下连续墙插入承压含水层深度的增加,坑内外水力联系减弱,减压降水引起的既有隧道拱顶处水位降深逐渐减小,当承压层被完全截断时,隧道拱顶处水位几乎不变。
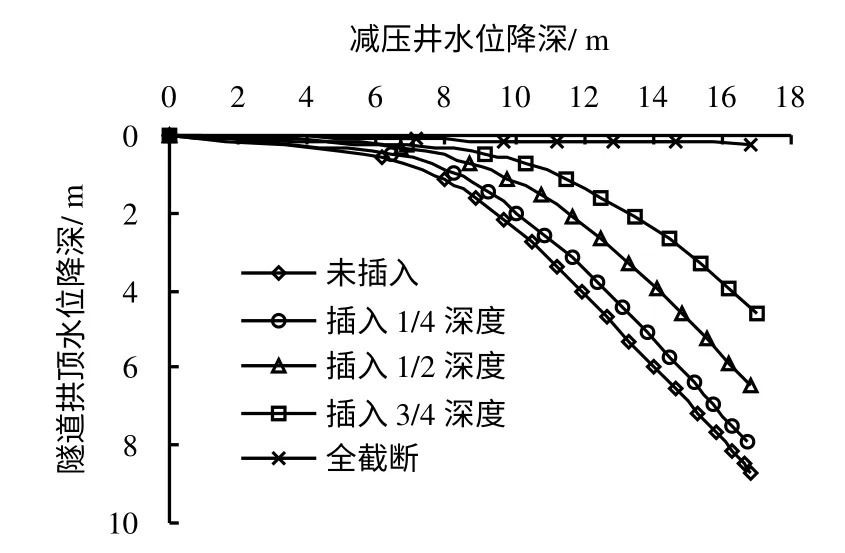
图10 不同插入深度条件下监测面处隧道拱顶水位降深随减压井水位降深的变化Fig.10 Water level at tunnel vault of monitoring surface versus water level of well with different inserted lengths of diaphragm wall
4.2 不同插入深度条件下隧道横断面变形比较
图11为当减压井水位降深17 m时,不同插入深度条件下,减压降水引起的隧道监测面位移及自身变形示意图,表5为各位置的相应位移值。
随着地下连续墙插入承压含水层深度的增加,相同条件下减压降水引起的隧道处水位降深减小,导致隧道拱顶拱底的沉降逐渐减小。当承压层被完全截断时,隧道拱顶仅产生0.53 mm的沉降,同时拱底由沉降逐渐变为上抬变形。但值得注意的是,隧道的水平位移随截断条件变化却不大,对于θ=90°拱腰处,当承压含水层未被完全截断时水平位移约为4 mm,而完全截断条件下仍存在3.3 mm的位移。同样,当地下连续墙未完全截断承压含水层时,隧道的竖向和水平直径增量变化也较小,变化范围在0.024%D~0.034%D(D为隧道直径)之间,仅当承压含水层被完全截断时才产生明显的减小,约为0.013%D。

图11 不同插入深度条件下隧道位移(放大500倍)Fig.11 Displacements of tunnel with different inserted lengths(magnified 500 times)

表5 不同插入深度条件下隧道各点位移值(单位:mm)Table 5 Displacements of tunnel points with different inserted lengths
4.3 不同插入深度条件下隧道纵向变形比较
图12为当减压井水位降深17 m时,地下连续墙插入承压含水层不同深度条件下,既有隧道各纵向监测线的分布。由图可知:
(1)随着地下连续墙插入承压含水层深度的增加,既有隧道沉降逐渐减小,最大沉降值由4.4 mm减小为0.53 mm,同时隧道的纵向弯曲程度也明显减弱。当承压含水层全截断时,监测面附近处的隧道变形转变为拱顶沉降、拱底上抬变形。
(2)既有隧道右拱腰测线在承压含水层未被完全截断时,近监测面处隧道的水平位移几乎相同,约为4 mm,并未随拱顶水位降深减小而减小,且当承压含水层被完全截断时,隧道右拱腰处最大位移仍为3.3 mm。隧道左拱腰测线水平位移随承压含水层截断程度的提高而增加,但增幅较小,当地连墙未插入承压含水层时,左拱腰的最大水平位移为2.0 mm,而当承压含水层被完全截断时最大位移约为2.4 mm。

图12 不同插入深度条件下既有隧道各纵向监测线位移分布Fig.12 Displacements of monitoring lines of exsitng tunnel with different inserted lengths
图13为对称面处地下连续墙最大水平位移、土体T1监测点(位置如图1(a)所示)以及隧道拱腰90°在地连墙不同插入深度条件下的水平位移对比曲线。由图可以看出,当既有隧道与地下连续墙距离为1倍隧道直径时,地下连续墙插入承压含水层的深度对隧道水平位移影响较小,即使完全截断承压水的渗流路径,基坑内的减压降水仍然会引起地连墙产生向坑内的方向的位移,进而造成坑外土体及隧道也相应发生水平变形。说明当既有隧道与减压井净距较小时,即使承压含水层被完全截断,仍应重视坑内减压降水对隧道水平方向变形造成的影响。
(3)承压含水层截断与否对隧道直径的增量变化也将产生影响。当承压含水层未被完全截断时,随着地下连续墙插入承压含水层深度的增加,隧道竖向及水平直径增量均逐渐减小,但变化幅度相对较小。而在承压含水层被完全截断情况下,直径增量变化比较明显,最大增量约为0.033%D(0.9 mm)。此时隧道轴向的变形范围最远距监测面约90 m,即为地下连续墙的长度范围。说明当承压含水层被完全截断时,减压降水对坑外既有隧道的影响范围基本在地下连续墙长度范围以内,主要由地下连续墙的变形引起。
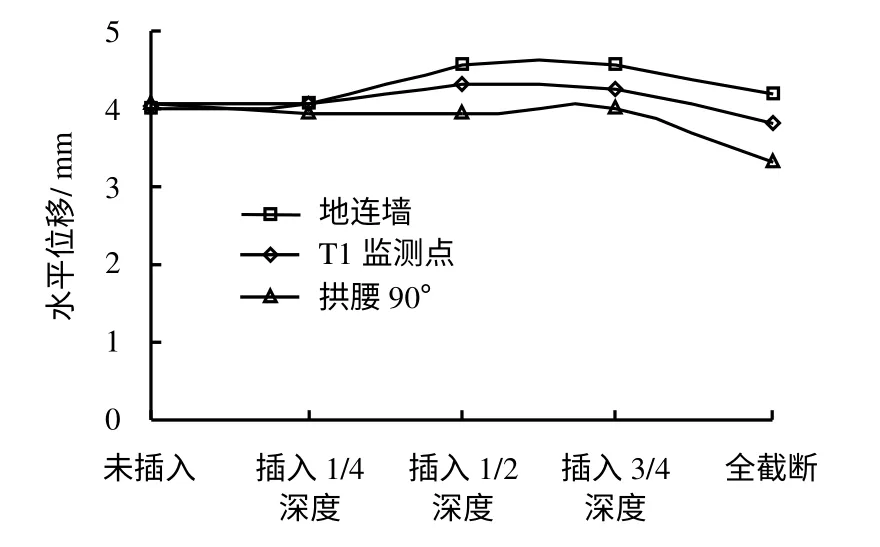
图13 不同插入深度条件下各监测点水平位移变化Fig.13 Horizontal displacements of monitoring points with different inserted lengths
5 承压含水层长期降水对隧道影响的结果分析
前文分析了在承压含水层短期减压降水(58 h)条件下,基坑外既有盾构隧道的变形情况。但是基坑施工并非短期问题,在某些情况下要保证减压井长时间抽水,这势必会对既有隧道产生更加剧烈的影响。因此,在前文的计算结果基础上,将进一步研究长期减压降水条件下基坑外既有隧道的位移及自身变形情况。
5.1 单井情况下长期降水的影响
本文第3节已经详细探讨了地连墙在未插入承压含水层条件下,减压降水58 h引起的坑外既有隧道变形规律,本节将在此模型基础上进一步研究降水2 400 h(100 d)条件下,既有隧道的变形情况。
5.1.1 隧道横断面位移及自身变形
从图6可以看出,减压降水40 h后,减压井内水位降深达到17 m,隧道拱顶水位降深约9 m,均趋于稳定,因此降水2 400 h后,水位降深基本保持不变。
图14为隧道监测面在抽水58 h及2 400 h后的位移及自身变形示意图,相应各位置的位移值如表6所示。

图14 抽水过程中隧道位移(放大150倍)Fig.14 Displacements of tunnel during pumping process(magnified 500 times)

表6 抽水过程中隧道各点位移值Table 6 Displacements of measuring points of tunnel during pumping process
结合图4、图14及表6可以发现,当抽水58 h后,隧道顶部的水位降深已趋于稳定,此时隧道最大产生4.4 mm沉降及约2 mm的竖向压缩变形;而经过2 400 h抽水后,隧道沉降明显增加,拱顶最大沉降达到18.6 mm,但隧道的竖向压缩变形却有所减小,仅为1 mm左右。为解释出现这种现象的原因,在隧道下方的隔水层中设置一土体位移监测点T2(位置如图1(a)所示),绘制该点的水平及竖向位移时程曲线见图15。可以发现,隧道下隔水层中的土体水平位移是随着时间增加逐渐增长且趋于稳定,但其竖向却并非是随着抽水时间增加逐渐沉降的。当抽水时间小于40 h,由于向上的渗流作用,隧道下部隔水层产生一定的回弹;此后随着抽水时间继续增加,隔水层内土体排水固结,逐渐转为沉降。因此,对上部承压含水层中隧道而言,当下卧土体回弹时,竖向压力增加,隧道产生竖向压缩变形;而当下部土体开始排水固结沉降后,虽然隧道也随之产生整体的下沉,但是由于隧道底部所受的的竖向压力减小,竖向压缩变形有所缓解,因此,产生竖向直径增量减小的现象。
5.1.2 隧道纵向变形分析
图16为模型中承压含水层抽水2 400 h后,沿隧道轴向方向土体的竖向位移场分布,以隆起为正、沉降为负。与抽水58 h后土体竖向位移场(见图6)相比,当抽水时长2 400 h,土层则均表现为沉降,且自上部而下部沉降值逐渐减小。
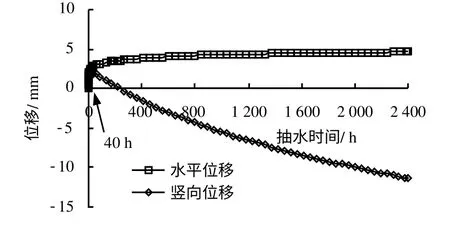
图15 T2监测点位移历时曲线Fig.15 Curves of displacement versus time of T2

图16 土体竖向位移场分布(单位:m)Fig.16 Vertical displacement field of soil(unit:m)
图17为抽水58 h与2 400 h后,既有隧道各纵向监测线位移分布,其中隧道位移方向的正负值与前文相同,不再赘述。通过对比可以看出,受土体长期固结沉降的影响,隧道产生较大的沉降,最大沉降值达18.6 mm,并且与短期降水相比,隧道竖向弯曲更加剧烈。但与之相比,隧道在水平方向的位移,仅比短期降水增加了2.5 mm。因此,承压含水层内减压降水对含水层内既有隧道的影响更主要是表现在沉降方面,需要加强对隧道竖向变形的控制与保护。
5.2 群井情况下长期降水的影响
基坑工程中承压含水层减压降水通常都是进行群井降水,其对土体及既有结构产生的影响也必定与单井降水有所差异。在前文单井降水的基础上,本文也对群井降水进行了简单的研究。群井降水的模型与上文单井长期降水模型相同,仅在基坑内部增加一口相同的降水井,增加的降水井位置如图1(b)所示。
群井降水2 400 h后,既有隧道各纵向监测线的位移分布曲线也绘制在图17中。通过与单井长期降水(2 400 h)的位移曲线对比可以看出,群井降水情况下,引起的隧道沉降更加剧烈,并且隧道的凹槽形沉降范围也更宽,隧道弯曲亦明显增加。相比而言,隧道水平方向的位移值增加并不多,但是受到群井降水的影响,隧道的水平向呈波浪形弯曲,这种变形容易造成隧道环缝张开及管片开裂,对隧道的安全极其不利。
通过前文对承压含水层长期降水条件下既有隧道变形的对比分析可知,当承压含水层未被完全截断时,长期进行承压含水层减压降水将会引起下部隔水层土体的排水固结,进而引起隧道产生严重的沉降及弯曲变形,尤其是在群井降水情况下,变形更加剧烈,隧道水平方向还会产生波浪形弯曲。在实际工程中,应避免在承压含水层未被完全截断情况下进行减压降水,若需要长期减压降水,必须隔断靠近隧道一侧的承压含水层。

图17 既有隧道各纵向监测线位移分布Fig.17 Displacements of monitoring lines of existing tunnel
6 结论
采用ABAQUS软件建立有限元模型,研究承压含水层减压降水对邻近既有隧道横断面及纵向变形的影响,在此基础上,针对地下连续墙插入承压含水层深度、长期降水和群井降水进行参数分析,得到如下结论:
(1)短期降水情况下,承压含水层减压降水将引起含水层中隧道沉降,并产生竖向压缩水平伸长变形。减压降水同样也会导致隧道发生纵向弯曲,并且受到下部隔水层回弹变形的制约作用影响,隧道拱底监测线的沉降变形呈“W”形分布。
(2)随着地下连续墙插入承压含水层深度的增加,坑内减压降水对坑外水位的影响逐渐减小,当承压含水层被完全截断条件下,坑外水位几乎不变,进而导致隧道的竖向位移、直径增量及纵向弯曲变化也均有明显的减小。因此,若基坑外存在既有隧道,进行坑内减压降水,建议应截断隧道一侧的承压含水层。
(3)若既有隧道与地下连续墙之间距离较近(如1倍隧道直径)时,随着地下连续墙插入承压含水层深度的增加,虽然既有隧道沉降及纵向弯曲程度均减小,但是承压含水层截断与否对隧道水平位移影响却很小,即使截断承压水的渗流路径,减压降水产生的水平位移变化仍会由地下连续墙变形对周围土体的扰动作用而将影响传递。因此,当既有隧道与减压井净距较小时,即使承压含水层被完全截断,仍应重视坑内减压降水对隧道水平方向变形造成的影响。
(4)当承压含水层被完全截断时,减压降水对坑外既有隧道的影响范围主要集中在地下连续墙长度范围以内,隧道变形主要由地下连续墙的变形引起,该范围以外隧道几乎不产生纵向变形和直径增量变化。
(5)在承压含水层未被完全截断条件下,长期减压降水将会造成下部隔水层土体排水固结,引起隧道产生可观的沉降,尤其是在群井降水情况下,隧道在水平方向还会产生波浪形弯曲变形。因此,应避免在承压含水层未被完全截断情况下进行减压降水,若需要长期减压降水,必须隔断靠近隧道一侧的承压含水层。
本文以简单的土层条件为基础,对承压含水层减压降水引起的既有隧道变形机制和规律进行了探讨,并在此基础上初步分析了地连墙插入深度、长期降水以及群井降水产生的影响。今后会继续结合实际工程和真实的地质条件进行深入研究,进一步验证及完善本文总结的机制和规律。
[1]叶为民,万敏,陈宝,等.深基坑承压含水层降水对地面沉降的影响[J].地下空间与工程学报,2009,5(增刊2):1799-1805.YE Wei-min,WAN Min,CHEN Bao,et al.Influence of dewatering of confined aquifers on land subsidence during deep excavation[J].Chinese Journal of Under-ground Space and Engineering,2009,5(Supp.2):1799-1805.
[2]陈永才,李镜培,邸国恩,等.某深基坑降水对周边环境影响的分析及处理措施[J].岩土工程学报,2008,30(增刊1):319-322.CHEN Yong-cai,LI Jing-pei,DI Guo-en,et al.Analysis and repair measures for influence of dewatering of deep foundation pits on surrounding environment[J].Chinese Journal of Geotechnical Engineering,2008,30(Supp.1):319-322.
[3]龚晓南,张杰.承压水降压引起的上覆土层沉降分析[J].岩土工程学报,2011,33(1):145-149.GONG Xiao-nan,ZHANG Jie.Settlement of overlaying soil caused by decompression of confined water[J].Chinese Journal of Geotechnical Engineering,2011,33(1):145-149.
[4]骆冠勇,潘泓,曹洪,等.承压水减压引起的沉降分析[J].岩土力学,2004,25(增刊2):196-200.LUO Guan-yong,PAN Hong,CAO Hong,et al.Analysis of settlements caused by decompression of confined water[J].Rock and Soil Mechanics,2004,25(Supp.2):196-200.
[5]骆祖江,刘金宝,李朗.第四纪松散沉积层地下水疏降与地面沉降三维全耦合数值模拟[J].岩土工程学报,2008,30(2):193-198.LUO Zu-jiang,LIU Jin-bao,LI Lang.Three-dimensional full coupling numerical simulation of groundwater dewatering and land-subsidence in quaternary loose sediments[J].Chinese Journal of Geotechnical Engineering,2008,30(2):193-198.
[6]郑刚,曾超峰,薛秀丽.承压含水层局部降压引起土体沉降机制及参数分析[J].岩土工程学报,2014,36(5):802-817.ZHENG Gang,ZENG Chao-feng,XUE Xiu-li.Mechanism of settlement induced by local pressure-relief of confined aquifer and parameter analysis[J].Chinese Journal of Geotechnical Engineering,2014,36(5):802-817.
[7]姚天强,石振华.基坑降水手册[M].北京:中国建筑工业出版社,2006.
[8]郑刚,邓旭,刘庆晨.承压含水层减压降水对既有盾构隧道的影响[J].岩土力学,2015,36(1):待发表.ZHENG Gang,DENG Xu,LIU Qing-chen.Analysis of responses of the existing shield tunnel due to pressure-relief of confined aquifer[J].Rock and Soil Mechanics,2015,36(1):(to be published).
[9]贾堤,石峰,郑刚,等.深基坑工程数值模拟土体弹性模量取值的探讨[J].岩土工程学报,2008,30(增刊1):155-158.JIA Di,SHI Feng,ZHENG Gang,et al.Elastic modulus of soil used in numerical simulation of deep foundation pits[J].Chinese Journal of Geotechnical Engineering,2008,30(Supp.1):155-158.
[10]LEE K M,GE X.W.The equivalence of a jointed shield driven tunnel lining to a continuous ring structure[J].Journal of Canadian Geotechnical Engineering,2001,38:461-483.
[11]钟小春,张金荣,秦建设,等.盾构隧道纵向等效弯曲刚度的简化计算模型及影响因素分析[J].岩土力学,2011,32(1):132-136.ZHONG Xiao-chun,ZHANG Jin-rong,QIN Jian-she,et al.Simplified calculation model for longitudinal equivalent bending stiffness of shield tunnel and its influence factors’ analysis[J].Rock and Soil Mechanics,2011,32(1):132-136.
