利用倒频谱辨别薄层的联合反演算法*
2014-02-13黄忠来
吴 楠 黄忠来
1)贵州师范大学机械与电气工程学院,贵阳 550001
2)厦门大学信息科学与技术学院,厦门361005
1 引言
层状介质是探地雷达实际应用中经常遇到的介质分布类型,当地下目标层为相对厚层时,层的顶、底反射波可以在时域被区分,因此这类目标层的厚度、深度以及电性参数可利用反射面反射波的振幅进行估算[1,2]。但是,当地下存在厚度小于调谐厚度的薄层时,顶、底反射波会在时域混叠在一起。这时,利用时域反演方法得到的结果将不再准确。因此,频率域反演方法被引入处理地下含有薄层的情况。频率域反演方法需要建立地下介质模型,构造目标函数,并利用线性或非线性反演方法进行迭代计算[3,4]。当地下目标层的个数较多时,如果要同时反演目标层的几何与电性参数,则需要反演的参数数量众多,导致计算效率低下,且反演的结果容易收敛在局部极小值。通过采用接近真实值的迭代初值,或减少反演迭代的参数个数,都可以加快反演算法的收敛速度,提高反演结果的准确度。在实际资料处理过程中,先验信息的获取有时非常困难。虽然文献[5-8]提出的多步骤的谱反演算法,可以提高反演的效率和准确度。但是,算法中需要对地下反射面的分布有初步的划分,而薄层识别则是难点。
为解决这一问题,本文结合谱反演算法,提出了一种利用倒频谱技术的频率域联合反演算法。
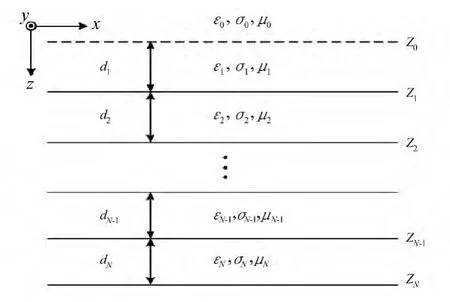
图1 地下包含N 个反射面的层状介质模型Fig.1 A layered media model containing N underground layers
2 算法原理
2.1 模型及目标函数
对于图1 中所示的水平层状模型,设地下第i个反射面的反射系数为ri,若不考虑各反射面之间的多次波,则该反射面反射波的幅度Ai可以表示为[7]
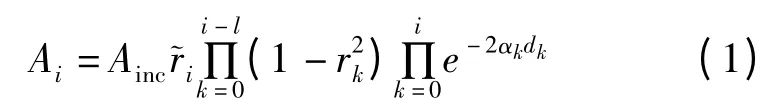
其中Ainc是探地雷达入射波幅度为反射面的广义反射系数,αk是电磁波在地下第k 层介质中传播时的衰减常数,dk是电磁波在第k 层介质中的单向传播距离。地表接收到的雷达回波s(t)可以表示成雷达子波和反射系数序列的褶积,
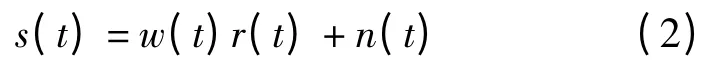
其中w(t)为雷达发射波,r(t)为地下介质反射系数序列,n(t)为加性噪声。若地下有N 个反射面,将反射系数序列中每相邻两个反射系数组成一个反射系数对,并对其做奇偶分解,如图2 所示。因此反演算法的目标函数可以写为[7]:

由于反射面上的广义反射系数是电性参数的函数,所以在反演时反射系数的奇偶分量可以用含有电性参数的表达式替换,这样不仅可以反演出目标层的物理属性,还可以反演出所含介质的电性参数。
2.2 基于倒频谱的薄层识别

考虑地下只含有两个反射系数,且目标层为薄层情况。设上反射面的广义反射系数为,下反射面的为;上反射面距离地表的时间距离为t1,下反射面的为t2。由于发射波的能量有限,且有噪声存在,所以需要用窗口限制分析的带宽。带限的反射系数序列频谱可以表示为:
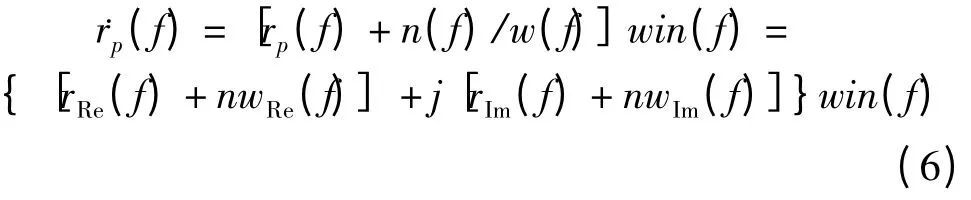
其中rp(f)为反射系数序列频谱,rRe(f)和rIm(f)分别是rp(f)的实部和虚部。注意到实部和虚部的相位相差π/2,且倒频率相同项的符号相反,幅值相同。win(f)为窗函数,nwRe(f)和nwIm(f)分别是n(f)/w(f)项的实部和虚部。将的实部和虚部分别表示为和,即
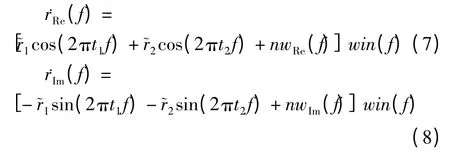
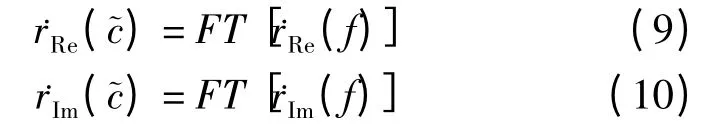
序列频谱的实部和虚部都是频率域函数,它们包含相同的倒频率成分,此时倒频率即是反射系数的时间位置参数t1和t2,因此,在实部和虚部倒频谱的t1和t2位置处会出现两个钟形尖峰。对于薄层来说,两个钟形尖峰会重合在一起,尖峰所对应的倒频率值tp满足t1≤tp≤t2。由于反射系数频谱实部和频谱虚部对应倒频率成份的符号相反,相位相差π/2,因此如果移动虚部(实部)的某一倒频率成分的相位,使之和实部(虚部)的相应倒频率成分相位一致,那么两者相加后,这一倒频率能量必然会消失。如果原先的频谱实(虚)部中只存在一种倒频率成分,那么两者之和的频谱中必然没有能量峰值;如果原先频谱实(虚)部中存在两种倒频率成分,那么两者之和的频谱中会有能量残留。因此,根据能量是否残留,就可以判断倒频率成分的数量,即反射面的个数。
在改变频谱实(虚)部中某一倒频谱成分的相位时,还需要考虑分析频带带宽的影响。例如,我们的目的是改变反射系数频谱虚部包含倒频率t1项的相位,即将虚部中的sin(2πt1f)项转化为实部中的cos(2πt1f)项。所以将反射系数序列频谱虚部的频谱乘以,再将结果进行逆傅立叶变换,这里,相位因子τ=(4n +1)/4t1。为了避免在分析频谱中引入较大噪声,我们在限制分析频带后再进行相位移动。分别利用窗口函数win(f)和winτ(f)= win(f-τ)对反射系数序列频谱进行截取。利用winτ(f)进行分析频带限制的反射系数序列频谱记为,
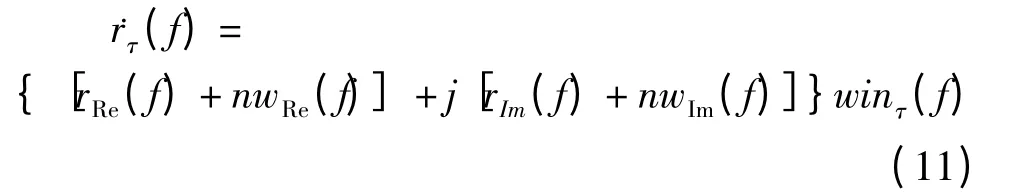
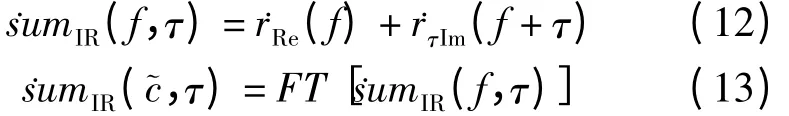
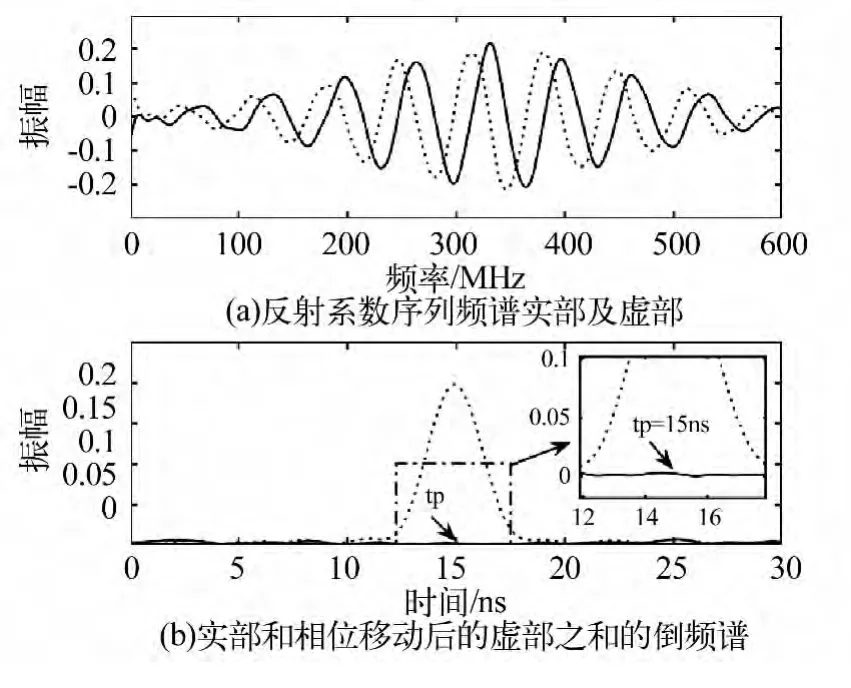
图3 目标为单反射面时的结果Fig.3 result of the target as a reflection interface
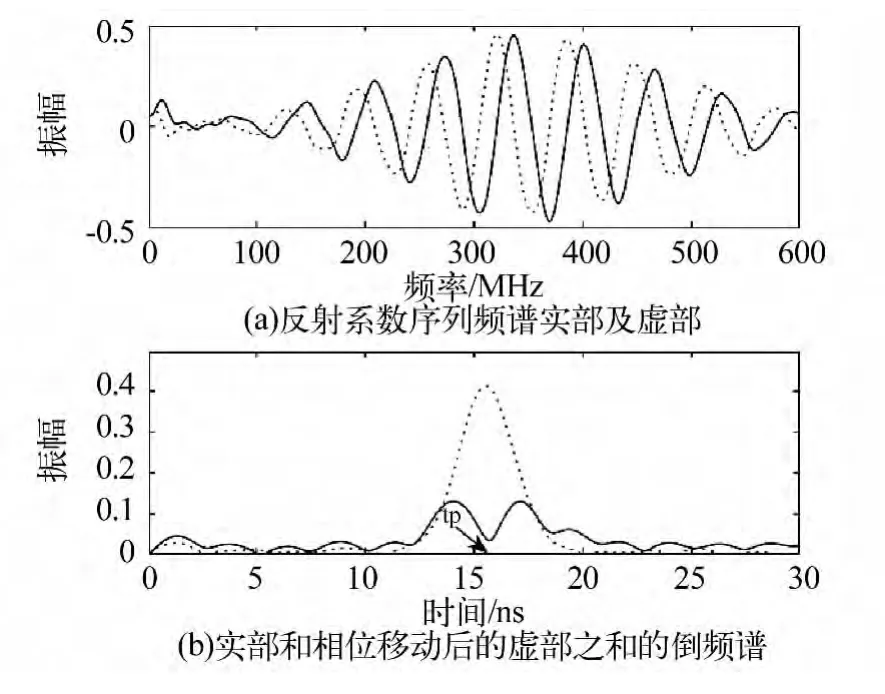
图4 目标为薄层时的结果Fig.4 result of the targ thin layer
3 实际资料处理
实际GPR 数据来自公路检测资料,公路表面为沥青,且沥青面层分为3 层,厚度分别是0.04 m,0.06 m 和0.1 m。在沥青面层之下还铺了一层防水层。如图5(a)所示,在8 ns 处的即为防水层。天线发射频率为2 GHz,每道采集1 024 个数据,采集10 ns。我们以第15 道数据为例,来检验算法的处理效果,数据的时域波形如图5(b)所示。其实部倒频谱如图5(c)中虚线所示,可以看到,实部倒频谱中出现了4 个峰值,其中第一个代表地表;第二个代表沥青面上层和中间层的分界面反射波,峰值倒频率为tp1;第三个代表中间层和下面层分界面的反射波,峰值倒频率为tp2(图5(d));而最后一个峰值则代表防水层,峰值倒频率为tp3(图5(e))。
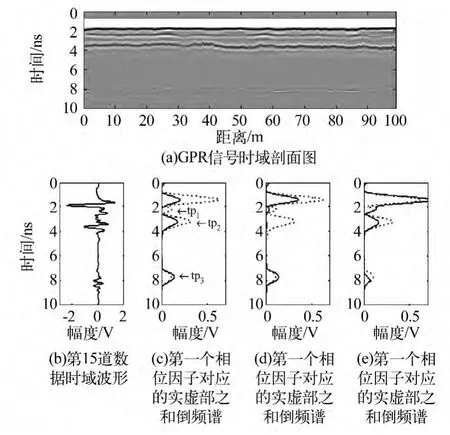
图5 探地雷达资料剖面图及波形图Fig.5 GPR data profile and waveform of the data
三个峰值倒频率可以得到三个不同的相位因子,τ1、τ2和τ3,根据这三个因子对反射系数频谱虚部进行相位移动,分别得到和。计算它们的频谱,结果如图5(b)、(c)、(d)中的实线所示。从图5(b)和(c)可以看到,由于这两个峰值所指示的都是单一反射面,所以tp1 和tp2 处的能量在进行相加后都消失了。而tp3 处是一个薄层,所以在和的频谱中有明显能量残留。根据倒频谱结果,我们用三个窗口划分数据,并对每个窗口数据进行反演,反演采用随机爬山算法。第一个窗口包含了地表回波和第一个反射面的回波。第二个窗口只包含第二个反射面的回波,第三个窗口包含薄层。图6(a)和(b)分别是数据的时域剖面图和反射面的反演结果。薄层的平均反演厚度为0.01m,大约为波长的1/5。从上倒下各层的介电常数分别为3.7、5.4、12、9.3 和13.2。电导率分别是0.013、0.02、0.018 和0.01。
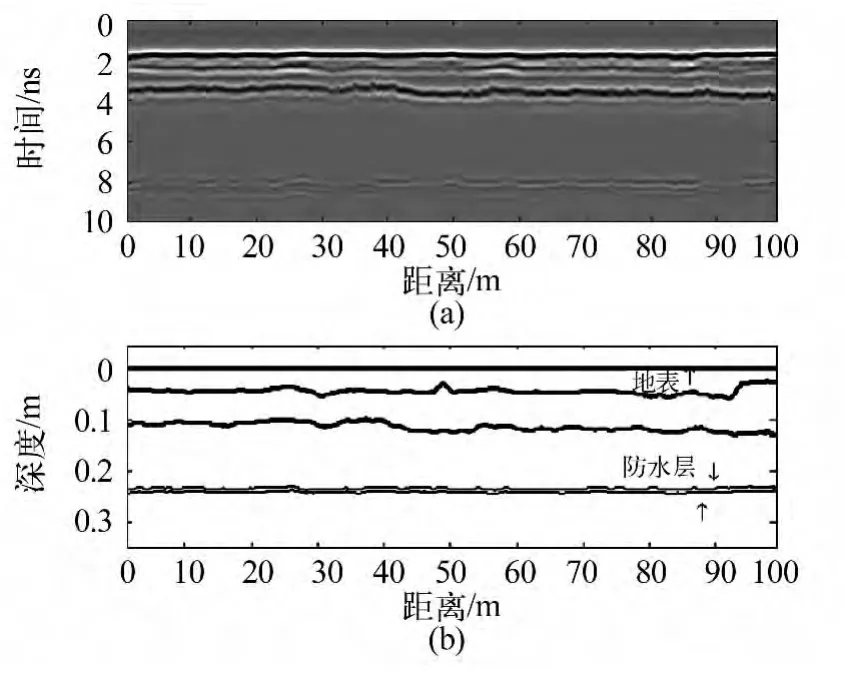
图6 时域剖面图(a)和层面反演结果(b)Fig.6 GPR data profile(a)and inversion result of the layer interfaces(b)
4 结语
由于倒频谱上的峰值指示了地下反射面的位置,因此,利用两者对薄层进行辨识,以解决谱反演算法中的层面识别问题。首先,将反射系数序列频谱的虚部进行相位移动,将结果与未进行相位移动的频谱实部进行相加,随后计算两者之和的倒频谱,通过观察倒频谱上峰值能量的变化,可以判断峰值指示的是单反射面还是薄层。若和的倒频谱在峰值处能量消失,则该处为单反射面;若峰值处能量有较大残留,则该处为薄层。该方法可以为谱反演方法提供层面位置和数量的先验信息,从而提高反演算法的计算效率和结果准确度。
1 AL-Qadi I L and Lahouar S.Measuring layer thicknesses with GPR-theory to practice[J].Construction and Building Materials,2005,19:763-772.
2 Kao Chienping,et al.Measurement of layer thickness and permittivity using a new multilayer model from GPR data[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(8):2 463-2 470.
3 Qin Yao,et al.Research on thin-layer recognition technique based on the spectrum inversion method of ground penetrating radar[J].Journal of Electronics and Information Technology,2010,32(11):2 760-2 763.
4 Julien M,et al.A generalized frequency domain reflectometry modeling technique for soil electrical properties determination[J].Vadose Zone Journal,2010,9(4):1 063-1 072.
5 Puryear C I and Castagna J P.Layer-thickness determination and stratigraphic interpretation using spectral inversion:Theory and application[J].Geophysics,2008,73(2):37-48.
6 黄忠来,张建中.探地雷达薄层信号的谱反演算法[J].大地测量与地球动力学,2011,(4):154-159.(Huang Zhonglai and Zhang Jianzhong.A spectral inversion algorithm for GPR signals of thin layers[J].Journal of Geodesy and Geodynamics,2011,(4):154-159)
7 黄忠来,张建中.利用探地雷达频谱反演层状介质几何与电性参数[J].地球物理学报,2013,56(4):1 381-1 391.(Huang Zhonglai and Zhang Jianzhong.An inversion method for inverting geometric and electric parameters of layered media using spectrum of GPR signal[J].Chinese Journal of Geophysics,2013,56(4):1 381-1 391.
8 Giannopoulos A.Modeling ground penetrating radar by GprMax[J].Construction and Building Materials,2005,19:755-762.
