含零元的同余自由正则半群的一个注记

罗肖强

（四川文理学院数学与财经学院，四川达州 635000）

含零元的同余自由正则半群的一个注记

罗肖强

（四川文理学院数学与财经学院，四川达州 635000）

设S是一正则半群为正则半群S上的幂等元集。通过建立S上的几种集合关系，得到了判断含零元同余自由正则半群的新方法。

正则半群;幂等元集;析取集;同余自由正则半群

在文献〔1〕中J.M.Howie给出了同余自由半群的概念：设半群S有一真理想I，Rees商是S的一真同态象。若S上只有1S（相等关系）和S×S（全关系），且S是单的或零单的，则S是同余自由半群。若半群S是有限的，S一定是完全单的或完全零单的。至于在无限半群里的情况，Munn（1972-1974）做了这方面的论述。现在问题的关键是半群S含有零元与不含零元是否也构成同余自由半群，对于这个问题Howei通过矩阵半群已经做了很好的研究。一些构造特殊的同余自由半群的研究情况怎样呢?Munn在文献〔2〕和Trotter在文献〔3〕中得到了S是同余自由逆半群的充要条件S是单的或者零单的基本逆半群;Bailes在文献〔4〕中证明了同余自由纯整半群既是同余自由逆半群，也是阶为2的左（或右）零半群；华南师范大学的汪立民教授在文献〔5〕中研究了带有Q逆变换的同余自由正则半群。鉴于以上研究，在本文里，设E()S为正则半群S上的幂等元集，在E()S中建立如下关系：，得到了E(S)是析取的，从而获得了判断同余自由正则半群的新方法。

1 准备

引理1设E(S)是正则半群S的幂等元集，则对任意，存在使得

证明：（2）半序关系显然，只证后一结论。设任意，则h∈E(S)。由h∈E(S)知he=h。同样由≤Rf得到 fh=h，而h=he=fhe∈fSe，于是

反之，设任意 h∈fSe∩E(S )，则h∈E(S )，若，则有等式，从而h∈M(e ,f)。于是。

引理2设ρ是正则半群S上的同余，eρf,e,f∈E(S)则

证明：（1）由于,则efρe,又因为g∈S(e ,f)，所以 g=geρgf，从而得到故

引理3 设ρ是正则半群S上的同余，对于任意e,f∈E(S)，

证明：（1）若(eρ) R( fρ)，则有。又因为，因此有，而则gρe。

（2）与（1）的证法类似。

引理4 设ρ是正则半群S上的同余，且ρ不是幂等元分离同余，则S一定存在幂等元e,f，使得eρf,e≤f,eRf,eLf。

证明见参考文献〔7〕。由此我们可得如下推论。

推论5 设正则半群S含有零元。若 peq=0, pfq≠0,对任意e,f,p,q∈E(S)，h∈S(p,f),k∈S(f,q)，则 S(h,fk) ek=0，heS(hf,k)=0，0∉S(h,fk) fk， 0∉hfS(hf,k)。

为了后面行文方便，这里我们做如下的记法，任意e,f∈E(S)，若记为e≤f。若e≤f，且，记为eΩf。

引理6 若幂等元集E(S)是析取的，E(S)必须满足对任意e,f∈E()S，e≠f使得eΩf，eRf,eLf，存在0≠g∈E()S，其中有

（1）若eΩf，则 fg=g,geg=0;

（2）若eRf，则gf=g,geg=0;

（3）若eLf，则 fg=g，geg=0。

证明：见参考文献〔8〕。

2 结论

定理7 设正则半群S含有零元，ρ是S上的同余，那么幂等元集E(S)是析取的充要条件是且 ρ是幂等元分离同余。

证明:首先注意，对于任意c,d∈S1，有ced=0, e∈E(S)有的逆元反之亦成立。因此 ρ是幂等元分离同余的充要条件是对于任意存在 p,q∈E(S)，使得 peq=0, pfq=0，这两个等式恰好成立。现在假设 ρ是幂等元分离同余的，若eRf,或eΩf，那么ef=e。由推论5，若g∈S(h f,k)，其中，则。由于g∈S(h f,k)，那么同样地，若eLf,或，取g∈S(h ,fk)，可以得到 fg=g,geg=0。

另外，假设 peq≠0,pfq=0，对于eRf,或eLf,结论也成立，证明只需交换e,f，此时不必考虑eΩf;若只考虑 eΩf，取 g ∈S(h,ek)，，其中 h ∈S( p,e), k ∈S(e,q), eg=g,gek≠0,gfk=0。根据推论5，由eΩf，则ge=gf,但是gek=gfk，这就出现矛盾。

相反，ρ不是幂等元分离同余的，通过引理4，存在 e,f∈E(S)，e≠f，使得 eρf,eΩf,eRf，eLf，geg=0成立的充要条件是gfg=0，此时若eΩf,eRf或eLf，而E(S)不是析取的。若e≤f且eΩf，那么，假设存在g∈E(S)有，又 fe=e,则fg=g，所以，且geRgf，但是geρgf的条件是E(S)不是析取的。

定理8 设正则半群S含有零元，若S是同余自由正则半群，则

（1）S是基本逆半群;

（2）E(S)是析取的。

证明：（1）见文献〔1-4〕；（2）由定理7可得。

定理9 设正则半群S含有零元，S是同余自由正则半群的充要条件是S是零单的基本逆半群并且E(S )是析取的〔9-14〕。

证明：必要性由定理7显然;现只需证充分性。若S是0-单的，则S是完全0-单的，那么它必是正则半群，容易发现 |S|>2的同余自由正则半群不是逆半群（即对于析取的定义不是平凡的）。因此有S与含零元的完全零单半群同构即S≅[G ;I,Λ;P]，若 |G|≠1，令(G ,1I,1Λ )对应S上的同余τ，则τ=1S或τ=S×S。再设a∈G且a≠e，由，但所以

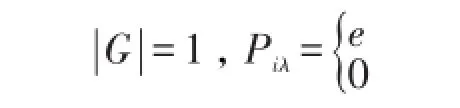
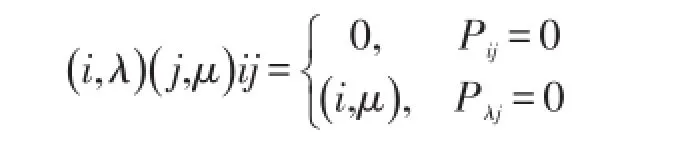
可得S是同余自由正则半群（见〔1〕），但是这里只涉及一个幂等元的情况，若任意e,f,p,q∈E()S，S又是基本的逆半群，E()S是析取的，根据引理4及引理6得S是同余自由正则半群。

〔1〕HOWIE J M.An Introduction to Semigroup Theory〔M〕.New York:Academic Press，1976.

〔2〕MUNN W D.Congruence-free Inverse Semigroups〔J〕. Quart.J.Math，1974，25（2）:463-484.

〔3〕TROTTER P G.Congruence-free Inverse Semigroups〔J〕. Semigroup Forum，1974（9）:109-116.

〔4〕GUO X J,DING J Y,HE X T.Primitive Left Ample Semi⁃groups〔J〕.Journal of Semigroups Theory and Applications，2013，2013（7）:1-9.

〔5〕WANG L M.Congruence-free Regular Semigroups with Q-nverse Transversals〔J〕.Acta Mathematica Sinica：Chinese Series，2002，45（1）:15-20.

〔6〕BAILES G L.Right Inverse Semigroups〔J〕.J.Algebra，1973，26:429-507.

〔7〕PASTIJN F，PETRICH M.Congruences on Regular Semi⁃groups〔J〕.Trans.Amer.Math.Soc.，1986，295:607-633.

〔8〕HALL T E.On Regular Semigroups〔J〕.J.Algebra，1973，24:1-24.

〔9〕龙薇，汪立民.自由单演逆半群上的核-逆算子半群〔J〕.数学学报，2014，57（1）：101-108.

〔10〕冯建.关于完全正则半群同余对的一个公开问题〔J〕.西南大学学报：自然科学版，2009，31（12）：96-99.

〔11〕QIU X W，GUO X J，SHUM K P.Strongly Rpp Semi⁃groups Endowed with Some Natural Partial Orders〔J〕. Journal of Semigroups Theory and Applications，2013，2013（7）：18-29.

〔12〕罗肖强.完全单半群上同余的另一刻画〔J〕.四川文理学院学报，2010，20（2）：20-22.

〔13〕LUO X Q.Π∗-regular Semigroups〔J〕.Bulletin of Mathe⁃matical Science&Applications（India），2012，1（1）：63-70.

〔14〕喻秉钧.平衡范畴与半群的双序〔J〕.数学学报，2012，55（2）：321-340.

（责任编辑 袁 霞）

A Note of Congruence-free Regular Semigroups with Zero Element

LUO Xiaoqiang
（College of Mathematics and Finance-economics,Sichuan University of Arts and Science,Dazhou,Sichuan 635000,China）

In this paper,let S be a regular semigroup,and E(s)be the set of idempotent of regular semigroup S.By constructing the relation between sets in S,we obtain a new method to show the regular semigroup S with zero element is a congruence-free regular semigroup.

regular semigroups;the set of idempotent element;disjunct sets;congruence-free regular semigroups

O152.7

A

1672-2345（2014）06-0007-03

10.3969∕j.issn.1672-2345.2014.06.003

2013-12-22

2014-02-10

罗肖强，副教授，主要从事半群代数理论研究.