基于Petri Net的双臂组合设备故障响应策略的研究*

余华光，白丽平

（广东工业大学机电工程学院，广东广州 510006）

基于Petri Net的双臂组合设备故障响应策略的研究*

余华光，白丽平

（广东工业大学机电工程学院，广东广州 510006）

晶圆制造的加工工艺日趋复杂，组合设备加工模块中存在严格的逗留时间约束以及频繁的故障，因此研究其生产调度，排除出现的故障成为至关重要的问题。通过分析双臂组合设备的并行模块及其加工流程模式，建立能够描述系统的稳态特性的Petri Net模型。基于该模型，当双臂组合设备并行模块出现故障时，分析系统的可调度性，对可调度情况提出有效的运行控制策略，使得晶圆不违反严格的逗留时间约束。最后通过实例验证该控制策略的可行性。

晶圆制造；双臂组合设备；故障响应；Petri Net

1 问题的描述

为了实现晶圆加工，晶圆制造越来越多地采用集成设备，如组合设备(Cluster Tools)，这些技术是晶圆加工的最新体现[1-2]。晶圆制造除了不断进行产品切换外，还需要满足晶圆逗留时间约束[2-4]。自动组合设备中的模块在加工过程中，经常会有各式各样的故障，这是晶圆制造中的另一个难题[5]。本文研究的是晶圆制造中双臂组合设备的故障响应，使得系统故障产生的损失最小，如果可行的话，使双臂组合设备系统不违反约束继续运行。

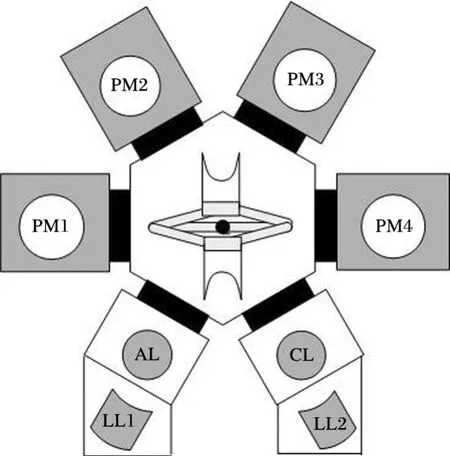
图1 双臂组合设备

组合设备的机械手有单臂、双臂之分[6]，图1所示为具有双臂机械手的组合设备，本文仅讨论双臂组合设备。

在稳态运行时的情况下，组合设备系统可以达到最大生产率[7]。因此，对组合设备的调度和控制主要是稳态下进行，稳态下的系统处于周期性的运行状态。系统中的工作负荷由某些工序进行平衡，则该工序需要设置多个模块同时进行加工，把这些模块称为并行模块。本文利用所提出的Petri Net模型，根据不同的情况，提出了双臂组合设备并行模块的故障响应策略，针对发生故障前后，实现不同稳态的过渡，解决该实际应用中的问题。

2 组合设备的加工过程

设加工流程模式为p（m1，m2，…，mi，…，mn），表示该晶圆组合设备系统共有n个工序，每一个工序的模块数为mi。特别的，本文研究的加工流程为p（1，3，1）。如果mi=1的工序模块发生故障，则系统不能继续运行[8]。其调度策略为：故障后的工序模块可以继续按照发生故障之前的稳态调度策略进行加工，而故障前的工序模块则需将晶圆卸载回真空锁，本文不讨论这种故障情形。因此，本文讨论的对象是：至少存在一个i，满足mi＞1。本文假设：mi=1，i≠2；mi＞1，i=2。两个加工模块一同出现故障的概率接近为零，本文仅讨论的情况是：第2道工序的一个加工模块发生故障。

本文研究的对象是双臂组合设备的周期性稳态的故障响应。限于篇幅，这里简单针对组合设备的加工过程进行说明。令pi表示第i道工序加工模块的集合，p0表示真空锁；令其中一个机械手为G1，另外一个机械手为G2。稳态时，机械手G1旋转到p0的真空锁，将其中一个未加工的晶圆取出并旋转至p1中；然后机械手G2取出p1中加工已经加工完成的晶圆，与此同时，机械手G1将旋转到此的晶圆放置其中进行加工；接下来机械手G2将取出的晶圆旋转至p2，机械手G1将p2中加工完成的晶圆取出，与此同时，机械手G2将旋转至此的晶圆放置其中进行加工；如此依次进行循环，直至一个机械手G1（或G2）将pn的晶圆取出，另外一个机械手G2（或G1）将持有晶圆放置pn进行加工，接下来该机械手G1（或G2）将持有晶圆放置回p0真空锁。

3 Petri Net建模

根据Petri Net的特性，为准确描述双臂组合设备的晶圆加工过程，本文采用有限容量的Petri Net。用库所pi表示第i工序的加工模块，用⊚图形表示，并且有K() pi=mi，表示pi模块中可以共同加工mi个晶圆，同时用p0表示真空锁，并且有K() p0=∞，表示真空锁没有晶圆数量的限制；机械手用库所r○表示，两个晶圆同时被抓取，所以K() r=2；在双臂组合设备生产过程中，机械手在某个变迁完成后需要一定的等待时间，这一事件用库所qij(i∈Nn，j=1，2，3，4)表示，图像上的表示与r○相同，但是K() qij=1。特别的，赋时库所q01表示从pn卸载的晶圆进入p0准备将加工完成的晶圆进行卸载，而非赋时库所q04表示机械手从真空锁p0装载晶圆准备旋转至加工工序p1。当库所qij中含有一个标识时，表示机械手在加工模块中进行等待或者是持有晶圆进行交换。模型中的所有变迁都用“——”来表示，其中用sij(i∈Nn，i=1，2)来表示在库所pi中进行晶圆交换；在真空锁中的变迁s01、s02表示赋时库所，其中s01表示卸载加工完成的晶圆，而s02表示载入未加工的晶圆。

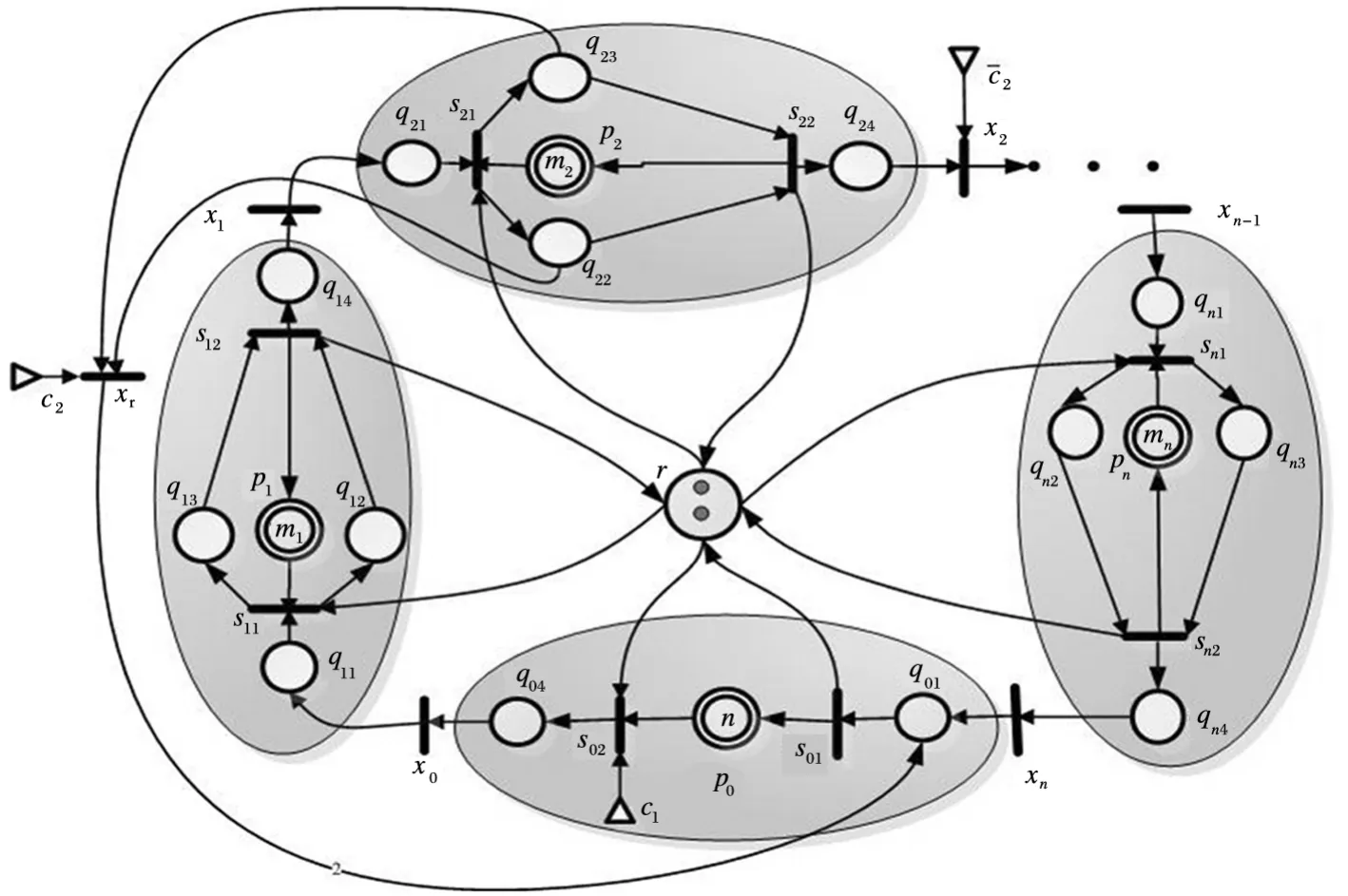
图2 双臂组合设备Petri Net模型

根据以上模型说明，建立相应的双臂组合设备Petri Net模型，如图2表示。为了避免模型出现死锁，在模型中增加了控制库所c，用图形∆来表示，其中采用u1（u为c的控制函数）来控制稳态情况下的死锁问题，采用u2来控制发生故障情况下的死锁问题。控制函数分别为：

4 系统可调度性分析

当非并行模块发生故障，其调度策略上述已有所提及。而当某工序的其中一个并行模块发生故障时，由于该工序少一个模块，双臂组合设备的晶圆加工流程模式随即发生改变，故障模块中的晶圆逗留时间τi也随之改变，不能保证原来调度的可行性。这时需要判定发生故障后的系统可调度性，并且尽量减少损失；如果系统可继续调度，需要分析是否需要调整之前的调度，怎样调整，甚至是系统如何从发生故障前的稳态过渡到故障后的稳态。

赋予相应Petri Net中库所和变迁的时间如表1所示。

按照之前的假设，第2道工序为并行模块，即m2＞1，第i道生产工序的节拍以θi表示，机械手的节拍以Ψ 表示。在稳态Θ=Θ1=Θ2=…=Θn=Ψ 时，并且为最小节拍，则该系统达到最优调度[4]。

按照本文的假设，晶圆加工流程为p(m1，m2，…mn)，则在故障出现之前有：

每个工序的加工下界和上界：

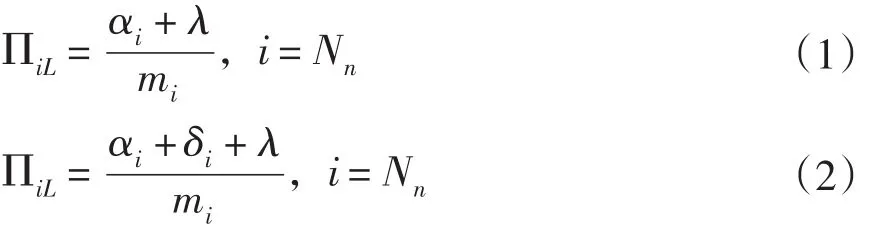
晶圆逗留时间：

其中，机械手周期时间为：

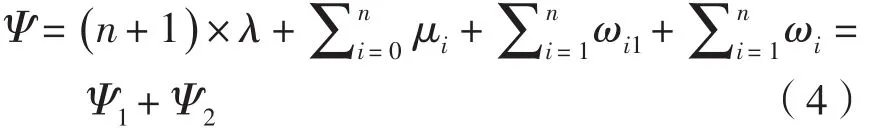
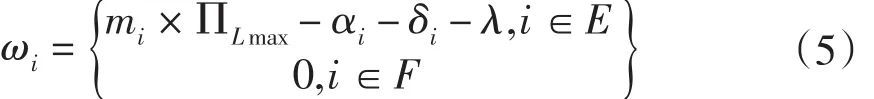
表1 库所与变迁的时间描述

结论1：双臂组合设备是可以调度的，若满足如下条件之一：

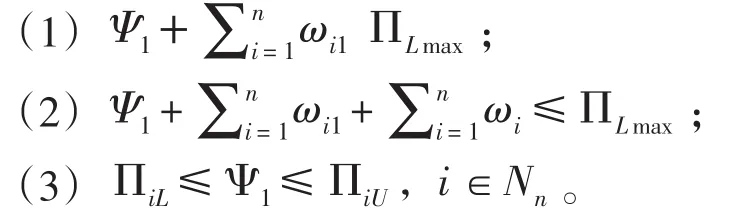
在发生故障之前，结论1中的一个条件必定满足，如果存在着一组ω1，ω2…，ωn、ω11，ω21，…，ωn1的值，那么系统是可调度的[9]。在文献[9]中给出了在加工时间和机械手操作时间确定的条件下，最优调度的方法才可求得。

当工序 p2中的一个模块发生故障，ΓiL和ΓiU分别表示故障后第i道工序生产节拍的下界与上界，从第i道工序卸载晶圆之前的机械手等待时间以ϕi表示，i∈Nn。当i≠2时，有ΓiL=ΠiL， ΓiU=ΠiU；当i=2，有

晶圆逗留时间：

其中，机械手周期时间为：

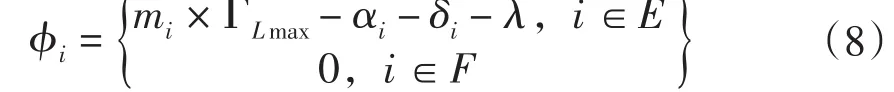
故障出现后，机械手任务时间Ψ1并不改变。根据上述结论1，出现故障后可以有以下结论。

结论2双臂组合设备是可以调度的，若满足如下条件之一：

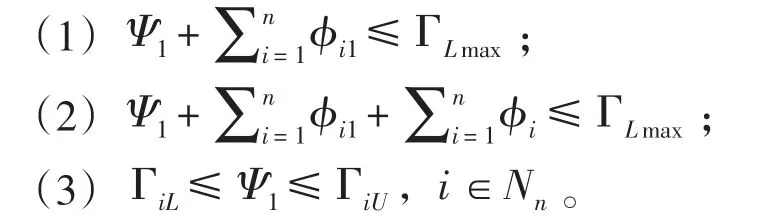
由上述分析可知，机械手在出现故障前后的交换等待时间ωi和ϕi是不相同的，即使发生故障后系统仍是可调度的，发生故障前后的稳态调度也是不同的。所以，解决该问题的关键是准确衔接这两个不同的稳态调度。

5 故障响应策略

故障响应的关键是：在保证所有的约束得到满足的情况下，各个事件的发生怎样去控制，使系统平稳的从发生故障前周期性的稳态调度过渡到发生故障后周期性的稳态调度。本文假设当工序2的一个加工模块出现故障后，则该工序成为瓶颈。

令为故障前工序i中晶圆的允许逗留时间窗，故障后工序2中的晶圆的允许加工逗留时间窗为。根据故障前后情形的不同，可以分为下列几种情况：（1）发生故障后，机械手等待时间ϕi=0的可调度情形；（2）发生故障后，机械手等待时间ϕi≠0的可调度情形；（3）发生故障后，不可调度情形。限于篇幅，本文只针对情形一进行讨论并举例验证。

情形一

这种情形是系统在发生故障后系统依然可调度的，并且故障后的机械手的等待时间ϕi=0，即满足于：发生故障前为结论1中的条件（1），发生故障后为结论2中的条件（1）。如图3所示是这种情形下的示意图。

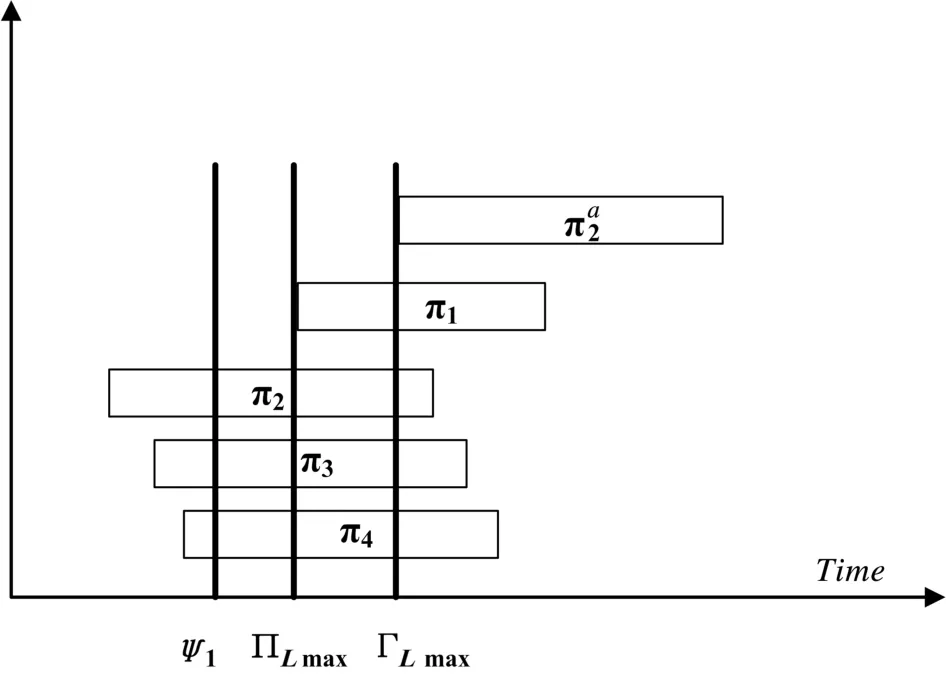
图3 故障情形1的示意图

此时Γ2L=ΓLmax为系统的生产节拍。发生故障前后没有改变的是机械手任务时间Ψ1，但是ΓLmax＞ΠLmax，意味着在这种条件下，发生故障后的系统仍是可调度的，但故障发生前后的稳态调度并不一样。如果发生故障后保持之前的调度，则第2道工序的加工晶圆在未完成之前就会被取出。所以，系统需要一个故障响应控制策略，使得系统在发生故障之后，在满足晶圆逗留时间约束的条件下，能从发生故障前的稳态调度平稳地过渡到发生故障后的可行稳态调度。下面给出相应的故障响应策略。

响应策略：发生故障后按照如下规则对系统进行控制。

故障后，取出的是一个从故障模块中非正常完成的晶圆，那么接着触发xr。若非这一步，则按照故障前的调度策略进行调度。并且直到机械手取出故障模块中的晶圆，触发xr为止。

用G(x0)表示触发xr后引发x0的次数。故障后，如果G(x0)≤m2-1，那么按照故障发生之前的稳态调度进行。如果G(x0)＞m2-1，那么，设置ϕi=0，和通过Φ2=Φ-ψ1赋值给非零变量ϕi1，并且满足于

定理：如果组合设备系统满足上面给出的情形1的条件，那么响应策略1满足于系统从发生故障前的可行稳态调度平稳地过渡到发生故障后的可行稳态调度，并且不违反在生产变换过程中严格的晶圆逗留时间约束要求。

证明：按照之前的条件，由ωi=0，和通过Ψ2=Ψ-Ψ1赋值给非零变量ωi1，并且满足于实现了故障前的调度，由ϕi=0，和通过Φ2=Φ-Ψ1赋值给非零变量ϕi1，并且满足于实现了故障后的调度，并且故障前后的稳态调度都是可行的。在两个稳态进行切换的时候，p1，p2，…，pn中都正在进行加工一枚晶圆，而这些晶圆是按照发生故障前的稳态调度载入的，这些晶圆如果不违反逗留时间约束，那么该定理成立。根据式子（3），对i∉2，有τi=Γ2L-λ-ωi≤ΠiU-λ-ωi=αi+δi，即故障后的晶圆逗留时间小于允许的晶圆逗留时间，故可以在不违反严格的晶圆逗留时间约束的基础上，从故障前稳态调度过渡到故障后的稳态调度。即该定理成立。

6 实例

实例：假设自动组合设备的晶圆加工流程模式为p（1，3，1），各加工时间参数为：λ为10 s， u0=u1=8 s， u2=u3=5 s， α1=60 s，α2=170 s， α3=55 s， δ1=25 s， δ2=45 s，δ3=30 s。

针对该例子，得出Π1L=70，Π1U=95，Π2L=60，Π2U=75，Π3L=65，Π3U=95，ϕ1=66，因此，发生故障前的稳态生产节拍为ΠLmax=Π1L=70，Π1U＞ΠLmax=Π1L，Π3U＞ΠLmax=Π1L，ψ1＜ΠLmax，满足可调度条件。通过π=Ψ=70，Ψ2=70-Ψ1=4，因此，满足故障前稳态的可调度情形 ω1=ω2=ω3=0， ω21=0， ω11=ω31=2是可以实现的。若并行模块发生故障，即m2=2。对于故障后Γ2L=90，Γ2U=112.5，发生故障后的稳态生产节拍为 ΓLmax=Γ2L=90，ϕ1＜ΓLmax，满足可调度条件。通过πa=ϕ=90，Φ2=90-ϕ1=24，因此，满足故障后稳态的可调度情形ϕ1=ϕ2=ϕ3=0，ϕ21=0，ϕ11=ϕ31=12是可以实现的。

由情形1的响应策略得知，发生故障触发xr后，在引发s11之前，并且满足G() x0＞2，在q11中的令牌等待时间从ω11=2切换为ϕ11=12。第一工序晶圆的逗留时间从切换前的τ1=60变为切换到ς1=80。因为80∈(60，95)，所以该工序的晶圆不违反逗留时间约束。第二道工序的晶圆逗留时间从切换前的τ2=200变为切换到ς2=170。因为170∈(170,215)，所以该工序的晶圆不违反逗留时间约束。第三道工序的晶圆逗留时间从切换前的τ3=60变为切换到ς3=80。因为80∈(55,85)，所以该工序的晶圆不违反逗留时间约束。从上述各工序看出，该调度策略使得系统在发生故障切换后满足晶圆逗留时间约束，从而实现从一个周期性的稳态调度平稳地过渡到另外一个周期性的稳态调度，并且只损失故障模块中的晶圆。

7 结束语

本文介绍了双臂组合设备的晶圆加工过程，针对双臂组合设备的并行模块出现故障后的不同情形，分析了该系统发生故障前后的不可调度的运行控制方法和可调度性最优过渡。并且通过实例验证情形一的响应策略的可行性。双臂组合设备的并行模块发生故障后的响应策略作为本文的研究对象，对于具有重入的或者多组合设备的故障响应，有待于进一步的研究。

［1］KIM J H.Stable schedule for a single-armed cluster tool with time constraints［C］.Proceedings of the 4th IEEE Conference on Automation Science and Engineering. Washington，D.C.USA：IEEE，2008：97-102.

［2］ROSTAMI S，HAMIDZADEH B.An optimal residen⁃cy-aware scheduling technique for cluster tools with buf⁃fer module［J］.IEEE Transact ions on Semiconductor Manufacturing，2004，17（1）：68-73.

［3］LEE T E，PARK S H.An extended event graph with neg⁃ative places and tokens for timed window constraints［J］.IEEE Transactions on Automation Science and En⁃gineering，2005，2（4）：319-332.

［4］WU Naiqi，CHU Chengbin，CHU Feng，et al.A Petri net method for schedule ability and scheduling problems in single-arm cluster tools with wafer residency time con⁃straints［J］.IEEE Transactions on Semiconductor Man⁃ufacturing，2008，21（2）：224-237.

［5］YAO X D，EMMANUEL F G，MARCUS S I.Optimal preventive maintenance scheduling in semiconductor man⁃ufacturing［J］.IEEE Transactions on Semiconductor Manufacturing，2004，17（3）：345-356.

［6］LEE T E.A review of scheduling theory and methods for semiconductor manufacturing cluster tools［C］.Pro⁃ceedings of the 40th Conference on Winter Simulation.Mi⁃ami， Fla， USA： WinterSimulation Conference，2008：2127-2135.

［7］LOPEZ M J，WOOD S C.Systems of multiple cluster tools configuration，reliability and performance［J］. IEEE Transactions on Semiconductor Manufacturing，2003，16（2）：170-178.

［8］LEE T E，LEE H Y，PARK D B.Scheduling analysis of timed constrained dual-armed cluster tools［J］.IEEE Transactions on Semiconductor Manufacturing，2003，16（3）：521-534.

［9］WU Naiqi，CHU Chengbin，CHU Feng，et al.An ana⁃lytical algorithm for schedule ability analysis and optimal scheduling of single-arm cluster tools with wafer residen⁃cy time constraints［C］.Proceedings of 2008 IEEE In⁃ternational Conference on Networking，Sensing and Con⁃trol.Washington， D.C.， USA： IEEE， 2008：224-237.

Failure Response Policy for Dual-Arm Cluster Tools Based on Petri Net

YU Hua-guang，BAI Li-ping
（College of Mechanical and Electrical Engineering，Guangdong University of Technology，Guangzhou510006，China）

Since there are many sojourn time constraints and failure in the processing module of cluster tools in semiconductor industry，processing technology for wafer manufacturing becomes more and more complicated.Thus，it is extremely important to study schedule feasibility to eliminating the failures in manufacturing process.This paper analyzed the processing flows of the parallel module for a cluster tool with a dual-arms robot，and developed a Petri Net model for this cluster tool that can describe the steady state characteristics of the whole system.With this PN model，if there are failures appearing in parallel modules，it can analyze the schedule conditions and feasibility，and propose some effective control strategies for different failures’conditions such that these strategies can satisfy wafer sojourn time constraints at the same time.Finally，we illustrate the proposed analysis and method through several examples.

semiconductor manufacturing；dual-arm cluster tools；failure response policy；Petri net

TP391 F406

：A

：1009－9492(2014)10－0020－05

10.3969/j.issn.1009-9492.2014.10.006

余华光，男，1988年生，广西桂林人，硕士研究生。研究领域：晶圆制造、Petri Net。

(编辑：阮 毅)

*国家自然科学基金（编号：60574066）

2014－04－01