混沌差分进化算法在复杂优化问题中的应用研究

肖文显，许利军，马孝琴

差分进化算法［1］(differential evolution，简称DE)，是由Storn和Price于1995年共同提出的一种基于群体智能的启发式优化算法.该算法通过群体内不同个体间的合作与竞争指导优化搜索，具有控制参数少、收敛速度快等特点.近年来，DE算法以其计算的鲁棒性、稳定性被广泛应用于诸多领域［2－4］.然而，差分进化算法在应用时随着进化的不断深入及群体多样性下降，极易导致算法陷入局部最优.混沌优化算法(chaos optimization algorithm，简称COA)是一种新型的直接搜索优化算法，算法搜索过程按照混沌运动的自身特性进行，在搜索时具有遍历和非重复的特性，具有较高的搜索效率，因此得到广泛的应用［5－7］.

论文将DE算法和COA算法相耦合，提出了混沌差分进化算法(chaos differential evolution algorithm，简称CDEA).该算法利用混沌映射(Logistic映射)产生的序列能不重复地遍历一定范围内的所有点的特点，弥补差分进化算法容易陷入局部最优的缺陷，从而提高算法的全局搜索性能.最后，通过若干典型函数和TSP问题对改进算法的优化效果进行测试，结果证明了论文算法的可行性和有效性.

1 标准差分进化算法

差分进化算法是一种基于群体差异的启发式随机搜索算法，通过种群内个体间的合作与竞争来实现对优化问题的求解.标准DE算法的基本操作包括变异、交叉和选择3种算子.算法首先在问题的可行解范围内随机初始化种群，X0= ［X01，X02，…，X0NP］，NP为种群个体数目，上标0表示为初始种群.个体x0i=［x0i，1，x0i，2，…，］表征问题的一个解，i为个体编号，D为解链长度.算法通过利用种群个体间的差异性，依次进行变异和交叉操作完成对种群个体的进化，随后以贪婪选择的原则进行种群个体的优选.

算法的基本思想是:按式(1)对第g代种群中编号为i的个体Xgi进行变异操作，得到变异体Vgi+1;然后按式(2)对变异体进行交叉操作，产生试验个体Ugi+1;对于最小化问题，基于贪婪思想按式(3)进行选择操作产生新个体.

其中:r1，r2，r3∈{1，2，…，NP};Xgr1为父代基向量;(Xgr2－Xgr3)为父代差分向量;F为缩放因子;g为迭代代数;CR为范围在0～1之间的交叉概率;行()为在0～1范围内生成的随机数;j行为{1，2，…，D}之间随机选取的随机量;f(·)为适应度函数.

2 混沌差分进化算法

2.1 混沌差分进化算法的思想

由于种群多样性在进化后期迅速下降，标准DE算法极易陷入局部最优而造成“早熟”.而混沌优化法具有随机性和遍历性的特点，可以较好地弥补DE算法的上述缺陷.因此，有研究者考虑将两种优化方法进行耦合，从而得到一种新的优化算法［8－9］.但是，这些耦合算法仅利用混沌映射对解空间进行混沌搜索，即突出全局搜索能力.论文在此基础上进一步利用混沌算法的随机性和遍历性，在进化过程中和进化结束后分别进行混沌扰动，加强算法的局部寻优能力，从而达到平衡全局搜索与局部寻优的目的.

论文所提出的CDEA算法包含3个基本点:一是，将混沌映射(Logistic映射)产生的混沌序列映射到待求解问题的解空间中，以这些通过映射转换后的混沌序列作为DE算法的初始解;二是，对每个经过变异、交叉和选择操作所得到的个体进行混沌扰动，得到新的个体;三是，将寻优得到的全局最优解进行混沌扰动，在该点进行局部深度搜索.

2.2 混沌差分进化算法的设计

(1)编码设计

利用CDEA算法求解复杂优化问题时采用实数编码，待求解问题的初始解群体以染色体序列X0=［X01，X02，…，X0NP］的形式表示，其中:个体x0i=［x0i，1，x0i，2，…，x0i，D］表征问题的一种可行解.

(2)混沌映射

采用一维Logistic模型来设计混沌映射，其迭代方程为

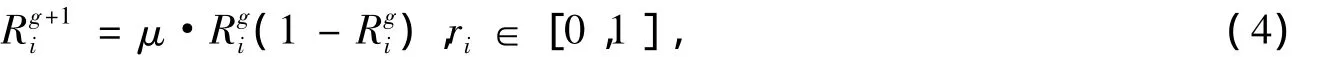
其中:Rgi为混沌变量，表示由混沌方程产生的［0，1］之间的某个数，且R1i∈［0，1］;g为迭代次数;μ为控制参数，且0≤ μ ≤4.当 μ ＞ 3.57，R1i∈［0，1］且 R1i≠ {0.25，0.5，0.75}时，序列将在(0，1)内永不重复地“游荡”，不向任意点收敛且敏感地依赖于初始点.

(3)初始解生成

随机生成NP个数据点R1i，其中:i=1，2，…，NP.分别以这些数据点为初始点按式(4)的混沌映射方式进行迭代，得到NP个混沌序列Ri=［R1i，R2i，…，］，D为问题维数.对于每个Ri按式(5)映射到待求解问题的解空间.由此，得到问题的初始解集X0=［X01，X02，…，X0NP］，其中:个体 x0i=［x0i，1，x0i，2，…，］.

(4)进化过程中的混沌扰动机制

对第g代种群XNP×D进行扰动，操作如式(6)、(7)所示.

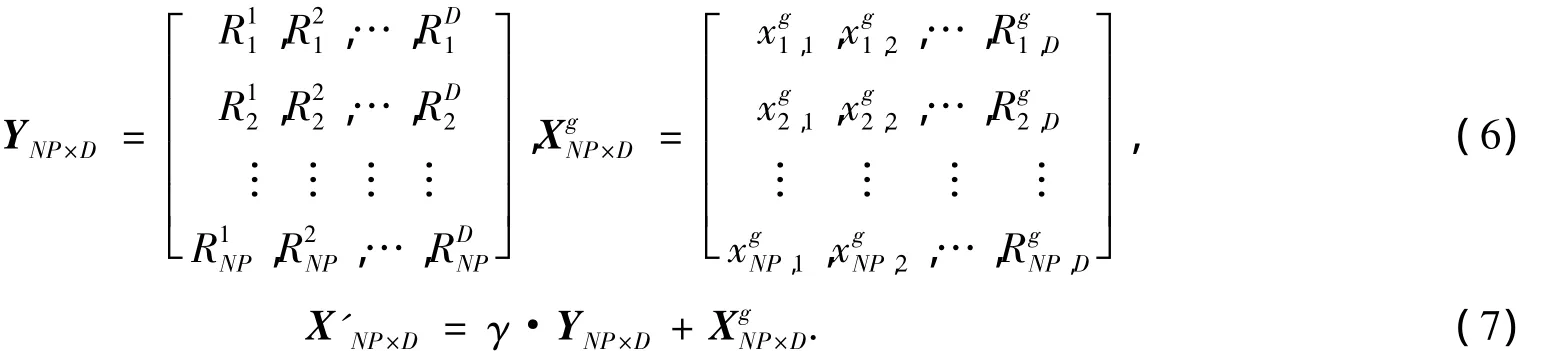
其中:YNP×n为D个混沌时间序列构成的矩阵;γ为扰动步长;X'NP×D为经扰动产生的新种群.

(5)对求得最优解的混沌扰动机制

对求得的最优解增加一个微小的混沌扰动，进行局部深度搜索.可以通过如下步骤:设ω为当前求得的最优解x*=(x*1，x*2，…，x*D)映射到［0，1］区间后的决策向量，ωk为对ω迭代k次后所得到的向量.通过式(8)进行动态扰动，便可得到扰动后的新决策向量ω'.

其中:α为(0，1)之间的一个数值，按式(9)进行动态取值，在进化早期α较大，可进行全局搜索，进化后期，α较小，重点进行当前最优解小范围内的深度搜索;k为迭代次数;m为一个正整数，取2.

(6)算法迭代终止判断

所设迭代终止条件如下，满足其中任意条件即可结束寻优迭代:

(i)连续若干代最优适应值不变化;

(ii)迭代次数达到最大迭代次数.

2.3 求解步骤

混沌差分进化算法求解的计算步骤如下:

步骤1 根据待求解问题确定决策变量和解的取值空间;

步骤2 参数设定:确定种群规模NP、缩放因子F、交叉概率CR、控制参数μ、扰动步长γ以及参数m;

步骤3 随机选取NP个不同的初值，根据Logistic模型生成初始混沌序列，并按式(5)将其映射到待求解问题的解空间中;

步骤4 按式(1)～(3)进行变异、交叉和选择操作;

步骤5 对求得的新种群中的每个个体进行式(6)、(7)所示的扰动操作，比较扰动前后个体的适应值，取较优者进入新一代种群;

步骤6 判断种群是否收敛，若未收敛，则返回步骤4;若已收敛，则进入步骤7;

步骤7 对当前最优解进行如式(8)、(9)所示扰动，取扰动前后适应值更优者作为最终的全局最优解，算法结束，输出结果.

3 计算机模拟仿真

3.1 测试函数仿真

为验证改进算法的可行性和有效性，采用如下测试函数对上述算法进行对比测试:

Schwefel函数

Rastrigrin函数

实验设置的参数如下:函数维数D=5，种群规模NP=40，最大迭代次数为100，缩放因子F=0.65，交叉概率CR=0.6，控制参数μ=4，扰动步长γ=0.1，参数m=2;分别采用COA、DE以及CDEA对上述测试函数进行40次优化计算，取优化结果的平均值、最优值、标准差和运行时间作为衡量指标，结果如表1所示.

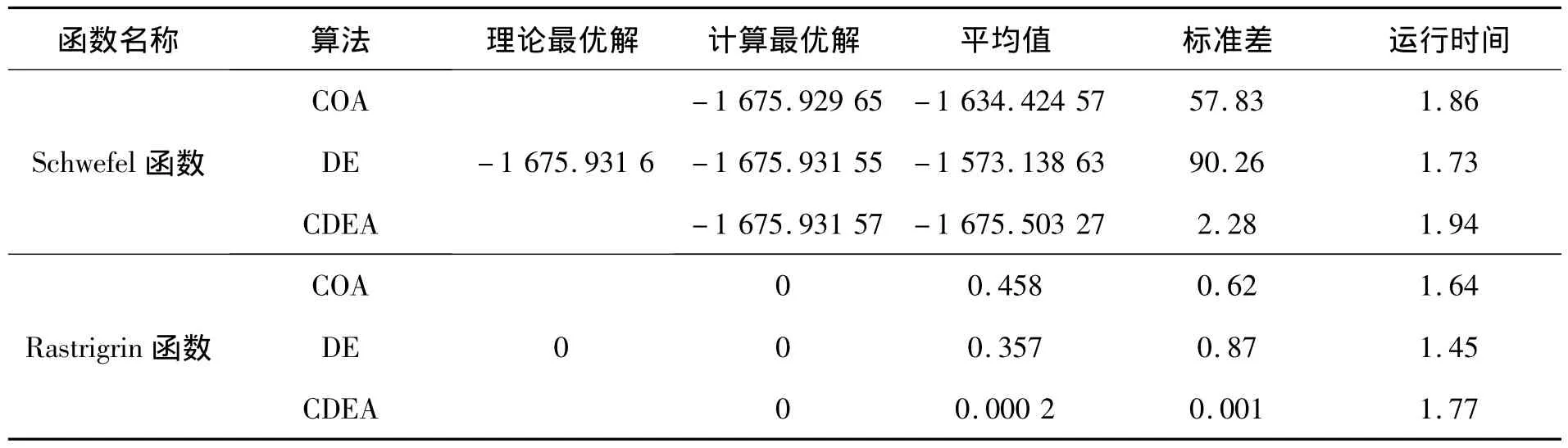
表1 优化结果对比Tab.1 Comparison of optimal result

由表中数据可见，与COA和DE相比，CDEA的求解结果均优于前两者，这正说明CDEA具有较强的全局寻优能力.对比不同算法求解结果的标准差可以发现，CDEA的标准差最低，这也反映出CDEA算法求解稳定性优于COA和DE.对比3种算法的运行时间，CDEA略长于另外两种算法，但相差不大.这是由于CDEA在算法结构上比前两者更加复杂、求解耗时相对会有一定增加的缘故.求解时间的略微增加带来的影响与求解性能的大幅提升相比，基本可以忽略不计.因此，CDEA在寻优能力和求解稳定性上均优于COA和DE.

3.2 TSP 问题

测试函数可以在一定程度上检测算法的可行性和高效性，然而付诸实际应用，仍需进一步检验.因此，对于OliverTSP30个城市(已知最优解为423.74)和TSP50个城市(已知最优解为427.86)，分别采用DE和CDEA进行求解，参数设置与3.1中相同.

表2为TSP问题运算20次的平均结果.对比可以发现，CDEA对TSP问题的求解所得的最优解精度要高于COA和DE算法，且平均寻优能力也强于另外两个算法.对比TSP30和TSP50两问题的求解结果可以发现，CDEA在求解较为复杂的问题时，寻优效果比COA和DE更加明显.上述结论与3.1中测试函数模拟结果所反映的情况一致，再次印证了论文所提出的CDEA算法的有效性.

表2 TSP30和TSP50问题20次运行结果Tab.2 The results of 20 iterations between TSP30 and TSP50

4 结束语

论文将差分进化算法和混沌优化方法耦合，利用混沌序列的遍历性和内部迭代的随机性，弥补差分进化算法容易陷入局部最优的缺陷，从而提高算法的搜索性能，避免算法的早熟收敛.对CDEA的核心思想和基本设计框架进行了阐述，并从数学测试函数和实际问题两方面对其求解性能进行验证.针对典型函数的测试结果表明:与DE和COA相比，CDEA算法的全局搜索性能有了显著提高，能有效避免算法陷入局部最优.在TSP问题中的应用表明，论文提出的CDEA算法在求解实际问题时，依然具有较高的实用性和有效性.CDEA算法求解具有高效性和稳定性优点，适用于求解复杂的优化问题.

［1］ Rainer S，Kenneth P.Differential evolution a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997(11):341 －359.

［2］ Kim H，Chong J，Park K.Differential evolution strategy for constrained global optimization and application to practical engineering problems［J］.IEEE Transactions on Magetics，2007，43(4):1565 －1568.

［3］ 方强，陈德钊，俞欢军，等.基于优进策略的差分进化算法及其化工应用［J］.化工学报，2004，55(4):598－602.

［4］ 郑慧涛，梅亚东，胡挺，等.双层交互混合差分进化算法在水库群优化调度中的应用［J］.水力发电学报，2013，32(1):54－62.

［5］ 李兵，蒋慰孙.混沌优化方法及其应用［J］.控制理论与应用，1997，14(4):613－615.

［6］ 李新杰，胡铁松，郭旭宁，等.0－1测试方法的径流时间序列混沌特性应用［J］.水科学进展，2012，23(6):875－882.

［7］ 娄素华，吴耀武，熊信银.电力系统无功优化的变尺度混沌优化算法［J］.电网技术，2005，29(11):20－24.

［8］ 卢有麟，周建中，李英海，等.基于混沌搜索的自适应差分进化算法［J］.计算机工程与应用，2008，44(10):31－33.

［9］ 谭跃，谭冠政，涂立.一种新的混沌差分进化算法［J］.计算机工程，2009，35(11):216－217.