基于上三角域上的形状控制重心混合有理插值

赵前进，朱六三

近年来，基于连分式的二元有理插值方法被广泛关注.檀结庆在文献［1－2］中通过对Newton多项式插值和Thiele型连分式插值进行加工，用类似于张量积的方法构造了Newton－Thiele和 Thiele－Newton两种二元混合有理插值.赵前进在文献［3］中通过对插值节点集进行分块，构造了基于块的混合有理插值.但连分式插值会受到可能有不可达点、偏逆差商不存在等瓶颈问题的制约，另外，连分式插值无法避免极点同时又难以控制极点的位置.1945年，Taylor发现了多项式插值的重心公式;1984年Werner给出了重心有理插值方法［4］.利用权的符号可判定重心有理插值在插值区间内的极点个数，通过适当选择权可使重心有理插值避免极点和不可达点［5］.而对于二元重心插值一直存在着图像控制问题，文献［6］作者在矩形域上利用偏导数对图形有效地在y轴单方向上进行形状控制，即y=y0且对x的偏导数大于零(或小于零)时，改变重心权从而有效地调节图像.论文将文献［6］方法应用于上三角域的重心——牛顿复合插值［7］，结合文献［8］中Lebesgue常数最小建立优化模型.给出的实例表明，此方法所得的二元有理插值继承了重心有理插值的计算量小、数值稳定性好、没有极点以及可以避免不可达点等优点，又能有效地对形状进行有效的局部控制.

1 基于上三角网格的重心——牛顿混合插值

网格点分布如下

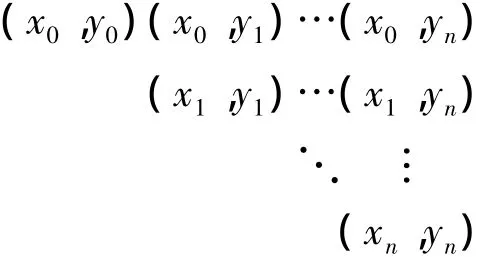
上述网格点被称作上三角网格，记作SU.

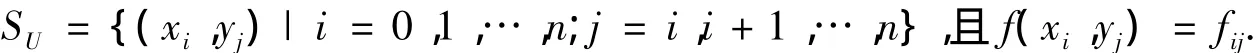
构建有理插值函数

插值函数的构造:

定义

其中

(c)wi(i=0，1，…，n)分别为 x0，x1，…，xn对应的插值权，满足

最优权wi(i=0，1，…，n)可由Lingo优化软件求出.

2 二元重心公式的偏导数

二元重心公式可以写成

或

这样就可以得出偏导数公式［6］

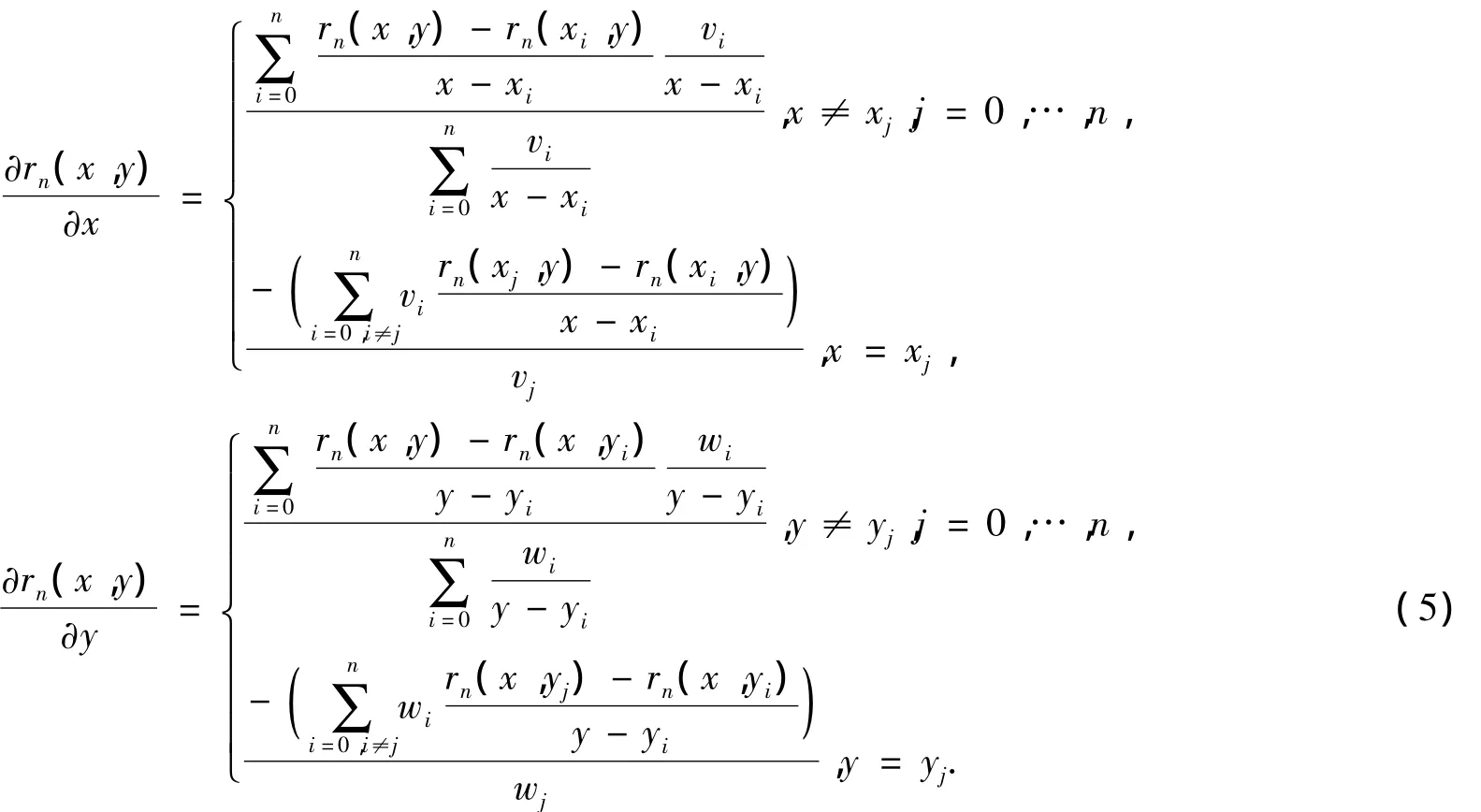
偏导数能作为求权约束条件，能有效地调节双变量重心有理插值形状［1］.

3 基于Lebesgue常数最小的形状控制重心有理插值优化模型

因为重心有理插值取得插值函数是由插值权决定其插值效果，所以就得找到最优权.下面就来建立使用该方法的优化模型.

以插值节点处的权wi(i=0，1，2，…，n)为决策变量，以Lebesgue常数最小，即

最小为目标函数，以有理函数R(x，y)无不可达点、无极点为约束，增加权的规范化约束条件和偏导数符号为约束条件，建立如下优化模型求解最优权

最后使用Lingo优化软件计算出最优权.

4 数值实例

例1 给定上三角域数据如下

记上三角网格上基于Lebesgue常数最小为目标函数用牛顿——重心有理插值为R1(x，y)

加入偏导数和不加偏导数在y=0.3和y=0.5的形状变化，如图1～3所示.

图1 R1(x，y)Fig.1 R1(x，y)

图2 R2(x，y)Fig.2 R2(x，y)

图3 R3(x，y)Fig.3 R3(x，y)

5 结束语

论文在插值点基于上三角网格的重心——牛顿有理插值法、加以偏导数作为约束条件并利用Lebesgue常数最小为目标函数求得最优权方法，继承了重心有理插值的计算量小、数值稳定性好、没有极点以及可以避免不可达点等优点，由例子图像可直观看出通过偏导数对上三角域上局部调节效果明显，说明该方法在上三角域上应用是可行的.

［1］ Tan J.Bivariate blending rational interpolants［J］.Approx Theory ＆ its Appl，1999，15(2):74-83.

［2］ Tan J，Fang Y.Newton-Thiele's rational interpolants［J］.Numerical Algorithms，2000(24):141-157.

［3］ Zhao Q J，Tan JQ.Block based Newton － like blending rational interpolation［J］.Journal of Computational Mathematics，2006，24(4):515-526.

［4］ Schneider C，Werner W.Some new aspects of rational interpolation［J］.Math Comp，1986，175(47):285-299.

［5］ Schneider C，Werner W.Hermite interpolation:the barycentric approach［J］.Computing，1991，46(1):35-51.

［6］ Hoa T N，Annie C，Oliver SC.Shape control in multivariate barycentric rational interpolation［J］.AIP Conf Proc，2010，543:1281.

［7］ Zhao QJ，Du JL.The new bivariate rational interpolation over the triangular grids［J］.Computer Science and Automation Engineering，2012:780-784.

［8］ Zhao O J，Wang B B，Fang X W .Lebesgue constant minimizing shape preserving barycentric rational interpolation optimization algorithm［J］.Science ＆ Technology Vision，2013(3):30-32.