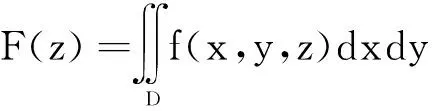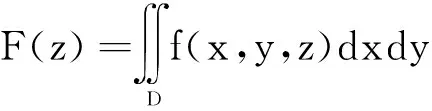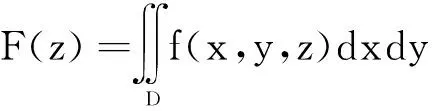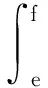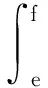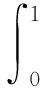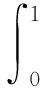利用投影法选取重积分的上、下限
2014-02-09郭新
郭 新
(濮阳职业技术学院数学与信息工程系,河南濮阳,457000)
在计算二重积分和三重积分这样的重积分时,一般都是先将它们化成相应的累次积分。在化的过程中,往往要用到投影法确定积分的上、下限,然后再运用定积分的计算方法来计算。
一、二重积分上、下限的选取
即
从中可以看到,二重积分的上、下限实际上是定积分的上、下限与被积函数f(x,y)。
二、三重积分上、下限的选取
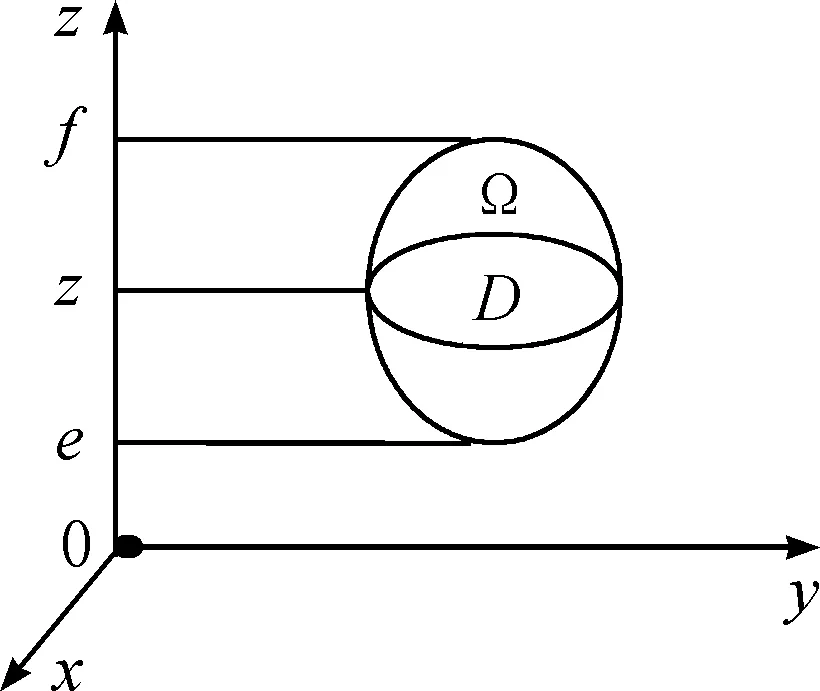
在直角坐标系下对三重积分进行计算,在将三重积分化为累次积分时,可以使用坐标面投影法和坐标轴投影法,具体方法的使用还要看实际问题的情况,适合哪个方法就用哪个方法。
(一)坐标面投影法
如图1,闭区域Ω={((x,y,z)|z1(x,y) 图1 坐标面投影法 过任意点(x,y)作一条平行于Z轴且垂直穿过闭区域Ω的直线,该直线与区域Ω的边界至多有两个交点z1(x,y)和z2(x,y)。这种区域类型称为XY型空间区域。 计算方法如下: (1)将x,y当作常量,那么三元函数f(x,y,z)就变成只关于变量z的一元函数。由定积分的积分法可得 (2)把Ω投影在xoy平面上,得到平面区域D,结合二重积分和积分法可得 D={((x,y)|a (3)化三重积分为累次积分为 同理我们可以得到yz型和xz型空间区域及它们的算法。 如图2,闭区域Ω={((x,y,z)|e 图2 坐标轴投影法 具体方法如下: 把积分区域Ω投影到坐标轴Z,得到投影区间z∈[e,f],取∀z∈[e,f],作平行于xoy面且过点(0,0,z)的平面,得到它们的截面,则三重积分可化为 再在平面区域D上,对变量x,y进行二重积分的计算,得到 从而得到 例:求平面x+y+z=1与三坐标面所围成的四面体的体积。 解:由题意知,四面体在xy平面上的投影是直线x=0,y=0,x+y=1,所围成的三角形平面区域D,则 投影法是数学思想方法中的化归思想在积分学中的直接运用,也是微元分析法的本质规律在公式化方法中的彰显。它不仅易于接受和掌握,而且可以拓展到极坐标系、柱面坐标系、球面坐标系下使用。 [1] 程红萍,钟忠銮.高等数学:第三版[M].上海:同济大学出版社,2012. [2] 刘玉琏.数学分析讲义[M].北京:高等教育出版社,2003. [3] 常瑞玲.利用投影法选取积分的上、下限[J].濮阳职业技术学院学报,2008(1).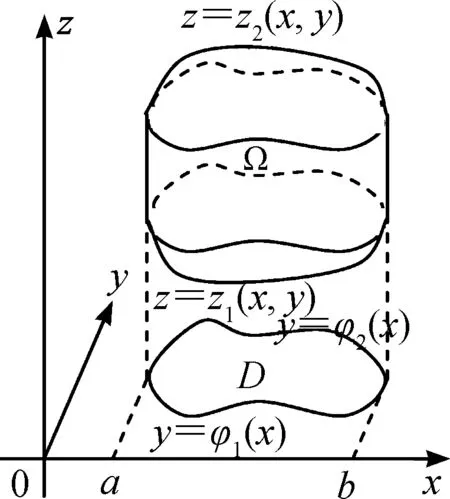
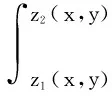

(二)坐标轴投影法