基于CFD方法求取供应船位置水动力导数回归公式

柯枭冰，罗薇，赵小仨，徐海祥

1 武汉理工大学高性能船舶技术教育部重点实验室，湖北武汉430063

2 武汉理工大学交通学院，湖北武汉430063

0 引 言

人类自进入工业时代以来，物质财富极大地增长，但陆上资源和能源供应却日趋紧张，文明的可持续发展还有赖于陆地经济向海洋经济的转型。而海洋环境复杂多变，海洋资源和能源的开发有其特殊的困难，需要先进的技术和设备作为支撑，其中动力定位技术就是海洋开发技术的一个典型代表。

供应船作为动力定位技术的常用船型，其使用日益增加。在建立供应船的运动数学模型时，需要确定模型中的水动力导数，本文将主要研究其中的位置水动力导数的求取方法。

在船舶设计阶段，确定船舶水动力导数的方法一般有：经验公式法、约束模试验法、理论和数值计算法，以及自航模试验（实船试验）加系统辨识法。其中经验公式法最方便、快捷，但使用范围有一定的限制，对于合适的船型，所得到的结果能够达到工程需要的精度。由于动力定位供应船一般都装有呆木，目前，还未见有关这一类船型的水动力导数经验公式方面的文献。

鉴于此，本文将通过船型变换生成系列供应船船型，采用CFD 方法计算系列供应船型的位置水动力导数Yv和Nv，再采用多元回归分析建立位置水动力导数关于船型参数的回归公式，以为设计阶段供应船水动力导数的求解提供一定的参考。

1 数值计算方法

1.1 坐标系

坐标系如图1 所示。其中，o 点位于船舯，纵轴x 的正方向指向船艏，横轴y 的正方向指向左舷，按照右手法则，z轴正向垂直向上。

图1 随船坐标系Fig.1 Coordinate system on board

1.2 控制方程

对三维粘性不可压缩的N-S 方程和连续性方程进行时均化处理［1］，得到

式中：ui为平均速度分量，其中u1=u，u2=v，u3=w，i 和j 的取值范围为（1，2，3）；p 为平均压力；ρ 为流体密度；Fi为体积力；μ 为流体动力粘性系数；为雷诺应力项。式（2）即为雷诺时均N-S 方程，简称RANS 方程。

1.3 湍流模型

2 KVLCC2 计算验证

2.1 计算模型与网格划分

为验证本文计算方法的有效性，首先使用该方法计算ITTC 推荐的船型KVLCC2 在斜航状况下所受的水动力［2-3］，并与INSEAN 水池斜航试验结果［4］进行对比。KVLCC2 船型的主要几何参数如表1 所示，其中船模缩尺比为45.714。

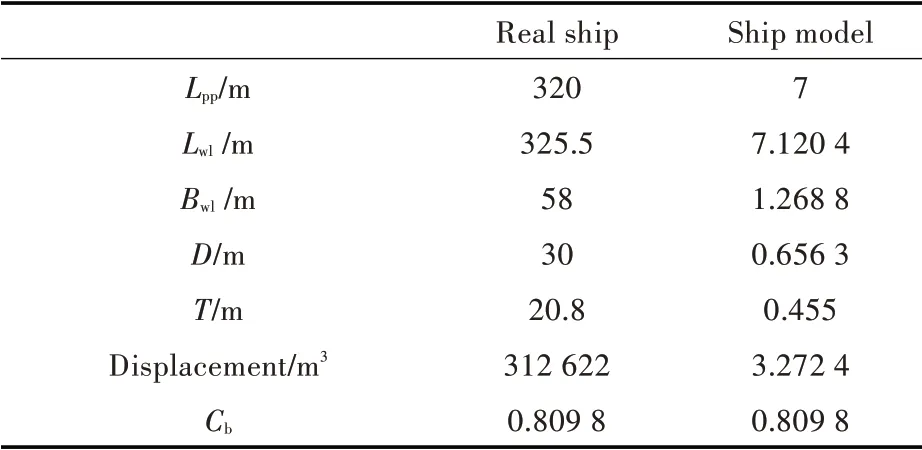
表1 KVLCC2 船模主要参数Tab.1 The main parameters of KVLCC2 model

计算域如图2 所示。在上游1.5LPP处建立入流面；下游3LPP处建立出流面；左、右边界距船模中纵剖面各为1.5LPP，水深吃水比h/T=8.3，傅氏数Fn=0.064。

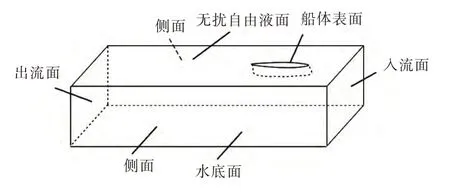
图2 计算域Fig.2 The computational domain

KVLCC2 船的艉部因有艉轴出口，因而在全船划分结构化网格难以实现。可在船艉处划分非结构化的四面体网格，其余各处采用分块结构化网格，如图3 所示。网格数共413.5 万。在界层内，使用Boundary Layer 命令划分多层网格来捕捉船模边界层内的流动。

2.2 边界条件及数值计算方法

所谓边界条件，是指在计算域的边界上，所求解的变量或者一阶导数随地点和时间变化的规律。本文边界条件设置如下［1］：

1）入流面及左、右表面：VELOCITY_INLET；

图3 艏、艉部网格Fig.3 Grids of bow and stern

2）流动出流表面：OUTFLOW；

3）船体表面：WALL；

4）计算域的上、下表面：SYMMETRY；

5）分块划分结构化网格时，块与块之间重合而分属不同的块的面：INTERFACE。

湍流模型选取SST k-ω 模型，压力速度耦合选取SIMPLEC 算法，压力插值采用Standard 格式，动量、湍动能和湍流耗散率插值采用Second Order Upwind 格式。

2.3 计算结果及分析

保持x 方向速度不变，变化y 方向的速度来形成不同的漂角（v=U sin β，其中v 为横向速度，U为纵向速度）。根据相对运动原理，船模位置保持不变，水流以一定的速度流向船模［5-6］。基于FLUENT 软件平台，计算不同漂角下船舶所受的横向力Y 和转艏力矩N。本文计算了0.268°，0.55°，1.05°，1.8°和3.8°这5 个不同漂角下各船型的横向力Y 和转艏力矩N，计算结果与INSEAN 水池约束模型试验数据的对比如图4 所示。

图4 KVLCC2 船模CFD 结果与试验数据对比Fig.4 The comparison of CFD data and experimental data of KVLCC2 model

由图4 可以看到，横向力Y 的计算值与试验值吻合良好，误差较小。在1.05°时，试验值出现了微小的波动，而计算值则比较平稳，这可能是因为数值模拟受到的干扰没有试验状态下的复杂，比较符合实际情况。转艏力矩N 在小角度（0.268°，0.55°，1.05°）时，其数值计算结果与试验值吻合良好，而在稍大角度（1.8°，3.8°）时二者的间隔则较大，但总体趋势还是一致的［7-8］。

3 系列船型计算方案

3.1 系列船型生成

变换的母型船为一艘75 m 的动力定位供应船，船模缩尺比为20，主要几何参数如表2 所示，供应船侧视图如图5 所示。

表2 供应船的主要参数Tab.2 The main parameters of supply vessel

图5 动力定位供应船Fig.5 Dynamic positioning supply vessel

对50 条供应船进行了统计，其主要参数取值范 围 为：3.2＜L/B＜5，9.5＜L/d＜20，2.5＜B/d＜4.5，0.6＜Cb＜0.8 。在船型变换过程中，保持排水量和船长不变，呆木相对于船模中纵剖面的位置和面积也均保持不变，变换的模型利用Maxsurf 软件生成。变换方案［9-10］如表3 所示。

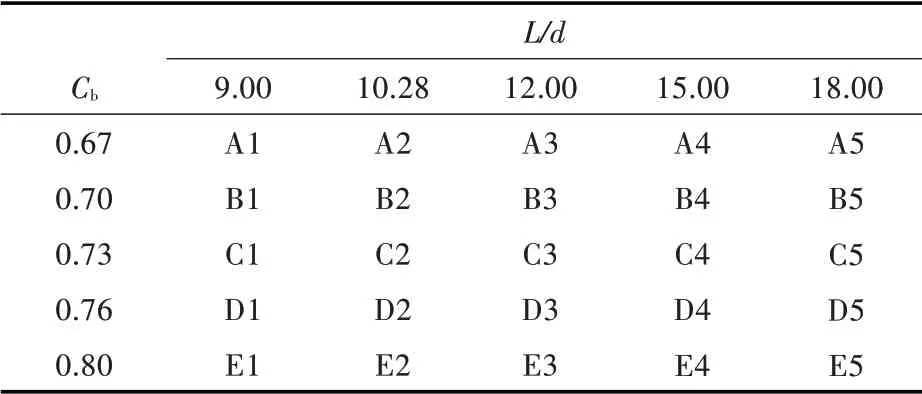
表3 船型变换方案Tab.3 Hull form transformation scheme

在生成的25 个系列船型（除去母型船共24个）中，减去吃水过小和过大的船型，并将非常接近的方案取其中之一后，剩下的13 个船型即为需要进行计算的模型。

3.2 系列船型计算结果及无因次化

系列船型的斜航数值计算方法及步骤与验证的船型KVLCC2 相同，仅在设置计算参数时考虑了各自船型的不同特点。需要说明的是，在划分网格时，13 个船型均采用的是结构化网格划分方法，其分块方式与网格节点分布一致，并保证y+值在一定的范围内以保证网格相似性。

下面，以方案A1 为例来说明求取水动力导数的步骤。

根据船舶水动力导数的物理意义，可以由表4所示的不同漂角β（横向速度）下船模所受的横向力和力矩来求取位置水动力导数Yv和Nv。以A1船为例，其在不同横向速度下的横向力和力矩曲线如图6 所示。分别求取Y 关于v 的曲线和N 关于v 的曲线在零点的切线的斜率，该斜率值即为对应的水动力导数。

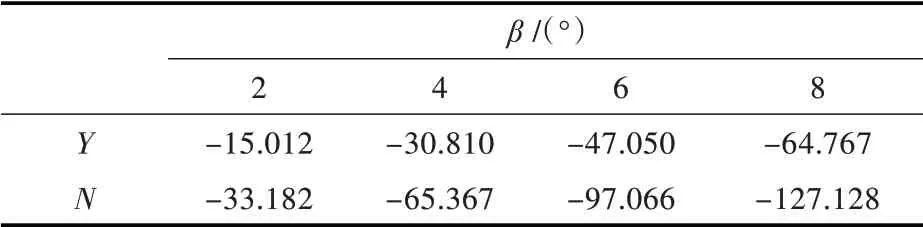
表4 方案A1 的横向力Y 与转艏力矩N 计算结果Tab.4 Computational results of Y and N of hull form A1

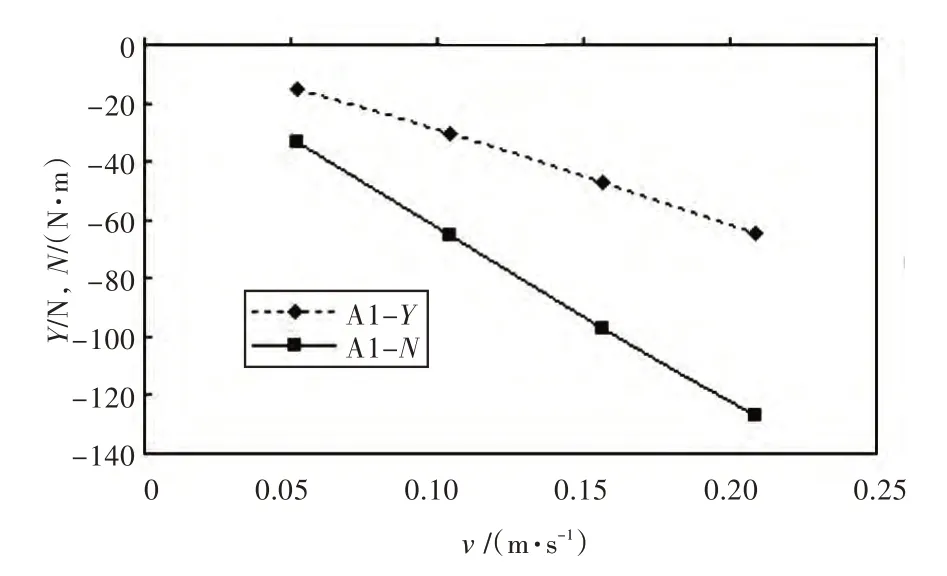
图6 A1 船的横向力Y 和力矩NFig.6 Y and N of hull form A1

根据以上方法求取其它船型的位置水动力导数，并将结果进行无因次化，如表5 所示。其中，无因次化的规则为：

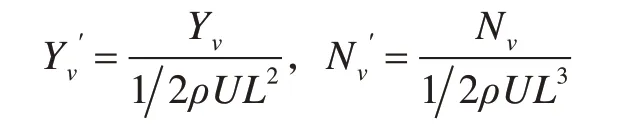
式中：U 为x 方向的速度；L 为船长。

4 位置水动力导数回归公式

根据表5 中各船型的水动力导数无因次值，进行多元线性回归，分析拟合位置水动力导数的回归公式［11-12］。首先，进行相关性分析。直接选取B/d，L/B，L/d，Cb为自变量进行拟合，则各变量的相关性如表6 所示。

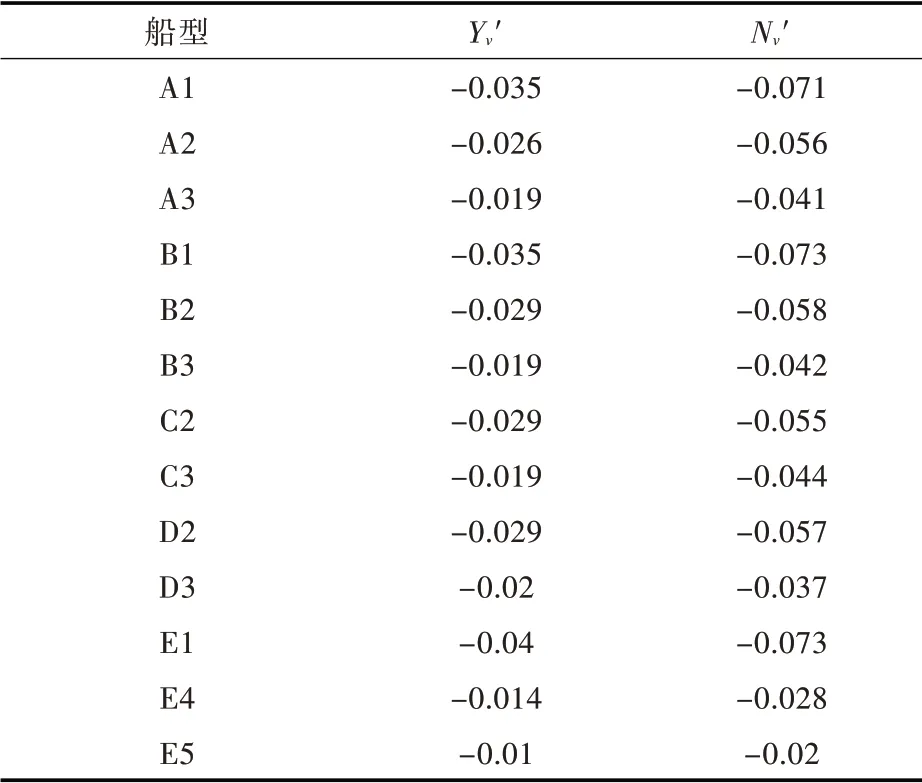
表5 系列船型的位置水动力导数无因次值Tab.5 Computational results of Yv′ and Nv′

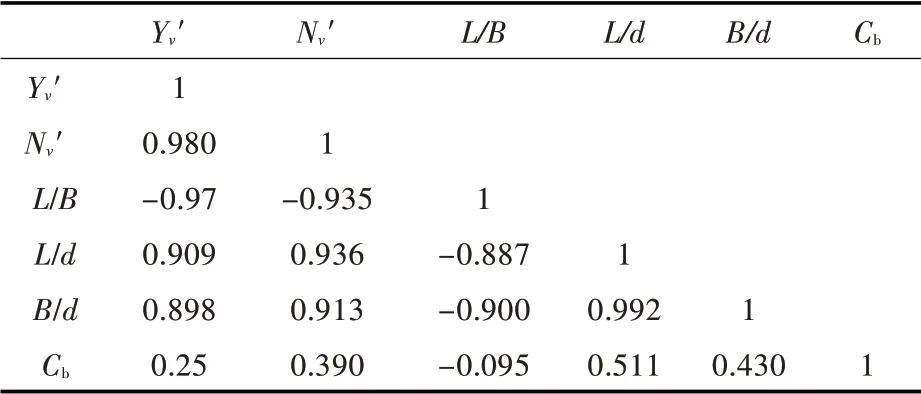
表6 相关性分析（自变量为B/d，L/B，L/d，Cb）Tab.6 Correlation analysis（independent variable：L/d，L/B，B/d，Cb）

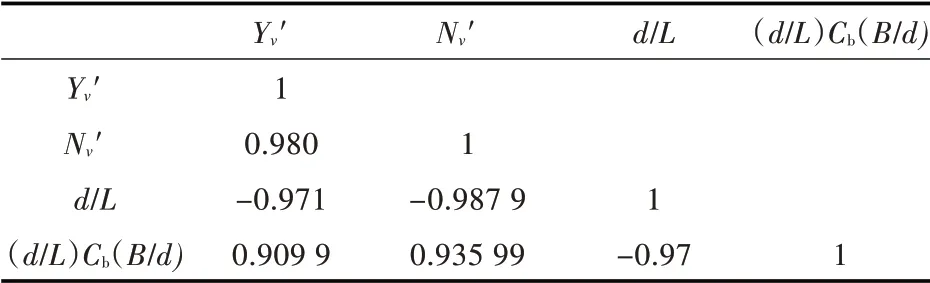
表7 相关性分析（自变量为d/L 和（d/L）Cb（B/d））Tab.7 Correlation analysis（independent variable：d/L，（d/L）Cb（B/d））

下面，将给出由全部13 个样本点拟合的回归公式：

为了检验回归公式的拟合质量，先取12 个样本点进行公式拟合，然后再用余下的那个样本点进行检验。余下的样本点是参数较为居中的B3。表8 给出了B3 的和根 据12个样本点回归公式预测的值与CFD 计算的或值的比较。

表8 回归公式质量验证Tab.8 Quality validation of regression formula

由表中的误差项可以看出，最小二乘法拟合公式的预测值与CFD 计算值相比，误差较小，可以认为将样本点进行最小二乘法回归是合适的。

5 结 语

本文对动力定位船舶位置水动力导数的CFD回归方法进行了研究：

首先，基于FLUENT 软件平台计算了KVLCC2 船的斜航流场，得到了横向力和转艏力矩，经与INSEAN 水池试验数据进行对比，证明用CFD 方法计算船舶斜航流场是有效的。

然后，通过船型变换技术得到动力定位供应船（装有呆木）的不同船型，并采用与上述相同的数值方法计算其不同漂角下的斜航流场，通过最小二乘法拟合得到位置水动力导数Yv和Nv以及其无因次值。

最后，通过多元线性回归，得到了动力定位供应船位置水动力导数关于参数和的回归公式。初步验证回归公式拟合质量良好，证明对位置水动力导数的结果进行线性回归是合理的。求取的回归公式可为设计阶段供应船位置水动力导数的确定提供简便的方法。

［1］王福军.计算流体动力学分析：CFD 软件原理与应用［M］.北京：清华大学出版社，2004.

［2］田喜民，邹早建，王化明. KVLCC2 船模斜航运动功粘性流场及水动力数值计算［J］.船舶力学，2010，14（8）：834-840.TIAN Ximin，ZOU Zaojian，WANG Huaming. Compu⁃tation of the viscous flow and hydrodynamic forces on a KVLCC2 model in oblique motion［J］. Journal of Ship Mechanics，2010，14（8）：834-840.

［3］杨勇.非定常操纵运动船体水动力数值计算［D］.上海：上海交通大学，2011.

［4］Workshop on Verification and Validation of Ship Ma⁃neuvering Simulation Methods［EB/OL］.（2008-04-16）.［2013-03-15］. http：//www.simman2008.dk/KV⁃LCC/KVLCC2/tanker2.html.

［5］李冬荔，杨亮，张洪雨，等. 基于CFD 方法的船舶操纵性能预报［J］. 武汉理工大学学报，2009，31（24）：120-123.LI Dongli，YANG Liang，ZHANG Hongyu，et al.Predic⁃tion of ship maneuverability based on CFD method［J］.Journal of Wuhan University of Technology，2009，31（24）：120-123.

［6］李冬荔，杨亮，聂武. 操纵运动船舶的水动力计算研究［J］.船舶工程，2009，31（2）：8-11，23.LI Dongli，YANG Liang，NIE Wu.Computational inves⁃tigation of hydrodynamic forces around maneuvering ship［J］.Ship Engineering，2009，31（2）：8-11，23.

［7］刘山. 基于CFD 技术数值模拟平面运动机构试验［D］.武汉：武汉理工大学，2012.

［8］杨波，万林，王骁，等.纯横荡和旋臂试验的数值模拟［J］.舰船科学技术，2008，30（4）：138-141.YANG Bo，WAN Lin，WANG Xiao，et al. Numerical simulation of pure sway and rotating arm test［J］. Ship Science and Technology，2008，30（4）：138-141.

［9］王银. 舰船方案设计中的耐波性预报模型研究［D］.哈尔滨：哈尔滨工程大学，2012.

［10］项久洋，毛筱菲. 基于主要尺度要素的船型变换［J］.中国舰船研究，2008，3（4）：15-18，25.XIANG Jiuyang，MAO Xiaofei. The hull variation based on the main hull parameters［J］. Chinese Jour⁃nal of Ship Research，2008，3（4）：15-18，25.

［11］袁益雷. 基于新细长船兴波阻力理论的系列60 阻力图谱之拓展研究［D］. 哈尔滨：哈尔滨工程大学，2008.

［12］杨盐生.船舶阻力系数和推力系数计算的数据库方法［J］.大连海事大学学报，1995，21（4）：14-17.YANG Yansheng. Calculating ship resistance and thrust coefficient based on database［J］. Journal of Dalian Maritime University，1995，21（4）：14-17.

［13］方崇智，萧德云. 过程辨识［M］. 北京：清华大学出版社，1988.