巧算面积 妙解图形——面积法在“勾股定理”中的应用

曹 霞（江苏省南京市29中致远校区）

面积法是几何题解法中的一种基本方法，就是利用面积相等，来建立关于面积的等式或方程，从而求解、证明题目的一种方法.此方法在苏科版八年级数学“勾股定理”的应用中尤为常见.

面积法是一种古老的传统证明方法，早在一千多年以前，三国时期的数学家赵爽在《周髀算经》中就利用“玄图”中的等积问题巧妙地证明了勾股定理.

如图1，因为SABCD=c2，SABCD=SEFGH+4S△AGD=（a-b）2+4×ab

所以c2=（a-b）2+4×ab.

c2=a2-2ab+b2+2ab.

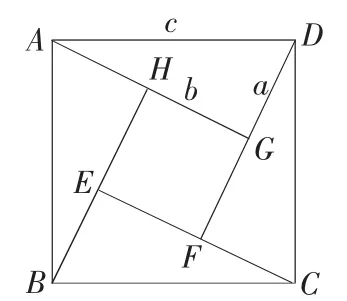
图1

所以a2+b2=c2.

美国第20 任总统加菲尔德利用图2 给出了勾股定理的另一种证明，由于用了梯形面积公式和三角形面积公式，从而使证明更加简洁，在数学史上被传为佳话.

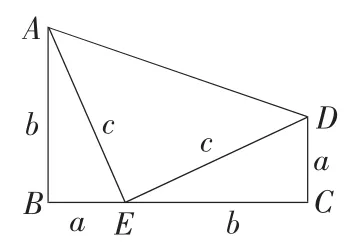
图2

如图2，因为SABCD=（a+b）（a+b）=（a+b）2，

SABCD=S△ABE+S△ECD+S△AED=ab+ab+c2

（a+b）2=ab+ab+c2，a2+2ab+b2=2ab+c2

所以a2+b2=c2.

在勾股定理的400 多种证明方法中，用“面积法”证明代数式之间的恒等关系式，即具有严密性，又具有直观性，是数学中以形证数、数形结合的典范.

而在勾股定理应用的解题中，巧用面积法，往往会带来意想不到的简便.

例1 如图3，△ABC 中，∠ACB ＝90°，AC ＝7，BC ＝24，CD⊥AB 于D.

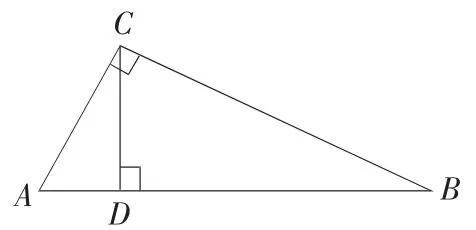
图3

（1）求AB 的长；

（2）求CD 的长.

解：（1）因为在Rt△ABC 中，∠ACB=90°，

所以AB2=AC2+BC2=72+242=252.

所以AB=25.

（2）因为S△ABC=AC·BC=×7×24，

S△ABC=A B·CD=×25×CD，

例1 是利用面积法，解决几何线段计算问题的典型代表.解题中抓住△ABC 面积的两种不同表示，建构等量关系，列出方程求解线段CD.给我们的启发是，面积法是几何计算中的一个重要等量关系，当已知条件有多个垂直关系时，我们要关注某一图形面积的不同表示.

例2 如图4，有一个直角三角形纸片，两直角边AC=6，BC=8，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，点C 与点E 重合，你能求出CD 的长吗？

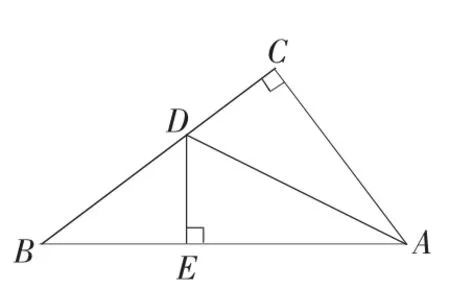
图4

（1）常规解法

解：因为在Rt△ABC 中，∠ACB=90°，

所以AB2=AC2+BC2=62+82=102.

所以AB=10.

因为△ACD 折叠得△AED，

所以CD=ED，AC=AE=6，∠AED=∠ACD=90°.

所以BE=AB-AE=10-6=4.

设CD 为x，则ED=x，BD=8-x，

所以在Rt△BDE 中，x2+42=（8-x）2.

所以x=3，即CD=3

（2）面积法

解：因为在Rt△ABC 中，∠ACB=90°，

所以AB2=AC2+BC2=62+82=102.

所以AB=10.

因为△ACD 折叠得△AED，

所以CD=ED，AC=BE=6，∠AED=∠ACD=90°.

设CD 为x，则ED=x，BD=8-x

因为S△ABD=AC·BD=×6×（8-x）=24-3x，

S△ABD=AB·ED=×10×x=5x，

所以24-3x=5x.

所以x=3，即CD=3.

例2 的常规解法，抓住Rt△BDE，利用“勾股定理”建构直角三角形三边的等量关系，列出方程求解线段.这种解题方法学生掌握主要有两点困难：①在Rt△BDE 中利用勾股定理建立方程需要线段BE、DE、BD，这三条线段都需要求出或用未知数x 表示，特别是线段BE 的求值，对中下等学生来说比较困难.②列出的方程x2+42=（8-x）2比较复杂，化简转化为一元一次方程的过程同样对还未接触二次方程的初二学生来说有一定的困难.而利用面积法解例2，抓住△BDA 面积的两种表示方法建立方程，其中线段AB、BD、DE 的表示都比较容易，减少了转化的环节，且列出的方程直接就是一个一元一次方程，所以解方程得过程也比较简单.本题也可以抓住△BCA 的面积解题：

S△BCA=AC·BC=×6×8=24，S△BCA=S△BDA+S△DCA=×6x+×10x=8x，则8x=24，x=3，即CD=3.

例3 如图5，折叠长方形ABCD，使点D 落在边BC 上的点F 处（折痕为AE）.已知AB=DC=6 cm，AD=BC=10 cm.求EC 的长.

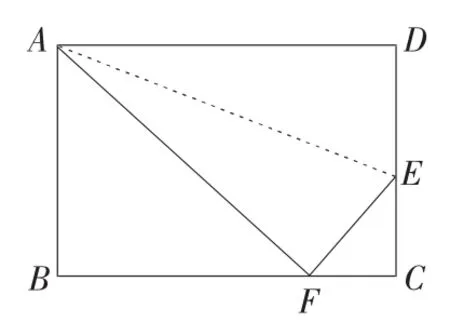
图5

（1）常规解法

解：设CE 为x，则DE=6-x，

因为△ADE 折叠得△AFE，

所以AF=AD=10，DE=EF=6-x，∠AFE=∠ADE=90°.

因为在Rt△ABF 中，∠ABF=90°，

所以BF2=AF2-AB2=102-62=82.

所以BF=8.

所以CF=BC-BF=10-8=2.

因为在Rt△ECF 中，∠C=90°，

所以EF2=CF2+CE2.

所以（6-x）2=22+x2.

（2）面积法

解：设CE 为x，则DE=6-x

因为△ADE 折叠得△AFE，

所以S△ADE=S△AFE，AF=AD=10.

因为在Rt△ABF 中，∠ABF=90°，

所以BF2=AF2-AB2=102-62=82.

所以BF=8.

所以CF=BC-BF=10-8=2.

因为SAFED=SABCD-S△ABF-S△FCE=6×10-×8×6-×2x=36-x

SAFED=2S△ADE

所以36-x=60-10x.

面积法解例3，从割、补两种不同的角度表示四边形AFED的面积，建立了比较简单的一元一次方程，解题过程的简洁.

例4 如图6，在Rt △ABC中，∠BCA ＝90°，点D 是BC 上一点，AD ＝BD=5，若AB ＝8，求CD 的长.

（1）常规解法

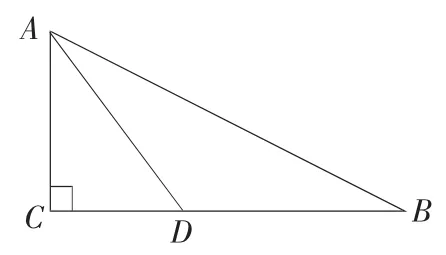
图6

解：设CD 为x，则BC=5+x，

因为在Rt△ABC 中，∠ACD=90°，

因为AB2=AC2+BC2，AC2=82-（5+x）2，

因为在Rt△ACD 中，∠ACD=90°，

所以AD2=AC2+CD2，AC2=52-x2

所以52-x2=82-（5+x）2.

（2）面积法

解：如图7，过点D 做DE⊥AB 于E，

因为AD=BD，

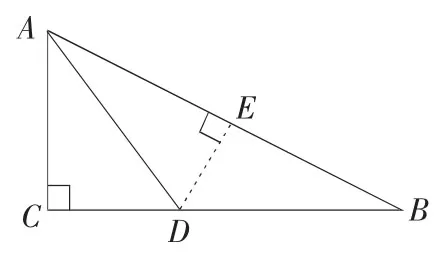
图7

因为在Rt△AED 中，∠AED ＝90°，

所以DE2=AD2-AE2=52-42=32.

所以DE=3.

S△ABD=BD·AC=×5×AC，S△ABD=AB·ED=×8×3，

因为在Rt△ACD 中，∠ACD ＝90°，

所以CD2=AD2-AC2=52-

例4 用常规方法解，没有一个直角三角形的三边能够全部求出或用未知数表示，所以无法直接用“勾股定理”建立方程.而是抓住线段AC 在两个直角三角形中的不同表示建立方程，难度较大.且所列出的方程52-x2=82-（5+x）2比较复杂，也造成了学生的解题困难.面积法解例4，已知条件不具备多个垂直关系，所以需要添加辅助线，而等腰三角形的条件提醒我们可以做底边上的高.

例5 如图8，正方形ABCD 的边长为5，E 在BA 上，且AE=2，F在BC 上，且CF=1，过D 作DG⊥EF于G，求DG 的长.

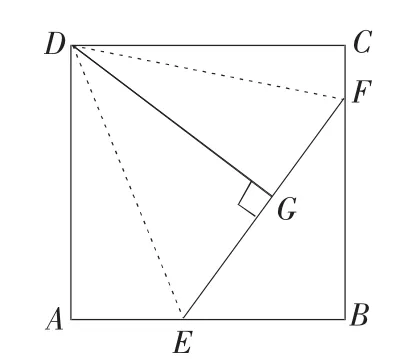
图8

（1）常规解法

解：连接DE、DF，

BE=AB-AE=5-2=3，BF=CB-CF=5-1=4，

因为在Rt△BFE 中，∠B ＝90°，

所以FE2=BE2+BF2=32+42=52

所以FE=5.

同理得DE2=29，DF2=26，

设EG 为x，则GF=5-x，

因为在Rt△DGF 中，DG2=26-（5-x）2.

在Rt△DGE 中，DG2=29-x2，

所以29-x2=26-（5-x）2.

因为在Rt△DGE 中，DG2=26-（5-x）2=

（2）面积法

解：连接DE、DF，

BE=AB-AE=5-2=3，BF=CB-CF=5-1=4，

因为在Rt△BFE 中，∠B ＝90°，

所以FE2=BE2+BF2=32+42=52.所以FE=5.

S△DEF=E F·DG=×5×DG.

S△FED=SABCD-S△ABE-S△FCD-S△FBE=52-×5×2-×5×1-×3×4=.

利用面积法解，避免了用勾股定理解题的繁难计算，使解题过程十分的简单.

通过以上例题可以发现，面积法解几何题，要抓住其特征：①当已知条件中有多个垂直条件时，我们就应该考虑到面积法；②单图形沿边找高，有两条高的图形要关注；③复合图形可以抓住其面积等它各部分面积之和（差），从整体和部分两种不同的角度，或者分割和填补两种不同的方法，表示同一图形的面积，建立方程.利用面积法解决直角三角形中较复杂的几何计算问题，思路简洁，方程简单，所以我们应多关注.