以“共顶正方形”为模型的中考试题及变式探究

☉宁夏中卫市沙坡头区宣和镇张洪学校 张 宁

以“共顶正方形”为模型的中考试题及变式探究

☉宁夏中卫市沙坡头区宣和镇张洪学校 张 宁

一、基本模型

例1 （2008年广东省初中数学竞赛）如图1，正方形ABCD的边长为2，点E在边AB上.四边形EFGB也是正方形，设△AFC的面积为S，则（ ）.

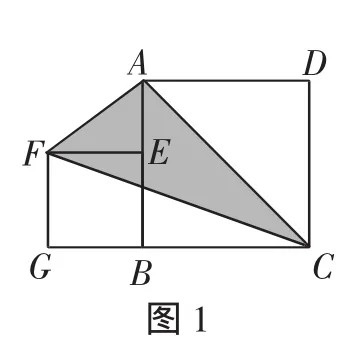
A.S=2 B.S=2.4

C.S=4 D.S与BE的长度有关

解析：设正方形BEFG的边长为a，则AE=2-a，CG=2+a.

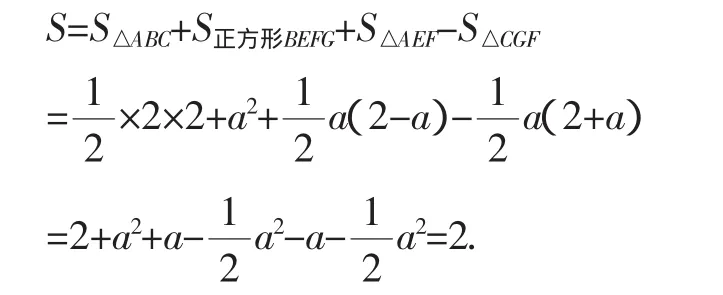
点评：本题以两个具有一个公共顶点的正方形为基本模型，主要考查了正方形的性质、三角形面积的求法等知识.由于△AFC的面积不易直接求得，故采用间接求法：利用某些特殊图形的面积来表示△AFC的面积，这种方法是求不特殊图形的面积的一种重要方法.在表示△AFC的面积的过程中，还需要有正方形BEFG的边长，因而这里又体现了“设而不求”的解题方法.从解题过程来看，△AFC的面积与正方形EFGB的边长无关.本例中所涉及的几何图形简洁优美，内涵丰富，不妨称之为“共顶正方形”，即有公共顶点的正方形称之为“共顶正方形”.

二、以“共顶正方形”为模型的中考试题

1.以“共顶正方形”为模型，求阴影部分的面积

例2（2012年湖北潜江市）如图2，线段AC=n+1（其中n为正整数），点B在线段AC上，在线段AC同侧作正方形ABMN及正方形BCEF，连接AM、ME、EA得到△AME.当AB=1时，△AME的面积记为S1；当AB=2时，△AME的面积记为S2；当AB=3时，△AME的面积记为S3；…；当AB=n时，△AME的面积记为Sn.当n≥2时，Sn-Sn-1=______.

解析：设正方形ABMN的边长为m，则CE=BC=ACAB=n+1-m.

点评：本题以“共顶正方形”为模型，以规律探索的形式考查了图形面积的求法.设出正方形ABMN的边长，并以正方形ABMN的边长表示梯形BCEM、△ABM、△ACE等特殊图形的面积是解决问题的关键，最后用这些特殊图形的面积来表示△AME的面积.从求解过程可以看出，阴影部分的面积只与△ABM的面积有关，即与正方形ABMN的边长有关，本题所用的解题方法与例1基本相同.

2.以“共顶正方形”为模型，判断角的大小关系

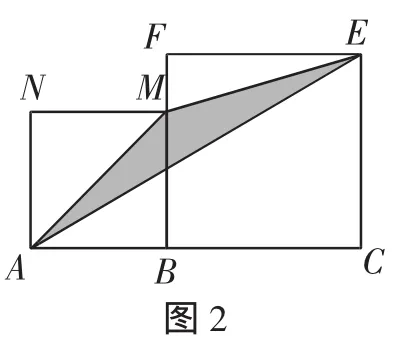
例3（2013年台湾省）如图3，四边形ABCD、AEFG均为正方形，其中E在BC上，且B、E两点不重合，并连接BG.根据图中标示的角，有下列关于∠1、∠2、∠3、∠4的大小关系的判断，其中正确的是（ ）.

A.∠1＜∠2 B.∠1＞∠2

C.∠3＜∠4 D.∠3＞∠4

解析：因为四边形ABCD、AEFG均为正方形，所以∠BAD=∠EAG=90°.

因为∠BAD=∠1+∠DAE=90°，∠EAG=∠2+∠DAE=90°，所以∠1=∠2.

因为△ABE是直角三角形，所以AE＞AB.

因为四边形AEFG是正方形，所以AE=AG.

所以AG＞AB，所以∠3＞∠4.故选D.

点评：本题以“共顶正方形”为模型，主要考查正方形的性质：正方形的四条边都相等，每一个角都是直角；同角的余角相等；在同一个三角形中，较长的边所对的角大于较短的边所对的角.在解题过程中将边的大小关系转化为角之间的大小关系是解决问题的关键.

3.以“共顶正方形”为模型，考查综合运用所学知识推理论证的能力

这类试题以“共顶正方形”为模型，涉及的知识点有线段的相等关系或位置关系、角的相等关系、全等三角形的性质和判定、正方形的性质、勾股定理等，突出数学知识的整体性，主要考查综合运用所学知识推理论证的能力.

例4（2013年辽宁营口）如图4，△ABC为等腰直角三角形∠ACB=90°，F是AC边上的一个动点（点F与A、C不重合），以CF为一边在等腰直角三角形外作正方形CDEF连接BF、AD.

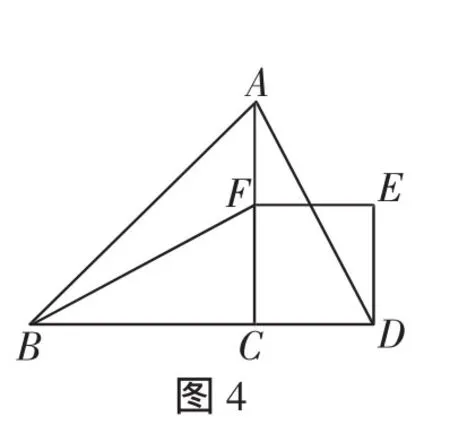
（1）①猜想图4中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论.

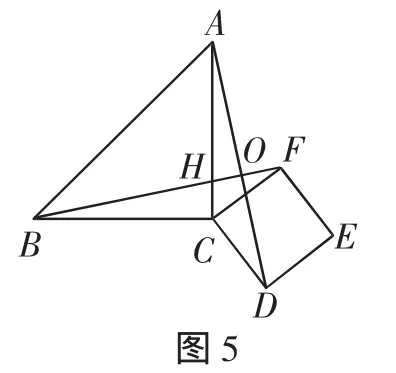
②将图4中的正方形CDEF绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图5、图6所示的情形.图5中BF交AC于点H，交AD于点O，请你判断①中得到的结论是否仍然成立，并选取图5证明你的判断.

（2）将原题中的等腰直角三角形ABC改为直角三角形ABC，∠ACB=90°，正方形CDEF改为矩形CDEF，如图7，且AC=4，BC=3，CD=，CF=1，BF交AC于点H，交AD于点O，连接BD、AF，求BD2+AF2的值.

解析：（1）①BF=AD，BF⊥AD.

②BF=AD，BF⊥AD.理由如下.

因为△ABC是等腰直角三角形，∠ACB=90°，所以AC=BC.

因为四边形CDEF是正方形，所以CD=CF，∠FCD=90°，所以∠ACB+∠ACF=∠FCD+∠ACF，即∠BCF=∠ACD.

（2）如图7，连接DF.

因为四边形CDEF是矩形，所以∠FCD=90°.

又因为∠ACB=90°，所以∠ACB=∠FCD，所以∠ACB+∠ACF=∠FCD+∠ACF，即∠BCF=∠ACD.

点评：本题第一问以一个等腰直角三角形和一个正方形为基本图形，主要考查等腰直角三角形的性质、正方形的性质、全等三角形的性质和判定等知识，这个基本图形其实还是“共顶正方形”，因为等腰直角三角形可补全为正方形.第二问中将等腰直角三角形ABC改为直角三角形ABC，将正方形CDEF改为矩形CDEF，使图形更具一般性，考查的知识点也由全等三角形转移到了相似三角形，在求值过程中还用到了勾股定理.本题改编之后更加具有挑战性，对学生来说具有一定的难度，也体现了中考的选拔功能.

三、以“共顶正方形”为模型的中考试题的变式探究

正方形是最常见的平面图形之一，它的性质学生非常熟悉.以正方形为基本图形组成的“共顶正方形”图形优美、内涵丰富，它在命题中具有广阔的变化空间.通过对以“共顶正方形”为模型的中考试题进行合理改编，或借助于几何画板的测量功能与超级画板的自动推理功能，可根据考查的目标和重点编拟一些形式优美的几何试题.

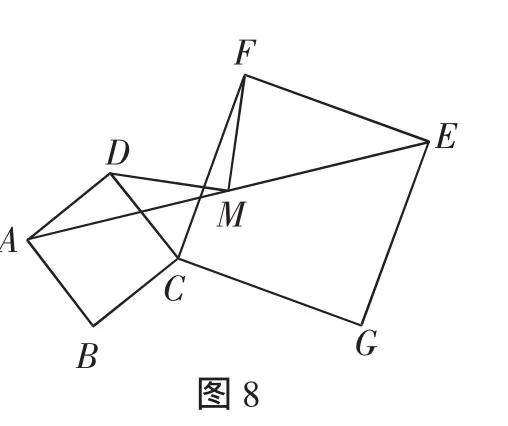
例5 如图8，正方形ABCD和CGEF是共顶正方形，连接AE，点M是线段AE的中点，连接DM、FM.求证：FM⊥MD，FM=MD.

证明：如图9，延长DM到点N，使MN=DM，连接DF、FN、NE.

因为M是线段AE的中点，所以AM=ME.

又因为∠AMD=∠EMN，DM=MN，所以△AMD≌△EMN.

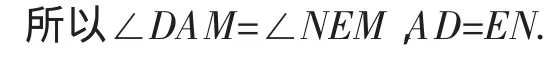
所以AD与EN平行且相等.

所以△CDF与△ENF中有两对边相等且垂直.

所以△CDF逆时针旋转90°后可以得到△ENF.

故△FDN是等腰直角三角形.

又因为点M是线段AE的中点，所以FM⊥MD，FM=MD.

说明：本题主要考查正方形的性质、全等三角形的性质与判定、直角三角形的性质，根据已知构造辅助线是解决本题的关键.

对图9稍作变化，可得到例6.

例6 如图10，在△BEF中，∠BEF=90°，BE=EF， 四 边 形ABCD是正方形，连接DF，G为DF的中点，连接EG、CG.

求证：EG=CG，EG⊥CG.

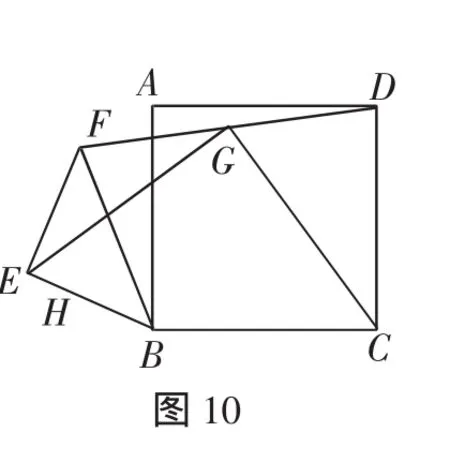
证明：如图11，延长CG至M，使MG=CG，连接MF、ME、EC，延长MF交CB的延长线于点N，MN交BE于点H.

在△DCG和△FMG中，FG=DG，∠MGF=∠CGD，MG=CG，所以△DCG≌△FMG.

所以MF=CD，∠FMG=∠DCG.所以MF∥CD.

因为四边形ABCD是正方形，所以∠DCB=90°，CD=BC.所以∠HNB=90°，MF=BC.

因为∠BHN=∠FHE，∠BEF=∠HNB=90°，所以∠EFH=∠NBH.

因为∠CBE＋∠NBH=180°，∠EFH＋∠MFE=180°，所以∠MFE=∠CBE.

在△MFE和△CBE中，MF=CB，∠MFE=∠CBE，EF=BE，所以△MFE≌△CBE.

所以∠MEF=∠CEB，EM=EC.

所以∠MEC=∠MEF＋∠FEC=∠CEB＋∠CEF=∠BEF=90°.

所以△MEC为直角三角形.

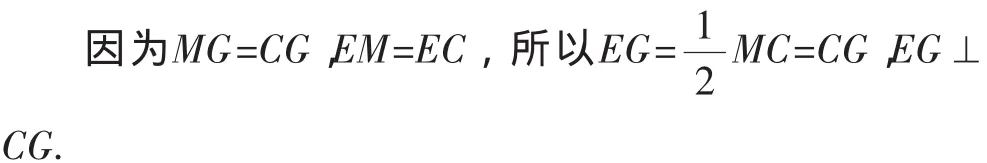
四、结束语

以“共顶正方形”为模型可以编拟出很多有趣的几何问题，这些几何问题表面上有所不同，但它们所蕴含的解题思想是统一的，解决问题的方法是类似的，只要抓住“共顶正方形”基本图形的特征，综合运用三角形全等、勾股定理、正方形的性质、三角形相似等相关知识进行探索，不难得出结论.通过这样的探究活动，不但可以为学生提供很多富有挑战性和探索性的学习素材，激发学生学习数学的兴趣，培养学生的发散思维和创新思维，有助于学生初步形成模型思想，提高学生的数学应用意识，而且对教师数学素养的提升也有一定的作用.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.张宁.以勾股图为模型的中考试题及其变式探究［J］.中学数学（下），2013（1）.

3.张宁.关注“直L形”图形模型 重视通法的解题功能［J］.中学数学（下），2013（8）.