一题激起千层浪 万流归宗能力成——对充分挖掘题目教学功能的案例剖析与反思

☉浙江省绍兴市建功中学 曹 青

一题激起千层浪 万流归宗能力成
——对充分挖掘题目教学功能的案例剖析与反思

☉浙江省绍兴市建功中学 曹 青

《全日制义务教育数学课程标准（2011年版）》强调四基四能（四基，即基础知识、基本技能、基本思想和基本活动经验；四能，即发现问题、提出问题、分析问题和解决问题的能力），关注学生的学习兴趣与习惯，倡导创新型和应用型人才的培养.要实现这些目标，离不开过程与方法教学，没有充分展开问题教学的时间和空间是不行的，在中考系统复习阶段时间紧任务重的情况下更是如此.本文深入分析一例，从中获得教学启示.

一、教学案例

出于问题引领系统复习教学的考虑，在充分研究的基础上，我们设计了一节以一题多解为特征的几何复习课，达到了良好效果.

问题：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.

首先把问题符号化：已知，如图1所示，在Rt△ABC中，∠ACB=90°，∠BAC=30°.求证：BC=AB.

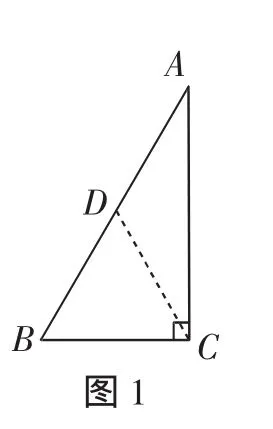
在学生眼里，此定理应用广泛，早已了然于胸.中考复习时施以“多证”，学生们切入容易，方法众多，堪称“一题激起千层浪”.由之理顺解题规律，水到渠成，自然流畅.

（一）截长补短法

顾名思义，“截长法”即在长线段上截下一段，使之等于短线段的方法；“补短法”则是在短线段上补上一段，使之等于长线段的方法.如此，往往能把分散的条件给集中起来，迅速释放题目内涵.

1.截长法

解法1：如图1，取AB的中点D，连接CD.结合∠ACB=90°，利用“直角三角形斜边上的中线等于斜边的一半”，可得CD=AD=BD=AB.又∠B=60°，则△BCD是等边三角形，于是有BC=BD=AB.

异曲同工之法，还有（只提供辅助线，不赘详解）：

方法变式1-1：在AB上取一点D，使BD=BC，连接CD.

方法变式1-2：作BC的中垂线交AB于点D，连接CD.

方法变式1-3：以点C为圆心、CB长为半径作圆弧，交AB于点D，连接CD.

方法变式1-4：在AB上取一点D，使∠BCD=60°.

方法变式1-5：作AC的中垂线交AB于点D，连接CD.

方法变式1-6：在AB上取一点D，使∠ACD=30°，连接CD.

2.补短法

方法变式2-2：作AB的中垂线交BC的延长线于点D，连接AD.

点评：遇到线段（角）的和、差、倍、分问题，采用截长（大）补短（小）的策略往往能释放题、图信息内涵，打开思路.

（二）线段叠合法

把一条线段叠合到另一条线段上去，让它们的一端重合，观察另一端的情况，就可比较两条线段的长短，同样也是判断和证明线段大小关系的常用策略.

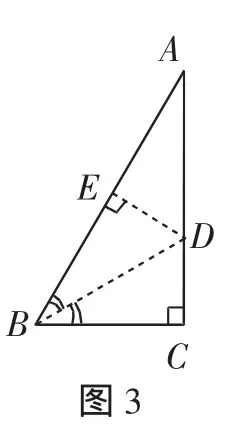
解法3：如图3，作∠B的平分线，交AC于点D，过点D作DE⊥AB，垂足为E.容易证明图中分出的三个小三角形全等，从而使问题获解.异曲同工之法，还有（只提供辅助线，不赘详解）：方法变式3-1：作AB的中垂线ED，交AC于点D，连接BD.

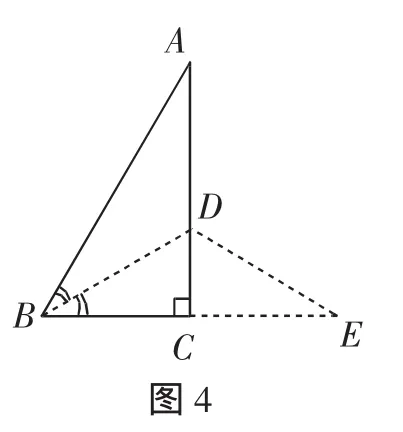
方法变式3-2：如图4，作∠B的平分线，交AC于点D，延长BC到点E，使BE=BA，连接DE.

方法变式3-3：作∠B的平分线，交AC于点D，以D为圆心、DB为半径作圆弧，交BC的延长线于点E.

点评：关注到两个锐角内在的数量关系和图形特征，结合待证目标，容易联想到借助角平分线巧妙完成线段叠合.角是以其平分线所在直线为对称轴的轴对称图形，我们常利用这一点把一侧的图形翻折到另一侧去，或无中生有——过角平分线上的上点向角的两边引垂线——完善图形成轴对称图形，同时一举多得，打开解证思路.

（三）“同一”证明法

当命题的条件与结论所指的事件是唯一的，且范围相同，则原命题的逆命题一定成立.这时若证明原命题不易入手，可改证其逆命题，是一种间接证法，我们称之为“同一法”.

运用“同一法”，一般经历如下步骤：

（1）作一个具有命题所述属性的图形；

（2）证明这个图形与已知条件符合；

（3）通过推理，说明所作图形与题设要求的图形是一致的；

（4）判断原命题所述图形具有某种属性.

解法4：如图5，延长CB到D，使BD=BC，以BD为一边作等边△BDE，连接CE，则DE=CD.又容易证明△CED≌△ACB，则有BC=AB.

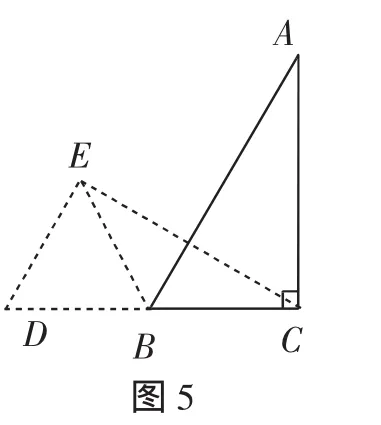
点评：从本质上说，这个办法与前述“截长”各法是相通的，但从思路上却各有千秋.本法突出在先构造符合目标条件的图形，再证明它与原图形全等；而“截长法”则指向探究对象的变更，如解法1中，由判断BC=AB转为判断BC=BD.

（四）相似推理法

全等是特殊（相似比为1∶1）的相似，相似是全等的深化.判定图形全等离开等线段是不行的，而判定相似则不然.因此，运用相似这个解证工具往往更加方便.

解法5：如图6，作∠ABC的平分线，交AC于点D.

点评：利用相似，一个典型的几何问题最终被化归为解一个代数方程.虽然在方程解法上，需要分组分解因式的方法，技巧性比较强，却不需要特殊的构图技巧，对几何思考的能力放低了一些.

二、教学启示

一题多解有利于加深对概念、命题的认识和理解，沟通数学各分支内容间的联系，以点带面地复习章节知识，找到最优解证思路，可以激发学习兴趣，促进探究学风的形成，是常用且有效的教学策略.

那么，上述案例达到这些目的了吗？能给我们一些什么教学启示呢？

（一）推陈出新，充分挖掘经典题目的教学功能

经典或说好的数学问题不一定是繁难问题，它应该是知识的交汇平台，有众多的思维切入点，能承载更多的思想方法成分.本例系教材定理，学生们熟能成诵，但上述处理却似枯树生新芽，各种方法均给人以新鲜之感，教学上主要体现为以下三点：

1.舍简求繁，只为领悟方法

教材是在学习完等边三角形以后，借助其对称性，观察局部与整体（命题对应三角形是等边三角形的一半）关系的基础上，以推论的形式自然引入该定理的，堪谓水到渠成.如果单从理解和证明命题考虑的话，显然毫无再度研究的必要.此处舍简求繁，在中考系统复习阶段又深入解读，目的只为在过程中感悟思想，提炼方法，积累数学活动经验.

2.颠覆经典，体味数学魅力

数学是思维的艺术.上述问题的解决一改传统思路，另辟蹊径，颠覆经典解法，展示了数学“道无止境，思有路径”的无穷魅力.当然，上述各思路并非全部生成于课堂，也并非完全生成于学生，其中有教师充分的研究、预设、点拨与启发，有学生开放的探索、合作、尝试与顿悟，更有师生间相互的“灵犀一动”！

3.承载思想，升华思维品质

经典问题必然能承载更多的思想方法，能建立并强化学生的数学意识，升华学生的数学观念，让学生“数学地思考”的能力不断提高.实际上，在本教学结束时，我们布置了一份作业，即证明上述命题的逆命题.二者的结合，不仅实现了方法的类比和迁移，更对截长补短法、线段叠合法、同一证明法、相似推理法做了再次极佳的诠释.不知不觉中，思维品质得到了升华.

（二）以点带面，充分感悟零散知识的内在联系

数学是一个有机的整体，各部分内容之间有着千丝万缕的联系.如何发现和感受这些联系，梳理知识网络，构建知识系统，以便在应用时“牵一发而动全身”，顺利提取和应用知识，释放题目内涵，是数学教学的追求.可从以下两点考虑：

1.经纬分明，手提金线串珍珠

学习数学的过程犹如编织一张渔网的过程.网面越大，则一网下去，即可覆盖更大的范围，获取更多的捕鱼机会；网眼越细，则大小鱼儿皆入网中；经纬线越粗，则网越发牢固.将之迁移到数学学习中，一张经纬分明、系统清晰的知识大网自然有助于信息的提取和应用.反映到教学设计中，教师首先要找到合适的数学问题，提炼引导学生学习的思维（或问题）线索，并以之串联起散落满地的数学珍珠——章节知识或数学不同领域的知识.

2.源流清晰，理顺脉络成网络

数学知识之间不仅存在以并列为特征的经纬分明的横向联系，更存在着先与后、主与次、源与流这些纵向的辩证联系.可以想象，要提起一大串葡萄，比较理想的办法是抓住果蒂.理顺出数学知识间的源流关系，则数学就可以成为一种结构，如因果、相关、相似、对比、相近等可实现相互推理的结构，以减少记忆量，更加容易联想.如解法1中，是线段的倍与分让我们联想到了截长补短；解法2中，把分散的两条线段集中到一条线上，容易发现图形的内在联系；解法3中，则先构造“理想目标”，再将之嫁接到原图形上；解法4中，则是发现并开发了两个锐角的内在数量关系，从而联想到构造角平分线，找到一对相似三角形.多种方法的实践与感悟，让学生们深入领会了作图、全等、相似、勾股定理、等腰三角形性质等诸多数学知识.一方面是从源到流的发散与分类，另一方面是从流到源的收敛与概括，二者的结合让数学在纵向发展上脉络清楚.

如上般组织教学，对教师的专业素养和研究能力是个挑战，而且教学可能显得费时费力，但其价值却是毋庸置疑的，实现了笨中取巧.望各位同仁再行深究，推广应用，服务教学，再入佳境.

1.王义堂.新课程理念与教学策略［M］.北京：中国言实出版社，2003.

2.陈明华.数学教学实施指南·初中卷［M］.武汉：华中师范大学出版社，2003.

3.苑建广.信息转化——问题解决的核心策略［J］.中国数学教育（初中版），2012（3）.

4.苑建广.激趣引思 移情启智——例谈教学内容的组织和引入［J］.中学数学（下），2012（9）.FH