破题策略：特殊直角三角形意识——由2013年河北省中考数学卷第26题说起

☉河北省唐山市路南区中学教研室 李姝侠

破题策略：特殊直角三角形意识
——由2013年河北省中考数学卷第26题说起

☉河北省唐山市路南区中学教研室 李姝侠

一、2013年河北省中考卷第26题的思路突破

例1（2013年河北中考第26题，有删减）一透明的敞口正方体容器ABCD－A′B′C′D′装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α（∠CBE=α，如图1所示）.

图1

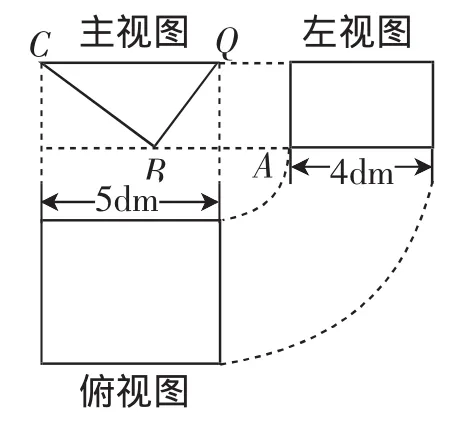
图2

探究 如图1，液面刚好过棱CD，并与棱BB′交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示.解决下列问题.

（1）CQ与BE的位置关系是___________，BQ的长是____________dm.

（2）求液体的体积.（参考算法：直棱柱体积V液=底面积SBCQ×高AB）

（4）在图1的基础上，以棱AB为轴将容器向左或向右旋转，但不能使液体溢出，图3或图4是其正面示意图.若液面与棱C′C或CB交于点P，设PC=x，BQ=y.分别就图3和图4求y与x的函数关系式，并写出相应的α的范围.

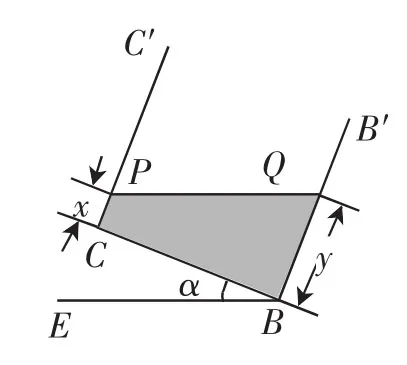
图3

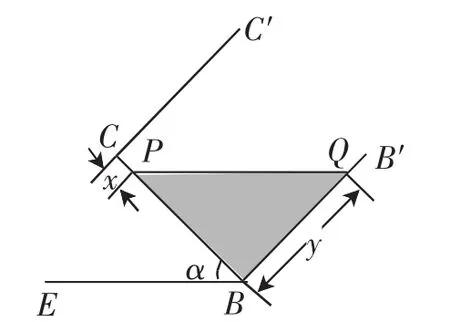
图4

思路突破：

（1）由常识知道CQ与水平桌面是平行的.

根据所给的三视图，有CQ=5，CB=4，于是由勾股定理易知BQ=3（注意：这是一个“3，4，5”的特殊直角三角形）.

（2）此时的液体形状是三棱柱，体积用底面积（Rt△BCQ的面积）与高BA（正方体的棱长）相乘即可得.

（4）分两种情况考虑.

当容器向左旋转时，如图3，此时0°≤α<37°.由于液体体积不变，此时底面图形由上一问中的三角形变成截面为梯形，可以用含x、y的式子表示底面积：1 2（x+y）·4，接着根据体积为24，可得关于x、y的等式，从而y与x的函数关系可获得.

当容器向右旋转时，如图4，此时α≥37°，但是上限不容易确定，需要考虑Q与B′重合的临界情况（如图5）.利用液体体积公式，有（4－x）y·4=24，变形得y=.由刚刚分析“Q与B′重合”，

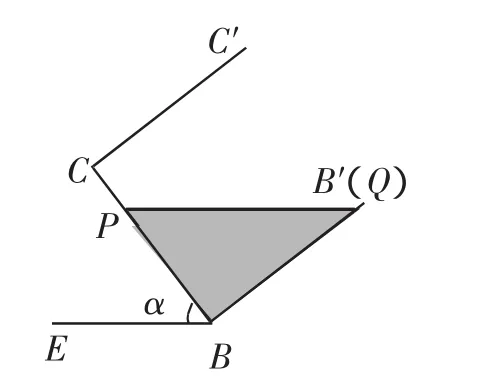
图5

即y=4时，x=1，BP=3. 此时在Rt△BPQ中，tan∠BQP=，得∠BQP=37°.相应的α=53°.于是37°≤α≤53°.

解后反思：想起了中国绘画艺术，讲究“三远”，即：平远、高远、深远.这就相当于“角度”和“透视”的道理.但又与西洋的透视学不同.后者总是以一个固定的“立足点”为本，还要寻求科学的“焦距”，然后方能展示全画面.中国则不然，是采用“分散立足点与焦点”的特殊表现法则.我们还想到了“一架高性能的摄像机”，可以发现上面图1~图5，都需要发现、构造、识别、切换、利用特殊直角三角形（有三边比为3∶4∶5，有含30°的直角三角形），能否选准这些特殊直角三角形，对思路的获取有很大的帮助.

根据笔者多年解题教学的经验，学生对这类问题的求解障碍往往是没有用好“特殊直角三角形”，或者说缺少“特殊直角三角形”意识，导致解题思路指向不精准，思路混乱，推证无力，下面再选编两道2013年中考题讲解思路，解后反思.

二、利用“含30°的直角三角形”意识解题

例2 （2013年江苏宿迁第26题） 如图6，在△ABC中∠ABC=90°，边AC的垂直平分线交BC于点D，交AC于点E，连接BE.

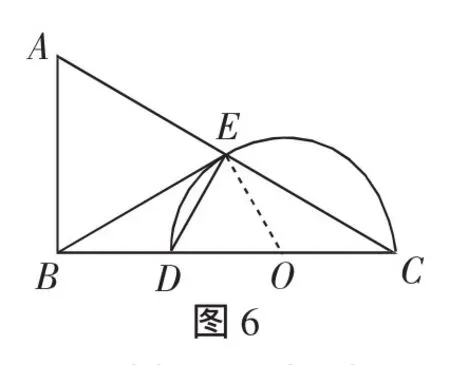
（1）若∠C=30°，求证：BE是△DEC外接圆的切线；

思路讲解：（1）受条件“∠C=30°”的启发，发现图6中应该有“含30°的特殊直角三角形”，如Rt△ABC、Rt△CDE.于是取CD的中点O，连接OE.

于是∠A=∠ABE=90°-∠C=90°-30°=60°.

由OE=OC，得∠OEC=∠C=30°.

进一步∠BEO=180°-∠AEB-∠OEC=90°，即BE⊥OE.

结合OE为⊙O的半径，所以BE是△DEC外接圆的切线.

解后反思：这道考题并不是一道太难的题，如果考生有特殊直角三角形的意识，能快速贯通思路，为惜时如金的考场应试带来时间上的效益.

对于上面的例2来说，有特殊直角三角形意识还只是思路获取上的快慢，对于下面的例3，如果有特殊直角三角形意识，则容易破解难题，获取突破方向.

例3（2013年四川成都第27题，有删减）如图7，⊙O的半径r=25，四边形ABCD内接于⊙O，对角线AC⊥BD于点H，P为CA的延长线上一点，且∠PDA=∠ABD.

（1）试判断PD与⊙O的位置关系，并说明理由；

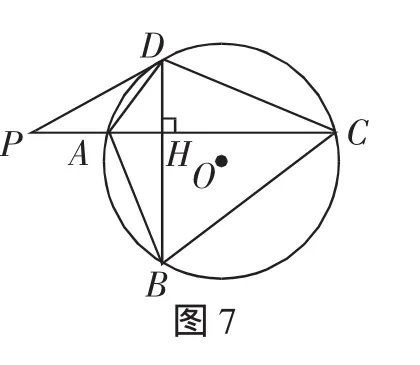
思路讲解：（1）PD与⊙O相切.理由如下.

如图8，过点D作直径DE，连接AE.则∠DAE=90°，即∠AED+∠ADE=90°. 由∠ABD=∠AED，∠PDA=∠ABD，得∠PDA=∠AED.所以∠PDA+∠ADE=90°.所以PD与⊙O相切.

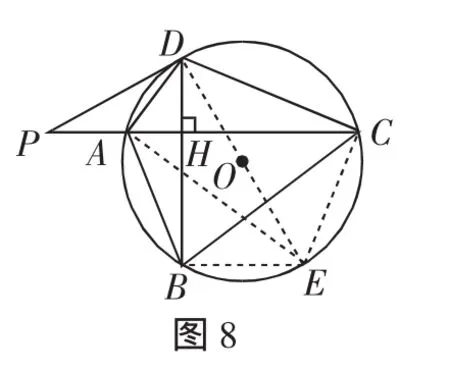
解后反思：可以发现，第二问的求解需要对两种不同的特殊直角三角形保持敏锐的识别能力，并且需要灵活切换、充分利用，这样才能在复杂图形中解决问题.

三、“特殊直角三角形意识”的破题意义

1.解题教学中教会学生学会审题，对强化条件保持足够的敏感

数学解题一般都是由已知出发，向待求（待证）方向前行，在这个过程中，难题之难往往在于当无法顺利前进时，需要退回题目，仔细看条件，特别是分析强化条件可能带来什么信息，甚至某一个强化条件的价值能否被充分的发挥，这是很关键的.正如波利亚在名著《怎样解题》［1］的“一段对话”下反复问“我应该从哪儿开始？”.本文倡导关注“特殊直角三角形意识”，就是倡导在解题教学中教会学生学会审题，特别是对强化条件保持足够的敏感.像例3第二问中，如果对“tan∠ADB=”不够敏感，往往就不能很快想到“设AH=3k，有DH=4k，AD=5k”，而这将影响难题破解、思路打开的快慢.

2.引导学生思辨特殊与一般的关系，促进对模式识别策略的理解

解题教学中，启发学生由特殊条件发现、识别、构造、充分利用特殊图形（包括本文提出的“特殊直角三角形”），其实也是引导学生思辨特殊与一般的关系.往大了说，数学教学就是在一般和特殊中不断地切换，有时需要在一般中发现特殊，有时又要由特殊走向一般.顺便提及，罗增儒教授在《解题学引论》中指出：“学习数学的过程中，所积累的知识经验经过加工，会得出有长久保存价值或基本重要性的典型结构与重要类型——模式，将其有意识地记忆下来.当遇到一个新问题时，我们辨认它属于哪一类基本模式，联想起一个已解决的问题，以此为索引，在记忆贮存中提取出相应的方法来加以解决，这就是模式识别的解题策略.”可以发现，本文倡导的关注“特殊直角三角形”意识，其本质也是引导学生重视模式图形的发现、积累与利用，只是换了一种理解的方式，从不同的角度促进学生学会解题，提高解题能力.往大了说，这也是一种变式教学、多元表征式的教学.

1.［美］波利亚.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.

2.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.