培养学生数学探索能力的几点思考

☉江苏省南通市八一中学 徐菊华

培养学生数学探索能力的几点思考

☉江苏省南通市八一中学 徐菊华

一、前言

创新能力教学，是新课程改革以来中学教育提出的重要改革方向.以往传统中学教育，培养了大量的基础扎实、操作熟练的学生，但是在更高层面的教育中，学生往往创新精神不足.这非常像20世纪60年代美国提出的“大众教育”与“精英教育”如何合理对待，合理发展.

创新来源于什么呢？对初中学生而言，比较贴合创新的又是什么呢？笔者认为，想要从形式化的数学科中去得到创新既不简单也并非很难！之所以说简单：其一，数学要创新，必然经历探索这样的环节，要学会自我探索、合作探索，培养探索能力是第一步；其二，把握方向，从教材中去寻找值得挖掘的素材，可以是问题的提升，也可以是课后阅读，也可以是课外读物等；其三，通过探索增加兴趣，进而培养学习的能力才是关键.之所以说难：因为平时教师和学生往往受作业、应试等限制，没有时间去进行探索，更谈不上创新；另一方面，大量的枯燥重复训练，使得学生早已对数学丧失兴趣，进而谈何探索？

所以，笔者建议我们要放开一些胸怀，不要让解题成为初中数学教育的全部.在允许的范围内，教师积极开创条件，引导学生从多个角度去进行数学知识的探索，通过探索培养其数学学习的能力，进而为长远的创新能力的培养打下一定的基础.本文将结合教学实践，从多个角度浅谈探索能力的培养方式和手段，请读者指正.

二、探索能力的培养方式

探索能力是一种以一定基础为本，通过分析新型问题并利用部分已知知识解决未知问题，在解决问题的过程中，有时出现各种变化，需要学生不断调整知识方向进而解决问题的能力.笔者结合案例，谈谈具体的一些实施.

1.以双基知识为载体的问题探索能力

案例1：《探索三角形相似的条件》双基探索.

笔者本次教学过程设计的依据是：人类认识数学具有“渐进性”，个体对数学概念的认识要在不断地重复之中细化、深化以致内化.因此整体设计思路是围绕三角形相似产生的核心思想这个中心，在不同媒介的不断重演中，由浅入深将问题串抛给学生，层层推进学生对相似的判断、理解，以期达到增加学生解决类似问题经验的积累.教学实施环节如下所示.

（1）引入.

师：同学们记得三角形全等的判定定理吗？

生：有SSS、SAS、AAS三种常用方式.

师：是的！判断两个三角形全等并不需要三角相等，三边也相等，而只需具备特定的条件即可.那么两个三角形相似一定要具备三角对应相等、三边对应成比例的条件吗？符合特定条件的三角形是否可以相似呢？下面一起探究三角形相似的条件.

（2）探索.

（投影）（i）画一个△ABC，使得∠BAC=60°.所画的三角形相似吗？检查一下除了等于60°的角相等，还有其他相等的角吗？

（ii）请学生一人画△ABC，另一人画△A′B′C′，使得∠A和∠A′都等于给定的∠α，∠B和∠B′都等于给定的∠β.比较你们画的两个三角形，∠C与∠C′相等吗？对应边的比相等吗？这样的两个三角形相似吗？

结论：两角相等的两个三角形相似.

说明：探索性教学模式在设计理念上紧紧围绕着新课程的核心思想——学生对知识形成过程的追求，在教学实施中以学生为主体进行课堂设计，围绕教学过程中产生的实施、反馈、评价和反思，进行自主化的管理和学习，即重在知识形成过程的参与.

（3）能力.

（投影）例题：如图1，D、E分别是△ABC的边BA、CA的延长线上的点，DE∥BC.

①图中有哪些相等的角？

②找出图中的相似三角形，并说明理由.

③写出三组成比例的线段.

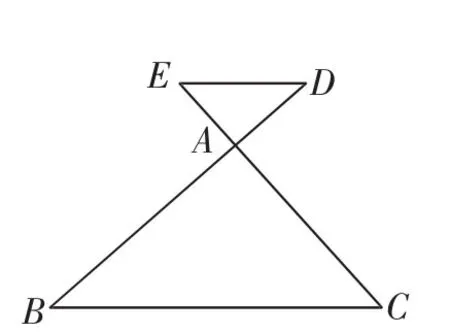
图1

变形1（PPT演示）：移动线段DE，使∠AED=∠B，回答上面的问题.

（PPT投影）①∠A=∠A，∠ADE=∠C；

②△ABC∽△AED.由∠B=∠AED，∠C=∠ADE，得△ABC∽△AED.

变形2（PPT演示）：继续移动线段DE，使E点与C点重合，并保持∠AED=∠B，回答上面的问题.把上面结论中的字母E改为C，结论仍然成立.其中AC2=AD·AB.（投影相关结论）

变形3（PPT演示）：特殊地，当AC⊥BC，CD⊥AB时，变为图2，回答上面的问题.对应点没有变，上述结论仍成立.但由于特殊性，这时还有△ABC∽△CBD，则△ABC∽△ACD∽△CBD.（投影相关结论）

说明：探索性能力学习将探究的难度层次进一步提升到知识运用的阶段，其主要目的是通过探索教学模式，使得学生深刻感受解决类似问题的经验积累，将知识运用至举一反三的地步，彻底解决学生双基知识在具体情境中的熟练运用.

2.以课外兴趣为载体的创新探索能力

笔者在介绍《不等关系》时，给竞赛班的学生提到过一个不等关系的性质：若a＞b，b＞c，则a＞c.竞赛班的学生比较容易接受不等式的传递性，有些学生对不等式的兴趣恰恰从这些关系式中得以培养.笔者以学生对不等式的兴趣，开发了带有兴趣性的不等式研究，旨在通过情境化的手段培养学生探索更多不等式的性质.

案例2：2011年3月11日，日本本州岛附近海域发生强震，现在对强震遗留下来的什么最担心？

核危机！核辐射主要存在三种射线：ALPHA（阿尔法）射线、BETA（贝塔）射线、GAMMA（伽玛）射线.我们不妨记ALPHA（阿尔法）粒子的质量为a，BETA（贝塔）粒子的质量为b，GAMMA（伽玛）粒子的质量为c，三者的质量关系是a＞b、b＞c.

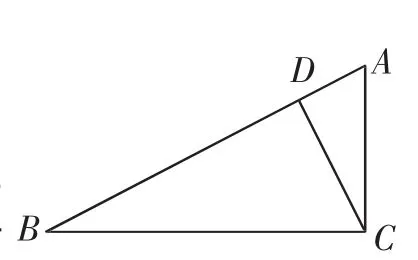
图2

（1）如果把前两种粒子放在天平的左、右两端上，由于a＞b，显然左端会下降；若我们将其交换位置，则右端会下降，于是我们得到性质1.

性质1：若a＞b，则b＜a.（对称性）

（2）由于三种粒子的的质量关系是a＞b、b＞c，得到性质2.

性质2：若a＞b，b＞c，则a＞c.（传递性）

（3）不妨在天平两端的ALPHA（阿尔法）粒子与BETA（贝塔）粒子上，各自加上一个GAMMA（伽玛）粒子，则天平平衡性保持不变，得到性质3.

性质3：若a＞b，则a+c＞b+c.（可加性）

（4）GAMMA（伽玛）粒子放射出能量衰变一次之后的质量变为d，且c＞d，那么在天平两端的ALPHA（阿尔法）粒子与BETA（贝塔）粒子上，分别加上一个GAMMA（伽玛）粒子和衰变后的GAMMA（伽玛）粒子，则天平平衡性显然保持不变，得到性质4.

性质4：若a＞b，c＞d，则a+c＞b+d.（同向不等式可加性）

（5）若取出m（m＞0）个ALPHA（阿尔法）粒子与BETA（贝塔）粒子，按类别放在天平两端，则显然ma＞mb，得到性质5.

性质5：若a＞b，c＞0，则ac＞bc；若a＞b，c＜0，则ac＜bc.（可乘性）

（6）若取出m个ALPHA（阿尔法）粒子与n个BETA（贝塔）粒子，且m＞n＞0，将其按类别放在天平两端，则显然ma＞nb，得到性质6.

性质6：若a＞b＞0，c＞d＞0，则ac＞bd.（同向正值不等式可乘性）

上述结论，我们只做了从特殊情形的考虑，有兴趣的同学可以对其进行严格证明，我们在课堂上不赘述，列表总结上述六条性质，学生对探索得到的不等式的性质极为有兴趣，记忆深刻.

3.以数学文化为载体的兴趣探索能力

文化往往对学生起着精神的引领作用，在介绍数字规律的时候，笔者提起了“高斯求和1+2+…+100”，课后有几个兴趣盎然的学生对问题进行了不断地探索和追求，笔者抽时间和学生一起做了一些探索和思考.

案例3：探索：（数与字母）

①已知数列2、4、6、8、10、…，第n项（n为正整数）是______，其和是______；

②已知数列1、6、11、16、21、…，第n项（n为正整数）是___，其和是___；

③已知数列2、3、5、8、12、…，第n项（n为正整数）是______，其和是______.

对于数列①，同学们不难发现这些数都是偶数，一切偶数总可以表示成2n的形式，所以第n项就是2n.关于其和的问题，给同学们几分钟时间后，就有同学发现答案.其和用S表示.

这位同学说得多好啊！是否还有其他算法？学生沉入思考.过了一段时间，学生想不出其他好的算法，笔者略作提示：此数列是按从小到大的顺序排列的，能否按从大到小的顺序排列，比较并加以思考.在笔者的提示下，有同学发现，回答.

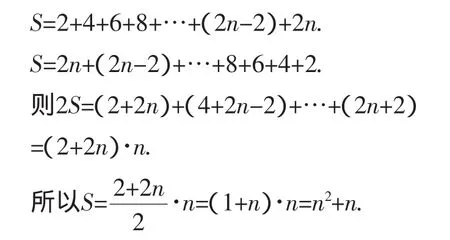
这位同学的回答着实让笔者兴奋.接着就问奇数列1、3、5、7、9、…呢？不到一分钟的时间，同学们的答案就有了，第n项为2n-1，其和为n2.

趁着同学们探究兴趣的来临，笔者就提出了数列②.经过分组讨论，发现相邻两项都相差5，故可以把此数列表示成：1、1+5×1、1+5×2、1+5×3、…、1+5（n－1），这时第n项就是1+5（n-1）=5n-4.

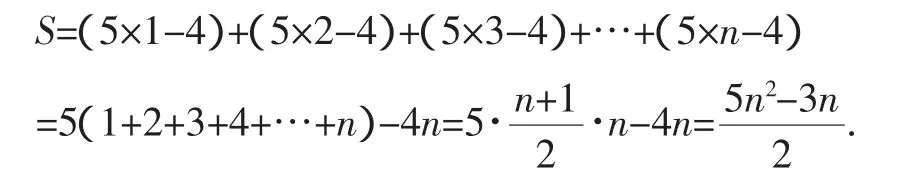
题目的难度在逐渐地增加，同学们探究的激情丝毫未减，笔者继续为其加油：“只要努力，高山也会变成坦途，数学会带给我们无限的乐趣.”这时笔者就鼓励他们继续观察数列③的特征.能发现什么呢？对数据进行剖析.

2=2，3=2+1，5=2+1+2，8=2+1+2+3，12=2+1+2+3+4，…，这样一提示，同学们就领悟到了数列的特征！那么第n项该怎样表示呢？就有同学举手发言：第n项应该是：

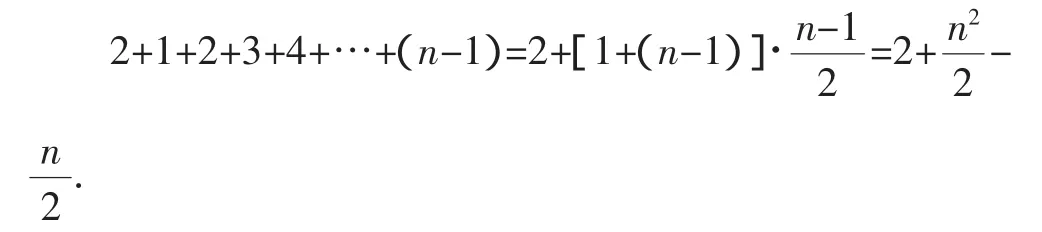
笔者又问：2008年我国将举办奥运会，若n=2008，这一项又是什么数据呢？这时同学们的计算器劈劈啪啪响个不停，答案一下子就出来了：2015030，那么其和呢？求和有一定的难度，解答如下.

三、结语

通过上述案例，笔者认为探索能力的培养应该以高于教材和中考应试问题为基准，在探索过程中也可以一起尝试或在教师指导下进行操作，问题主要靠教师准备，在培养过程中，需要体现下列基本原则.

1.适合性原则

给学生探索的问题需要有一定的适度性，既不能大部分学生都能解决，也不能所有学生完全摸不着头脑，给出的问题要符合“最近发展区”理论，使得优秀学生通过思考可以摸得着.

2.应用性原则

一般探索性问题往往是纯数学或数学与生活实际相结合的问题，无论何种问题，都体现了数学知识的应用性，使学生深刻理解所学的数学知识在解决未知问题时的作用.

3.兴趣性原则

数学本身是一门相对枯燥的学科，对探索能力的培养要选择一些有趣味的问题，尽量避免枯燥的纯数学的理论，这对初中学生而言是不合适的.

限于篇幅，笔者以案例实践对探索问题做了一些浅显的操作，并在操作中记录了一些心得，不足之处在所难免，恳请读者继续补充.

1.张奠宙.情真意切话数学［M］.北京：科学出版社，2010.

2.展国培.有效教学，从关注学生开始［J］.中小学数学（初中），2013（1）.

3.王俊.关于学习反思的几点思考［J］.中学数学（下），2003（1）.

·江苏省无锡市庞彦福名师工作室·