一道九年级期末原创题的命制过程与感悟
2014-02-01南京师范大学附属中学新城初中何君青
☉南京师范大学附属中学新城初中 何君青
一道九年级期末原创题的命制过程与感悟
☉南京师范大学附属中学新城初中 何君青
九年级第一学期期末学情分析考试是一次阶段性检测,其功能是评价学生一学期以来对知识的掌握情况,同时这类考试还承担了学生对中考适应性衔接的功能,所以这类考试无论学校还是学生都高度重视.笔者有幸命制了我区九年级期末学情分析考试试卷,考试结束后这份试卷得到了我区教师们的一致认可.
下面就此次考试中笔者命制的一道原创题的过程,谈谈有关命题的一些感受.
一、试题呈现
探究:
七年级我们学过三角形的相关知识,在动手实践的过程中,发现了一个基本事实:三角形的三条高(或三条高所在直线)相交于一点.
其实,有很多八年级、九年级的问题均可用此结论解决.
运用:
(1)如图1,已知△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.

图1
小方同学在解答此题时,利用了上述结论,她的方法如下:
连接CF并延长,交AB于点M.
因为△ABC的高AD与高BE相交于点F,所以CM为△ABC的高.
(请你在下面的空白处完成小方的证明过程)操作:
(2)如图2,AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.
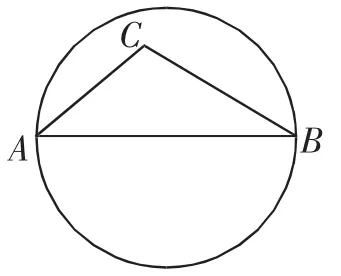
图2
分析:本题分值9分,第一问5分,第二问4分,试卷共27题,此题为第25题,难度适中,属于中档题.本题以七年级一个重要结论为背景,通过对此结论的深刻认识和理解进而解决两个九年级的问题,第一问主要考查几何证明,第二问主要考查圆的相关结论,这均为中考的必考知识点,同时也能考查类比思想、转化思想,兼顾基础性和区分度,能较好地体现出学生的数学水平.

(2)如图3.
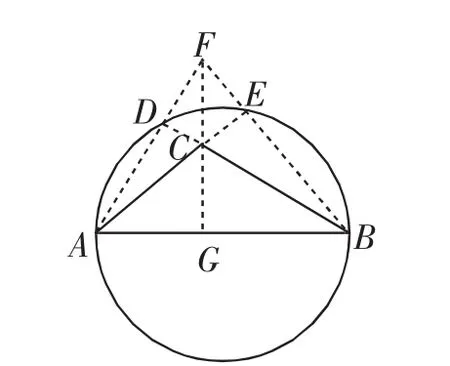
图3
二、命制过程
1.取材背景
试题的改编、创作离不开“题源”,而课本却是最好的“题源”地.一道好的试题应该“源于课本”而又“高于课本”.在找好“题源”后,应当确定改编的方向,沿某个角度深度挖掘,才能使得考题绽放光彩.
中考试题中的很多好题也是“生长”于课本中的某些结论和例题,此次期末考试的功能之一就是让学生感受中考,所以必须以中考命题的要求来作为此次期末命题的标准.笔者曾发表过一篇关于中考试题研究的文章,对南京近几年的中考试题略有研究,曾指明近几年南京市中考数学试卷总体平和,整体难度适中,试卷的命题思路基本保持一致,均重视数学最核心的“四基”:基础知识、基本技能、基本数学思想方法和基本活动经验的考查.另外,试卷有一些比较新颖的试题,更加公平、公正地评价学生,试题内容涉及“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”四个学习领域.知识点的考查既注意全面,又突出重点,注重知识内在联系的考查,注重对初中数学所蕴含的数学思想和方法的考查.结合《新课标》,笔者决定在试卷中命制一道阅读型数学问题,不仅能体现基础知识、基本知识的运用,更能通过学生的操作活动,体现数学的基本思想.
本着“根在书内,题在书外”这一理念,笔者翻阅苏科版教材,在七年级下学期课本中发现了这一结论:三角形的三条高(或三条高所在直线)相交于一点.这一结论学生虽然了解,但是运用极少.于是,笔者查阅历届中考试卷中的这类问题,均未涉及.
2.命题思想
新课标中明确指出:“数学在应用方面需要大力加强,鼓励学生发现数学的规律和问题解决的途径,使他们经历知识的形成过程.”创新型阅读试题是考查学生数学能力的最好题型之一,它是建立在已有知识的基础上,对考查学生的阅读理解能力、知识迁移能力、类比猜想能力、数学探究能力、数学创新意识等都有良好的作用,这类题型是“用数学”的直接体现.
如何将这个结论加以发展,使考题具有新颖性、创新性是笔者需要突破的关键.三角形的三条高(或三条高所在直线)相交于一点,这个结论显然应该在几何问题中加以发展,最容易想到的就是几何证明,很快地笔者编制了“结论运用”,又由于圆是中考几何问题中的必考点和难点,很快笔者联想到圆中的结论:在圆中,直径所对的圆周角是直角,于是“结论操作”应运而生.
在命题初稿时,值得肯定的是本题取材合理:立足基础知识、基本技能;角度新颖:着眼于几何证明和圆中的相关结论;题型丰富:既有证明又有画图.
3.商榷定稿
新课标明确提出对数学教学的目标要包含数学思考,原先的中考试题往往都是比较单一的试题,考查学生对知识的掌握情况,而近3年来,南京中考题中也出现了很多新颖性的创新题型,这类题体现了“不同的学生在数学上得到不同的发展”的理念,考查了学生的发散思维能力,让不同层次的学生都有展示的空间.为了达到这一目标,笔者将第一问难度适当降低,给出一半的解答过程,让学生完善下面的步骤,第二问提高难度,未给予学生明确的解答方向,有一定的难度.从试题的发展过程看,第一问运用结论:三角形的三条高交于一点,第二问运用结论:三角形的三条高所在直线交于一点,更让题目具有丰富性.
4.总结反思
这道题的命制新颖,有丰富的背景,以七年级的结论加以运用解决九年级的问题,贯穿初中3年,很具典型性,但笔者认为此题还能加以发展,若将该题再发展到代数领域,运用数形结合的思想解决更多的初中数学问题就更完美了,由于时间有限,未曾拓展,确实可惜.
三、命题感悟
衡量数学试题质量的高低,要看在符合考试性质的前提下,其试题立意的高低、基本价值立场、价值态度以及所表现出来的基本价值倾向和对教学的引导与促进作用,即试题的价值取向,一道高质量的试题,反映了命题者对课程改革精神的深度领悟、对数学本质的准确把握和对教学的高期待.对于教师的命题首先应以《新课标》为理念,再查阅多年中考试题,最后找到合适的“题源”,加以模仿,争取创新,这样才能命制出经典好题.
作为与中考衔接的大型区域性考试,导向教学是期末学情分析考试的重要功能.在当今教学实践中,普遍存在重教轻学、重训练轻思想、重结果轻过程、重技巧轻智慧的现象.这些教学中的负面价值取向严重遏制了学生数学的发展,所以通过考试试题的命制应当让教师清醒地认识到这点,故在教学时教师应让学生通过自己的思考,理解知识之间的相互联系,建立知识网络,重视对数学知识的理解和数学方法的感悟,重视大智慧.“以考导教”应当逐步让教师接受.
一道试题的产生过程应该经历:取材——初稿——修改——定稿——反思,试题完成后一定要对试题进行评价和反思,总结得失,积累经验,将好的部分加以发展,形成变式题,这也是我们常说的举一反三,同时对失败的地方认真总结,避免一错再错.
在深入推进课程改革的过程中,数学试题更要着眼于学生的发展,注重课程理念与现实结合、基础与能力并重,命题设计与构思充分挖掘考试的积极引导功能、激励功能和评价功能.虽然此题的命制已经结束,但若将此题再发展,说不定会有更为精妙的地方产生.FH
