引入符号表征,重视推理表达——以七年级“三角形的高、中线与角平分线”的教学为例
2014-02-01江苏省东海县安峰初级中学杨海宁
☉江苏省东海县安峰初级中学 杨海宁
引入符号表征,重视推理表达
——以七年级“三角形的高、中线与角平分线”的教学为例
☉江苏省东海县安峰初级中学 杨海宁
近读史宁中教授《数学思想概论》(第1~5辑)[1],享受于史教授对基本数学思想(抽象、推理、模型)的概括和阐释.特别是,作为第1~2辑讲述的重点,关于“抽象”,史教授特别指出了符号表达的重要意义,这引发笔者对新近在七年级执教“三角形的高、中线与角平分线”的思考,本文主要展示该课的教学设计、生成片断,并给出三点反思,与同行交流.
一、教学设计简案
(一)教学目标
1.经历折纸、画图等实践过程,认识三角形的高、中线与角平分线.
2.会用工具准确画出三角形的高、中线与角平分线,通过画图了解三角形的三条高(及所在直线)交于一点,三角形的三条中线、三条角平分线都交于一点.
3.通过学生作图、观察、比较、描述图形等数学活动,让学生感受数学的严谨性,图形中蕴含的规律性,提高学生学习数学的热情及大担探究新知识的创新能力.
(二)教学流程
1.阅读教材相关概念并对话交流.
2.师生合作整理三角形中三种重要线段,从概念、图形、符号语言的角度理解与掌握.
3.画图活动.
活动1:在练习本上画出三角形,并在这个三角形中画出它的三条高.
预设追问1:如果他们所画的是锐角三角形,接着提出直角三角形的三条高在哪里?钝角三角形的三条高在哪里?
预设追问2:观察这三条高所在直线的位置有何关系.
预设答案:三角形的三条高交于一点,锐角三角形三条高的交点在三角形内部,直角三角形三条高线的交点为三角形直角顶点,而钝角三角形三条高的交点在三角形的外部.
活动2:在练习本上画三角形,并在这个三角形中画出它的三条中线.
预设追问1:如果我们所画的是锐角三角形,接着我们画出直角三角形和钝角三角形,看看这些三角形的中线在哪里?
预设追问2:观察这三条中线的位置有何关系?三角形的一条中线把三角形的面积分成两个面积相等的三角形.
预设答案:三角形的三条中线都在三角形内部,它们交于一点,这个交点在三角形内部.
活动3:在练习本上画一个三角形,并在这个三角形中画出它的三条角平分线,观察这三条角平分线的位置有何关系?
预设答案:无论是锐角三角形还是直角三角形或钝角三角形,它们的三条角平分线都在三角形的内部,并且交于一点.
4.例题巩固.
例1 如图1,是甲、乙、丙、丁四位同学画的钝角△ABC的高BE,其中画错的是_________.
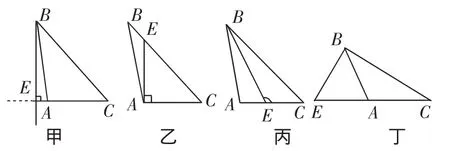
图1
预设意图:这是学生在解题时的一个易错点,通过例题强化理解画高时的两个注意点:一是过哪个点;二是垂直于哪条边.
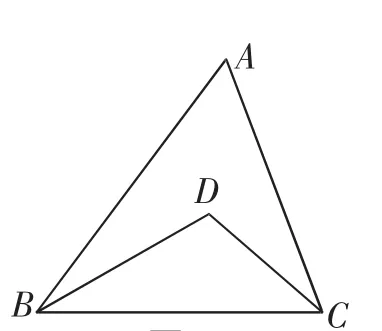
图2
例2 如图2,BD、CD分别平分∠ABC和∠ACB.
(1)若∠A=70°,求∠BDC的度数;
(2)试判断∠BDC与∠A的关系,并说明理由.
预设意图:这道题在三角形的角平分线问题中具有典型性,体现由特殊到一般的思想,本题是已知两条内角平分线,探索其夹角与第三个内角之间的关系,为后面研究一外角平分线与一内角平分线与第三个内角之间的关系,两外角平分线与第三个内角的关系作铺垫.
预设追问:通过以上求解发现了哪些规律?请总结且与同伴交流.
预设意图:第(1)、(2)题体现由特殊到一般的规律,即由已知∠A的度数求出∠BDC的度数,再由不告知∠A的度数,求出∠BDC与∠A的关系,体现内在规律.
5.练习巩固(略).
6.小结作业(略).
二、课堂生成片断
生成片断1:新知引入阶段.
师:同学们在小学阶段都学过了三角形的高,那么什么叫三角形的高?三角形的高与垂线有何区别和联系?
生1:(抢着站起来)三角形的高是从三角形的一个顶点向它对边所在的直线作垂线,是顶点和垂足之间的线段,而从三角形一个顶点向它对边所在的直线作垂线,这条垂线是直线.
师:什么叫三角形的中线?连接两点的线段与过两点的直线有何区别和联系?
生2:三角形的中线是连接一个顶点和它对边的中点的线段,而与过两点的直线有着本质的不同,一个代表的是线段,另一个却是直线.
师:什么叫三角形的角平分线?三角形的角平分线与角的平分线有何区别和联系?
生3:三角形的角平分线是三角形的一个内角平分线与它的对边相交,是这个角的顶点与交点之间的线段,而角的平分线指的是一条射线.
师:三角形的高、中线和角平分线是代表线段还是代表射线或直线?
集体回答:线段.
生4:三角形的高、中线和角平分线都是线段,这些线段的一个端点是三角形的一个顶点,另一个端点在这个顶点的对边上.
师:小学阶段学习三角形中这三种重要的线段时,我们往往凭着直觉可以直接进行相关的运算或解题,进入初中后,我们需要更加规范、简练地说理和表达,所以下面我们一起来整理下表(见表1).

表1:三角形的重要线段一览表
生成片断2:画图活动后的对话.
师:同学们都在三角形中画出了三角形的三条高了,看看三条高的位置有怎样的关系?
生5:我在小学里就知道,锐角三角形的三条高都在内部,交于一点.直角三角形两条高在边上,一条高在内部,且交于直角的顶点.钝角三角形两条高在外部,一条高在内部,且延长线交于一点.
师:总结得很好!
师:再看不同的三角形三条中线的位置有何特点?
生6:三角形的三条中线都在三角形内部,且它们交于一点,这个交点在三角形内部.
师:三角形的一条中线把三角形的面积怎样了?
生7:平分(等底同高).
师:继续思考,不同三角形中三条角平分线的位置关系如何?
生:锐角三角形或直角三角形或钝角三角形,它们的三条角平分线都在三角形内,并且交于一点.
师:很好!完全正确.如果把它们恰好交于一点称为数学的奇异性的话,随着我们学习的深入,以后我们还会研究、解释并证明这种奇异现象.
三、教学反思
(一)引入符号表征,渗透多元表征
日本数学家米山国藏在总结数学的两大特征时,曾指出:“为了有助于‘人类思想表达的经济化’(这里的经济化是指变得简洁,省事),数学使用了比其他任何科学都要多得多的术语和记号.”[2]米山认为:“若不用这些数学术语来表达相似的意义,而要用普通的语言来完整地表达它,那就一定会变得冗长复杂难于理解,其内容也一定混淆不清.用简洁的文字表达具有复杂内容的事物或关系的同时,还采用简单的记号来表示它们,如≌或∽符号.”事实上,这也正是中小学数学的一个重要不同,相对于小学数学来说,初中阶段的数学符号语言更加丰富、简洁,上文课例中,在“生成片断1”师生一起整理“表1”,其中特别小结出了符号语言表示,就是要引导学生重视符号语言的表达.此外,“表1”中还体现了对于同一概念的不同表征,也即当前受到重视的“多元表征”理论,就是指“人们关于数学概念(或数学问题)的心理表征往往包含多个不同的方面或成分,而且这些成分对于概念的正确理解都具有重要的作用,我们应高度重视这些成分之间的联系.”[3]
(二)重视推理表达,从直观到理性
初中阶段是学生系统学习欧氏平面几何的开始,是学生在图形学习时以直观、直觉、猜想、合情推理为主逐渐转向理性、说理、证明、思辨.初中几何系统学习点、线、三角形、四边形、圆、图形变换等内容,应该指出,欧几里德在《几何原本》中给出五个公设[4]与五个公理,即是以此出发,演绎推理出“一座大厦”,当下初中数学多种教材中给出的公理、定理、推论,都是基于“五个公设”、“五个公理”演绎出来.这样来看,从七年级开始,像上文提及的三角形中重要线段的课例中,不满足于简单的性质再现,而是重视符号语言、简单推理表达,就是追求从直观到理性的过程.此外,上文“生成片断”的教学对话中,涉及教师对学生的有效追问,这里也可提及日本著名教育学者佐滕学的观点:“教师的关键不在于说而在于听.我也认识到当今世界很多优秀的教师,大家都认为教师的工作重心是倾听.对学生来讲同样如此,只有更好地倾听,才能达到更好的学习效果.我们需要明确的是‘互相学习’和‘互相说’是完全不同的两件事.”[5]显然,课堂教学中的互相倾听需要教师的耐心,而不是急着打断、帮助优化.
(三)注意中小衔接,思辨解题表达
美国教育心理学家戴维·奥苏贝尔曾说:“影响学习的最重要的因素是学生已经知道了什么,要根据学生的原有知识状况进行教学.”所以在上文的教学设计和教学对话中,能看到中小学之间的衔接,无论是教师的教学设计,还是学生在回答问题时提及的“小学里就已经知道”,说明重视中小学衔接是十分重要的.在这里,需要提及,当前有些初中教材在编写过程中缺少对相应小学数学教材的关注,造成了“各自为战”,如在三角形内角和定理的教学时,不少教师“严守”某些教材的情境,安排不少教学时间让学生剪拼,为了得到一个180度的结论,却忘了问一下学生“你们知道三角形内角和吗?”这里可提及美国学者巴拉布与达菲对预设“好的问题”的建议:“教师的工作是通过向学生问他们应当自己问自己的问题来对学习和问题解决进行指导,这是参与性的,不是指示性的;其基础不是要寻找正确答案,而是针对专业的问题解决者当时会向自己提出的那些问题.”[6]这就是指,能够提出恰当的问题正是唤起数学活动经验的有效保证.
1.史宁中.数学思想概论(第1~5辑)[M].长春:东北师范大学出版社,2008、2009、2009、2010、2012.
2.[日]米山国藏.数学的精神、思想和方法[M].成都:四川教育出版社,1986.
3.郑毓信.教师专业成长的主要目标与重要内容(下)[J].小学教学(数学版),2013(12).
4.齐民友.数学与文化[M].长沙:湖南教育出版社,1991.
5.[日]佐滕学.21世纪学校改革的方向[J].人民教育,2014(1).
6.乔纳森,等,主编.学习环境的理论基础[M].上海:华东师范大学出版社,2002.FH
