重视—逻辑连贯，促进自主学习— 以“等腰三角形的轴对称性”教学为例

☉江苏省南京市莲花实验学校 吉明华

重视—逻辑连贯，促进自主学习— 以“等腰三角形的轴对称性”教学为例

☉江苏省南京市莲花实验学校 吉明华

章建跃教授在文1中指出：“在课堂教学中，要以数学知识的发生、发展过程和理解数学知识的心理过程为基本线索，为学生构建前后一致、逻辑连贯的学习过程，使他们在掌握数学知识的过程中学会思考.”受此启发，在最近开设的一节“等腰三角形的轴对称性”公开课中，从教学预设到课堂教学，笔者追求“前后一致、逻辑连贯”，促进学生自主思考，帮助学生学会学习.本文就围绕该课的教学预设和课堂生成给出教后反思，与同行研讨.

一、教学预设简案

说明：备课时参考了南通李庾南老师的课例［2］.

1.教学目标

（1）体会轴对称的性质在研究图形性质中的应用.

（2）在实验操作获得对等腰三角形的性质的感性认识的基础上，通过推理论证培养学生的理性精神，提高他们的推理论证能力.

（3）掌握等腰三角形的性质，丰富学生的学习感受，激发学习兴趣.

2.教学重、难点分析

教学重点：等腰三角形的性质.

教学难点：将实验操作获得的感性认识进行理性概括与推理论证.

3.教学过程

（1）回顾轴对称图形的性质，动手操作，探究等腰三角形的性质.

①回顾轴对称图形的性质.

②有两边相等的三角形叫做等腰三角形.（给每个学生提供一个等腰三角形纸片，供其折叠研究）

③全班交流研究成果.

等腰三角形是轴对称图形，对称轴是底边的垂直平分线，也就是顶角的平分线、底边上的高、底边上的中线所在的直线.

预设追问：引导学生在两腰上变换对称点继续探究等腰三角形的对称性质.

④在实验操作获得对等腰三角形的性质的感性认识的基础上，推理论证，概括等腰三角形的性质定理.

已知：如图1，△ABC中，AB=AC.

求证：∠B=∠C.

预设意图：由学生作思路分析，教师点评.给出如下板书.

性质定理1：等腰三角形的两个底角相等（简写成“等边对等角”）.

几何符号语言：略.

性质定理2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）.

几何符号语言：略.

（2）通过等腰三角形的性质定理的应用练习，体会知识的价值，激发进一步研究等腰三角形的兴趣.

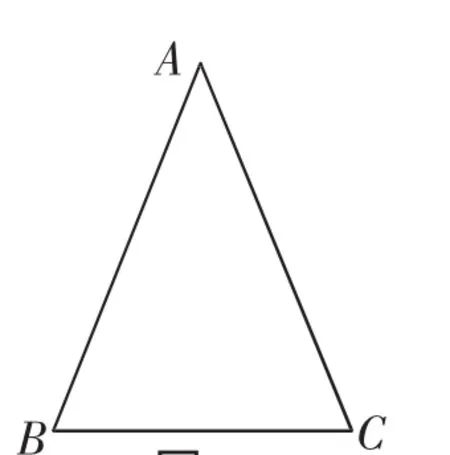
图1

练习1：如图2，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD.求△ABC各角的度数.

练习2：从一副三角板出发……

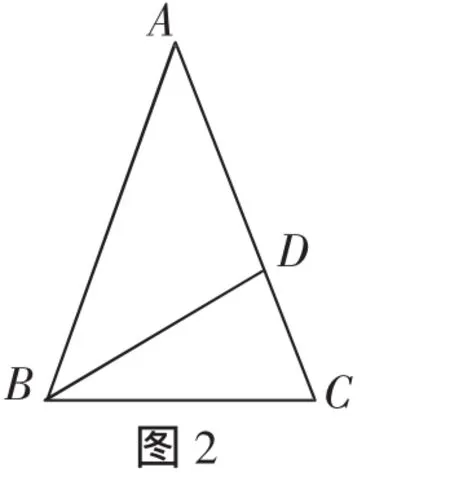
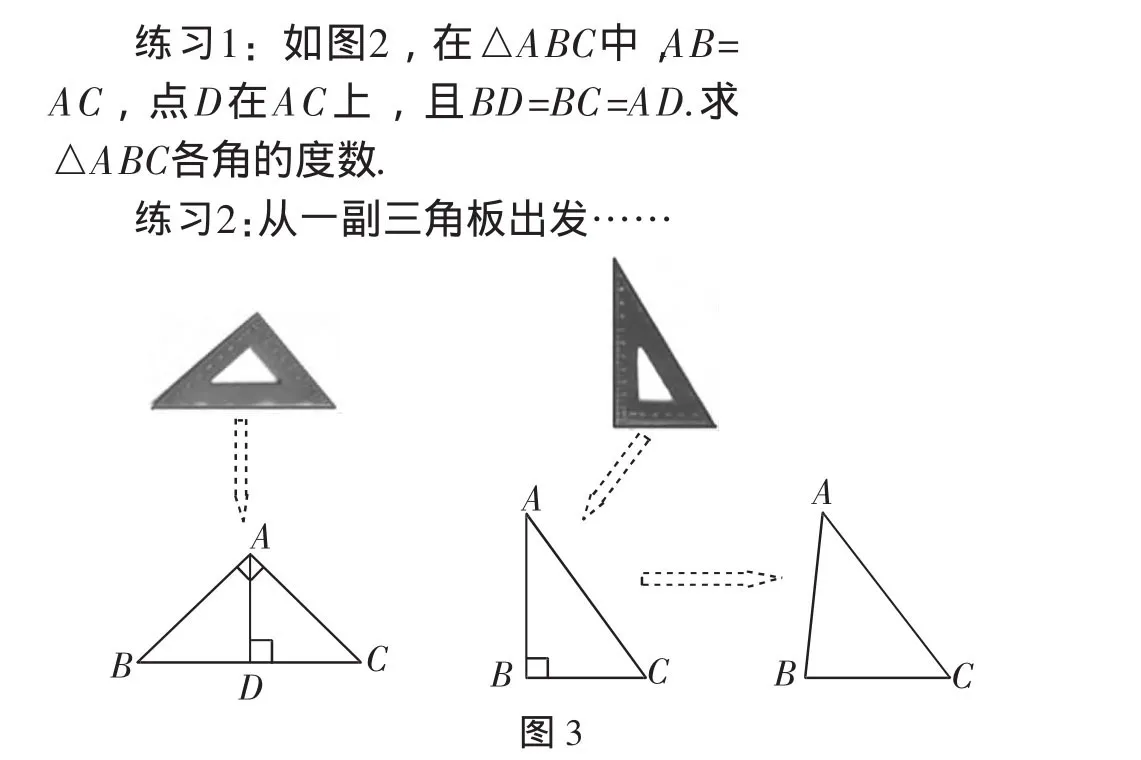
预设意图：在图3中，由一副三角板出发，追问学生哪一个是等腰三角形，并由等腰直角三角形添加底边上的高再分出新的等腰三角形，进一步巩固“等边对等角”；而由另一个特殊直角三角形认识到不等边所对的角也是不相等的，进而变式到一般三角形后发现“大边对大角”的性质，并探究其证明.

（3）课堂小结、布置作业.（略）

二、课堂生成片断

片断1：开课阶段，师生回顾轴对称与轴对称图形.

师：在轴对称的学习中，同学们对轴对称、轴对称图形有怎样的认识？

生1：轴对称图形被对称轴分成的两部分全等，这两部分关于对称轴对称.

生2：如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线.

生3：对应线段或其延长线如果相交，则交点在对称轴上.

……

图4

片断2：在学生个人折叠等腰三角形纸片的研究基础上，小组内交流，再全班汇报.

生4：我们小组交流后，有如下发现：如图4，直线AD是等腰△ABC的对称轴，由轴对称性质可得△ABD≌△ACD，故∠B=∠C，∠ADB=∠ADC=90°，∠BAD=∠CAD，BD=DC.

师：你的意思就是等腰三角形的两个底角相等（利用PPT演示翻折变换），还有等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

生5：我们小组还有一些发现：如图5，取腰AB、AC的中点E、F，连接BF、CE、DE、DF.

由轴对称性质可得AE=AF，BE=CF，DE=DF，△AED≌△AFD，△EBD≌△FCD.

图5

根据全等三角形中的对应边、对应角相等，BF、CE的交点Q在AD上，BF=CE，QE=QF，BQ=CQ，连接EF，图中有等腰△QBC、△QEF、△AEF等.

师：正确！你们基于轴对称的性质发现了很多有意义的结论！其他小组还有吗？

生6：等腰△ABC的对称轴上的任一点与两腰上的对称点的连线都分别相等.

师：很好！以上的发现都源自等腰三角形的本质特征——轴对称图形，对称轴是底边的垂直平分线，因而我们通过作出等腰三角形的对称轴，得到两个全等的三角形，从而利用三角形的全等证明等腰三角形的这些性质.

片断3：本课最后阶段，师生探究“大边对大角”.

师：同学们的直觉很好，猜想和发现了三角形中“大边对大角”，我们还需要针对这个性质说点理，可将问题抽象出来：如图6，在△ABC中，AB＞AC，求证：∠C＞∠B.

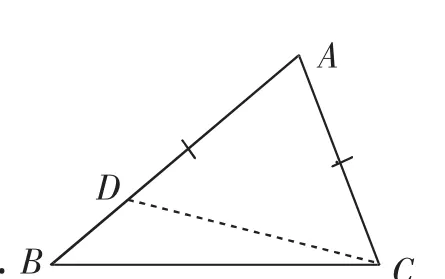
图6

生7：受“等边对等角”启发，在AB上截取AD=AC，构造一个等腰△ADC，则∠ADC=∠ACD（等边对等角），而∠ADC是△DBC的外角，所以∠ADC＞∠B，于是∠ACD＞∠B.又因为∠ACB＞∠ACD，则∠ACB＞∠B.

师：正确！“等边⇔等角”反映了同一三角形中边角之间相等的转化关系.在客观世界中，“相等”与“不相等”的关系是普遍存在的，有时“相等”与“不等”之间既对立又可以相互转化.生7的证明让大家感受到“等边⇔等角”经过构造转化后，也是证明“大边⇔大角”的理论依据.

三、教学反思

1.选好课堂起点，重视逻辑连贯

“求木之长者，必固其根本；欲流之远者，必浚其泉源”.关于课堂的起点，很多课堂都追求一段生动的“情景引入”，往往展示一些现实背景，并要求学生举出生活实例，然后从中抽象出研究的对象.近读《中学数学》，有选手在地级市的赛课时预设了如下的情境引入［3］.

电脑播放视频及独白：美丽的大森林，有人在破坏它，有人却在执着地呵护它.杨善洲，在第十届感动中国年度人物评选中，获得感动中国人物称号.他担任领导，两袖清风，为了兑现自己的承诺，扎根大山，义务植树造林，建成价值3亿元的林场，且将林场无偿捐给国家.同学们，假设老人的家乡，以前森林是一个长p千米，宽a千米的长方形（图略），经过杨善洲多年努力，森林的宽度增加了b千米，扩大后，森林的面积是多少呢？

正如该文作者点评的“以‘杨善洲造林’这个虚拟的情境替换教材中原来的情境，前者给人以造假、情境失真之感，而后者则自然、到处可见”.事实上，作为课堂教学起点，不仅要考虑这一堂课内的逻辑连贯，而且要考虑整个章节、单元、学期甚至学段知识链上的逻辑连贯.上文在“生成片断1”中，开课阶段引导学生回顾轴对称与轴对称图形的性质，正是引发学生关注整个知识链上的逻辑连贯.这里也可顺便提及世界知名几何学家伍鸿熙教授提出的数学的基本原则［4］，比如“数学是连贯的，数学的概念和方法组成了一个逻辑严密的整体”.可见，数学学习必须按照数学知识发展的这种逻辑系统而循序渐进，不能随意超越、跳越.数学学习的这个特点与其他学科的学习是很不一样的.

2.重视基本套路，促进自主学习

章建跃教授在文5中强调要重视“基本套路”的教学，如代数教学中，无论是数、式、方程、不等式，都应强调从运算的角度发现和提出问题、分析和解决问题，并称这就是“代数的整体性”.而具体对象的研究中，则要遵循“定义—表示—性质—公式、法则……”的“基本套路”.在上面的教学案例中，我们在探究等腰三角形的性质时，引导学生经过独立自学（操作探究）、小组交流，然后全班汇报，在课堂生成“片断2”中，学生基于轴对称的性质发现并证明了等腰三角形的性质定理；由于不少等腰三角形问题只是关注了一些特殊点，如腰上高的垂足，腰的中点，底角平分线与腰的交点，而生5、生6却将问题向更丰富的性质上拓展，发现了“等腰△ABC的对称轴上的任一点与两腰上的对称点的连线都分别相等.”让学生在“基本套路”的引导下，促进自主学习，学会学习，以教达到不教的目的，永远应该是我们的追求.再有，在课堂最后，我们还引出“大边对大角”这一看似多余的变式追问，这也是要向学生渗透“对立统一”、“矛盾转化”等辩证唯物主义观点的教育.

四、结束语

作为文末，笔者还想推介最近读到的一则关于数学的比喻［6］.

想象一个平原上面有一座巨大的直入云霄的隐形大厦.因为它对平原及周围气候产生的影响，我们知道它就在那里.人们在看起来是大厦的底部周围种上藤蔓的种子，藤蔓沿着隐形的墙生长，沿着角落、裂缝的雕塑摸索它自己的路，缓慢勾勒出那里的一些东西的轮廓.藤蔓没有随意生长，因为它需要持续的照顾.它需要水、肥料，甚至需要导向，所以需要园艺师.这些管理者在地上或者站在摇晃的高梯子上不断地修剪和拨开藤蔓.结果就是藤蔓的形状以及它似乎要形成的轮廓不仅反映出其中的大厦，也反映出园艺师的兴趣和日常工作.

想来，作为中学数学教育人，有责任、有义务向学生传授逻辑连贯的数学教学.惟有这样，数学作为一座“隐形大厦”，才能让更多的学生知道并确信“它就在那里”！

1.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

2.李庾南，陈育彬.中学数学新课程教学设计30例——学力是这样发展的［M］.北京：人民教育出版社，2007.

3.蔡宏.教学预设时对教材内容的“加减”之思——由一次市级赛课的教案说起［J］.中学数学（下），2014（1）.

4.章建跃.数学课要教数学［J］.中小学数学（高中版），2012（6）.

5.章建跃.课堂教学要注重数学的整体性［J］.中小学数学（高中版），2013（5）.

6.Greg McColm.数学教育的一个比喻［J］.姜红，译，陆柱家，校.数学译林，2012，31（3）.