双参换元，构造二次曲线巧解含根式问题

☉江苏省泰兴中学 吴卫东

双参换元，构造二次曲线巧解含根式问题

☉江苏省泰兴中学 吴卫东

一般来说，利用代数方法解决含根式的问题比较繁琐，因为对根式而言，变形的主要方法是平方.由上面的简单例子可以看出，函数与方程之间存在着必然的联系.本文结合近几年来的竞赛或高考试题，通过引入两个变量，即双换元的方法，将代数中的根式问题转化为解析几何中的二次曲线问题，总结出几种常用的转化途径.

途径1 转化为二次曲线上的动点与定点之间的距离问题

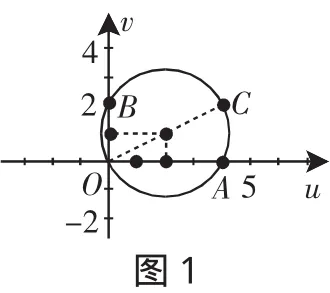
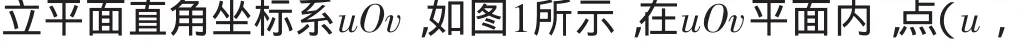
点评：引入双参数后，转化为圆上的动点到一个定点的距离的范围问题.

途径2 转化为二次曲线的动点到一定直线的距离问题

点评：（1）引入双参数，转化为圆上的点到定直线的距离的范围问题；

途径3 转化为过二次曲线的点的直线系的纵截距问题

例3（2013年全国高中数学联赛江西预赛）

途径5 转化为二次曲线上的点与定点连线的斜率问题

总之，通过引入双参数，将根式变为有理式，充分挖掘代数式所隐含的几何特征（如距离、截距、斜率等），构建平面直角坐标系与二次曲线，利用点、直线与二次曲线的的关系（相切、过曲线弧的端点等），巧妙地将代数问题转化为解析几何问题去求解.