“矛盾”何处有 条条通“罗马”——反证法证明过程中的归谬分析

☉浙江省慈溪中学 陈红冲

“矛盾”何处有 条条通“罗马”
——反证法证明过程中的归谬分析

☉浙江省慈溪中学 陈红冲

反证法是间接证明中一种非常重要的证明方法，无论在高考中还是在竞赛中都能找到其强大的用武之地.本文针对反证法证明的关键步骤——归谬分析，详细阐释了何处发生矛盾、如何找出矛盾以及用“活”反证法这三个方面，以此提高学生的数学思维能力.

一、问题的提出与思考

笔者在很多堂的听课过程中发现：教师一般只讲授反证法的概念、反证法的基本步骤以及反证法的适用题型，但是对如何准确运用好反证法中归谬这一步骤缺乏详细的指导.笔者翻阅了高中数学选修2-2教师教学用书中“直接证明与间接证明”这一节，教材推荐3个课时，除去直接证明的教学课时，反证法的教学至多2个课时，同时学科指导意见（理科）推荐1个课时.但在实际教学当中，笔者认为这些课时是不够的，主要原因有以下两点：

（1）反证法是广泛应用的数学证明方法，甚至在某些问题上，只能用反证法，其重要性可见一斑.特别是历年高考数学经常出现反证法的试题足以说明要重视反证法教学以及增加课时的必要性.

（2）虽然在平时的教学中时常出现反证法的试题，但是对反证法的证明缺少系统、详细的认识；虽然课堂教学中教师对反证法的概念、证明步骤以及适合反证法的题型讲解较多，但对证明中的“归谬”这一关键步骤何处发生矛盾、如何选择矛盾的焦点缺乏准确的认识，因此需要集中时间指导学生学习反证法.

二、反证法步骤的“再认识”

1.如何“引向矛盾”

对原结论否定的假定的提出，相当于增加了一个已知条件，使得在证明过程中发生矛盾的可能性增加了，从而增加了反证法证明方法的总数，具体如何“引向矛盾”，笔者在例1中引用孙维刚［1］老师的一个经典例题三种证明并补充第四种证明来说明.

例1 求证a，b，c为正实数的充要条件是a+b+c＞0，且ab+bc+ca＞0和abc＞0.

分析：为了便于分析，将a+b+c＞0，且ab+bc+ca＞0和abc＞0分别标记为条件（1），条件（2），条件（3）.

因为a，b，c为正实数，显然易得a+b+c＞0，且ab+bc+ ca＞0和abc＞0.即“必要性”的证明易于直接完成.

证明“充分性”时，要综合考虑三个不等式，推出a，b，c∈R*，有些难度，于是，尝试反证法.

证法1：证充分性：若a，b，c不全为正实数，由abc＞0，则它们只能是二负一正.不妨设a＜0且b＜0且c＞0，又由于ab+bc+ca＞0圯a（b+c）+bc＞0.

因为bc＜0，所以a（b+c）＞0，（*）

又a＜0，所以b+c＜0，（**）

而a+b+c＞0圯a+（b+c）＞0，所以a＞0.

这与a＜0的假设矛盾.所以假设不成立，故结论成立.

小结1：在证明过程中，先利用条件（3）作出的假设与条件（2）得出中间结论（**）.

再结合条件（1）得出新的结论与假设矛盾.

证法2：证充分性：从（*）开始，如下进行推理：

因为a+b+c＞0圯a+（b+c）＞0及a＜0，所以b+c＞0.

又由a＜0圯a（b+c）＜0，这与（*）式矛盾.

小结2：在证明过程中，先利用条件（3）作出的假设与条件（2）得出中间结论（*），再利用条件（1）与假设得出中间结论，这个结论与结论（*）产生自相矛盾.

证法3：证充分性：若a，b，c不全为正实数，由abc＞0，则它们只能是二负一正.

不妨设a＜0且b＜0且c＞0，因为ab+bc+ca=c（a+b）+ab＞0，

所以ab＞c（-b-a）＞0及a+b+c＞0圯c＞-a-b＞0，

所以ab＞c（-a-b）＞（a+b）2，即ab＞（a+b）2.

小结3：在证明过程中，先利用条件（3）做出的假设与条件（2）条件（1）得出新的结论，这个结论与事实公理矛盾.

总结：以上充分说明，可能发生的矛盾，主要有：新结论与题设相矛盾；新结论与假设相矛盾；新结论与客观事实相矛盾；推理过程中的自相矛盾.

2.进一步“例证”

笔者从《不等式的解题方法与技巧》［2］一书中选取了一道含有两个条件的反证法试题，运用前面指出的方法进一步例证.

例2 证明或否定命题：若x、y为实数且y≥0，y（y+1）≤（x+1）2，则y（y-1）≤x2.

分析：结合条件y（y+1）≤（x+1）2与结论y（y-1）≤x2的结构相似，猜测结论是成立，又此题从正面证明很难入手，故采取反证法.

证法1：假设y（y-1）>x2，因为y（y-1）>x2≥0，所以y<0或y>1.又因为y≥0，所以y>1.

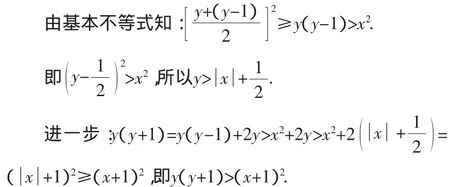
这与条件y（y+1）≤（x+1）2相矛盾.所以假设不成立，原命题成立.

证法2：假设y（y-1）>x2，因为y（y-1）>x2≥0，所以y<0或y>1.

若y>1，令函数t=y（y-1），易知t=y（y-1）在（1，+∞）单调递增，则

这与假设y（y-1）>x2矛盾，所以y>1不可能.

则只可能y<0，但这与条件y≥0矛盾.所以假设不成立，原命题成立.

证法3：假设y（y-1）>x2，因为y（y-1）>x2≥0，所以y<0或y>1.

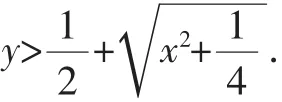
有条件y（y+1）≤（x+1）2和y>1可知

三、用“活”反证法

笔者曾在一高级中学中听了《间接证明——反证法》一堂课，对听课过程中的一道例题，引发了我对反证法的解题方法的进一步思考.

教师检查了两位学生在黑板上的解法，肯定了学生甲的做法，并对他的解题步骤作了有效的分析.当遇到学生乙的解法，该教师虽然口头上肯定了乙的想法，但由于事先的预设不够充分，又怕讲不完后续的例题，所以未将该例题讲透，这确实是教师备课过程中的一种遗憾.其实，我们只要用“活”反证法，还可以延续上面的内容……

证法1：要证明：x2+y2+x+y≥4xy，

即要证明：（x-y）2+2xy+x+y≥4xy，

只需要证明：2xy+x+y≥4xy，

即要证明：x+y≥2xy，

只需要证明x+y≤2.

从集合之间的关系看，题设中的条件x+y>2所表示的集合必须包含条件x+y≤2所表示的集合.显然这是一对矛盾，所以假设不可能成立，即原命题成立.

解这个一元二次不等式得：0 2相矛盾.

笔者以为反证法虽然是间接证明的一种基本方法，但是当对原结论否定的假定提出以后，命题的证明又回到了直接证明的状态，因此我们就可以选择适当的证明方法或把不同的证明方法结合使用，从而真正用“活”反证法.

1.孙维刚，著.孙维刚高中数学/孙维刚教育文丛［M］.北京：北京大学出版社，2005.

2.苏勇，熊斌，编著.不等式的解题方法与技巧［M］.上海：华东师范大学出版社，2011.