含表面裂纹X80管道的失效控制参量及计算
2014-01-30薛婷婷
田 涛,李 洋,薛婷婷
(1.中国石油集团石油管工程技术研究院,西安 710077;2.西安法士特汽车传动有限公司,西安 710119)
0 前 言
工业的发展对石油天然气需求急剧增加,为了提高输送效率,管线钢朝着大直径、高压力的方向发展。随着输送压力的增加,对管线钢强度的要求也越来越高[1]。尽管目前输气管道的主导用钢仍是以X70为代表的针状铁素体管线钢,但是高强韧性X80钢在西气东输二线工程中的大规模使用标志着我国高强度等级管线钢进入了一个新的发展阶段。
随着屈服强度的提高,屈强比呈升高趋势,这意味着应变容量的减小。然而,辛希贤等[2]的研究结果表明,硬化指数随屈强比的增大呈指数关系,而不是传统上所认为的线性关系。另外,一系列的准静态参量测试结果都表明高屈强比的X80钢管仍具有良好的韧性。实际上,管线钢在服役状态主要承受的是有内压引起的环向拉伸作用,与其他准静态力学参量相比,环向变形更能准确地表征材料的服役行为。
EPRG的试验结果表明,屈强比的提高会对环向变形产生不利的影响,如果管线钢存在缺陷,将会加剧这一影响[3],此时,断裂预测将成为一个重要问题,通常,一旦有裂纹存在,首先考虑到断裂韧性JIC,为此,JIC一般是由断裂韧性测试实验三点弯曲试验 (SENB)、紧凑拉伸试验(CT)单边缺口拉伸试验测得(SENT)得到,由于J积分的测量与裂纹尖端约束作用紧密相关,试样形状不同,裂纹深度不同,得到的断裂韧性结果则不同[4],朱先奎和 Brain N.Leis对 SENB和SENT试验结果分析表明[5],J-R曲线对裂纹深度有很强的依赖性,作者通过引入参数对裂纹尖端进行约束修正,并对含缺陷管道的临界内压做出了预测。 另外还有学者采用理论和数值方法对临界内压进行了预测[6-7],他们认为当韧带中的等效应力达到了最大抗拉应力(UTS)时,管道达到临界内压,还有人认为当等效应力达到90%的UTS时,管道达到临界内压[8]。而朱先奎等人采用平均剪应力屈服论理 (ASSY)并结合有限元(FEA)对临界内压进行了预测。预测结果相对其他失效屈服理论(Mises等效应力、Tresca屈服应力)更有效。而目前对含缺陷管道的环向变形的研究则比较少,本研究针对不同屈强比X80钢在含表面缺陷下的服役行为进行了有限元的模拟分析,计算管线钢的环向变形和裂纹尖端的J积分,并分析两个参量随内压的变化规律,并对两参量在含表面裂纹X80钢失效过程中所起的作用进行了探讨。
1 试验材料和试验方法
1.1 试验材料
本研究采用的三种不同屈强比的X80管线钢管,编号分别为1#、2#、3#,三种X80钢管的外径和壁厚相同,分别为1 219 mm和22 mm。
1.2 试验方法
屈强比为钢管屈服强度与抗拉强度的比值,通过单轴拉伸试验得到的试样应力-应变曲线获得。具体试验测定严格按照GB/T 228—2002《金属材料室温拉伸试验方法》标准在INSTRON 1341试验机上进行的。试验采用标准的圆棒拉伸试样,试样沿钢管环向截取,如图1所示,每种试验材料测试5个试样 (试验结果取其平均值),加载速率为1 mm/min。
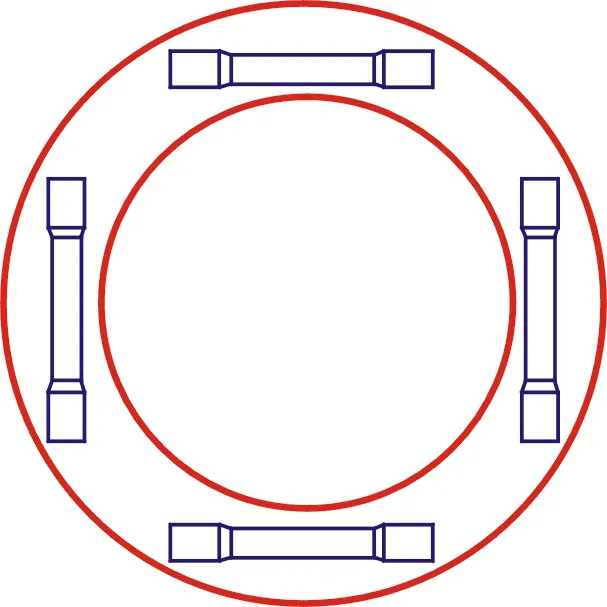
图1 拉伸试样截取示意图
通过三点弯曲试验测量X80钢管材料的断裂韧性,试样尺寸为 20 mm×10 mm×100 mm,取样位置与拉伸试样取样位置一致,整个试验过程参照ASTM1820进行。
有限元几何模型根据管道尺寸准1 219 mm×22 mm按比例1∶1建立1/2对称模型,材料的本构模型根据真应力应变曲线的应力应变点建立,单元网格采用plane183单元,裂纹尖端最小网格为0.002 mm,在这里裂纹尺寸分别取a/t=0.1,0.25和0.46(其中a代表裂纹深度,t代表管壁厚度),如图2所示。采用ANSYS12.0软件进行有限元计算,图3和图4代表性地给出了a/t=0.46时的有限元划分网格以及裂纹尖端的划分网格。
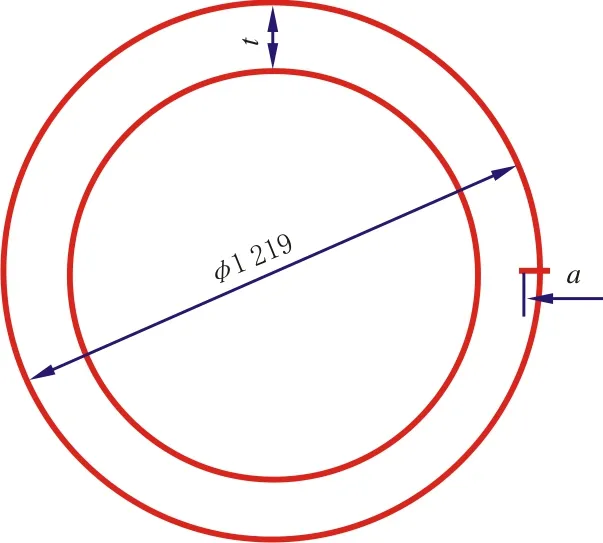
图2 含缺陷管道截面示意图

图3 模型网格划分示意图
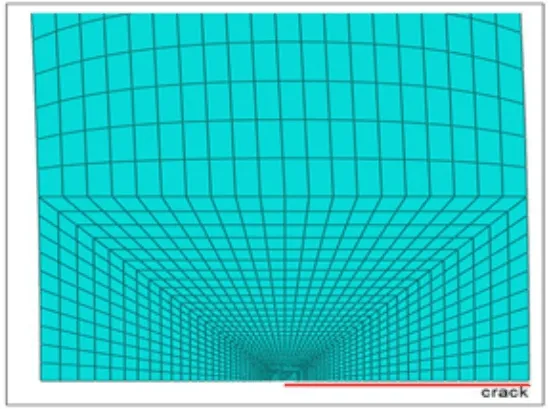
图4 裂纹尖端附近的网格划分示意图
环向变形是由管道内壁和外壁周长变化的平均值来表征。
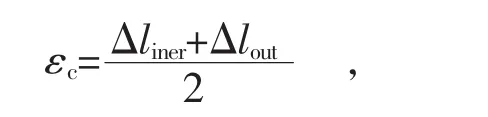
式中:εc—环向变形;
△liner—内壁周长变化量;
△lout—外壁周长变化量。
2 试验结果及分析
2.1 试验结果
三种X80钢的工程应力-应变和真应力应变曲线如图5所示,屈服强度与抗拉强度以及屈强比的测试结果见表1。结果表明,虽然都属于X80钢,该三种钢之间的屈服强度、抗拉强度以及屈强比存在着很大的差别。拉伸试验结果的另一个重要用途为有限元计算提供材料本构方程。
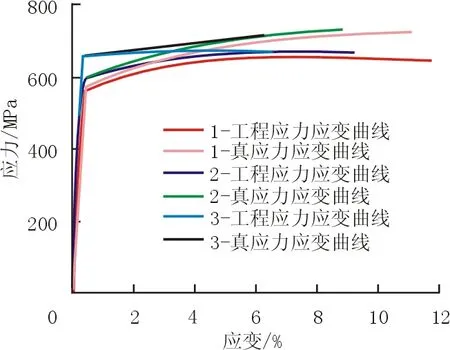
图5 三种X80钢不同屈强比的应力应变曲线

表1 三种X80钢力学性能测试结果
2.2 关于网格无关性的讨论
在有限元模拟分析时,网格的粗细程度对计算结果有很大的影响,通常网格越细,得到的结果越准确,反之误差越大,但网格太细,计算时间长,计算过程也难以收敛。这里对不同尺寸单元网格的裂纹尖端附近应力分布进行了比较,如图6所示,其中横坐标是韧带上距裂纹尖端的距离,纵坐标是对应的环向应力与屈服应力的比值。通过对比发现裂纹尖端附近单元尺寸从0.1 mm到0.001 mm,计算所得应力值越来越大,但是0.002 mm与0.001 mm的计算结果提高并不大,而且计算耗时。故以下计算都采用裂纹尖端附近单元尺寸0.002 mm进行计算。
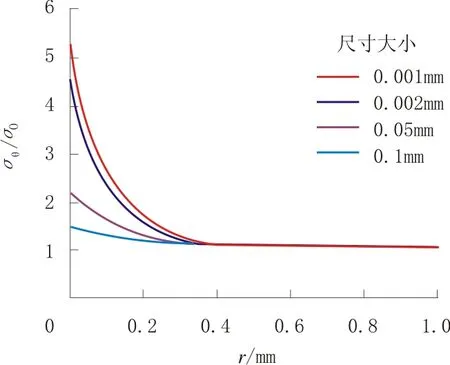
图6 不同单元网格裂纹尖端尺寸应力分布比较
2.3 计算结果分析
管道服役时主要承受的是由内压引起的环向拉伸作用,轴向裂纹的危害要高于环向裂纹,因此这里以轴向裂纹为例,采用有限元模拟计算裂纹尖端J积分随内压的变化。计算得到的J积分随内压的变化关系曲线如图7所示。在图7 中,图 7 (a),图 7 (b)和图 7 (c)分别为三种不同屈强比材料的J积分-内压p曲线。从图中可以看出,J积分随着内压的提高而增大,且每条曲线均存在一个临界点。当内压小于该临界点时,J积分的变化不明显;反之J积分迅速增大。可以认为该点代表着材料发生塑性变形的临界内压。
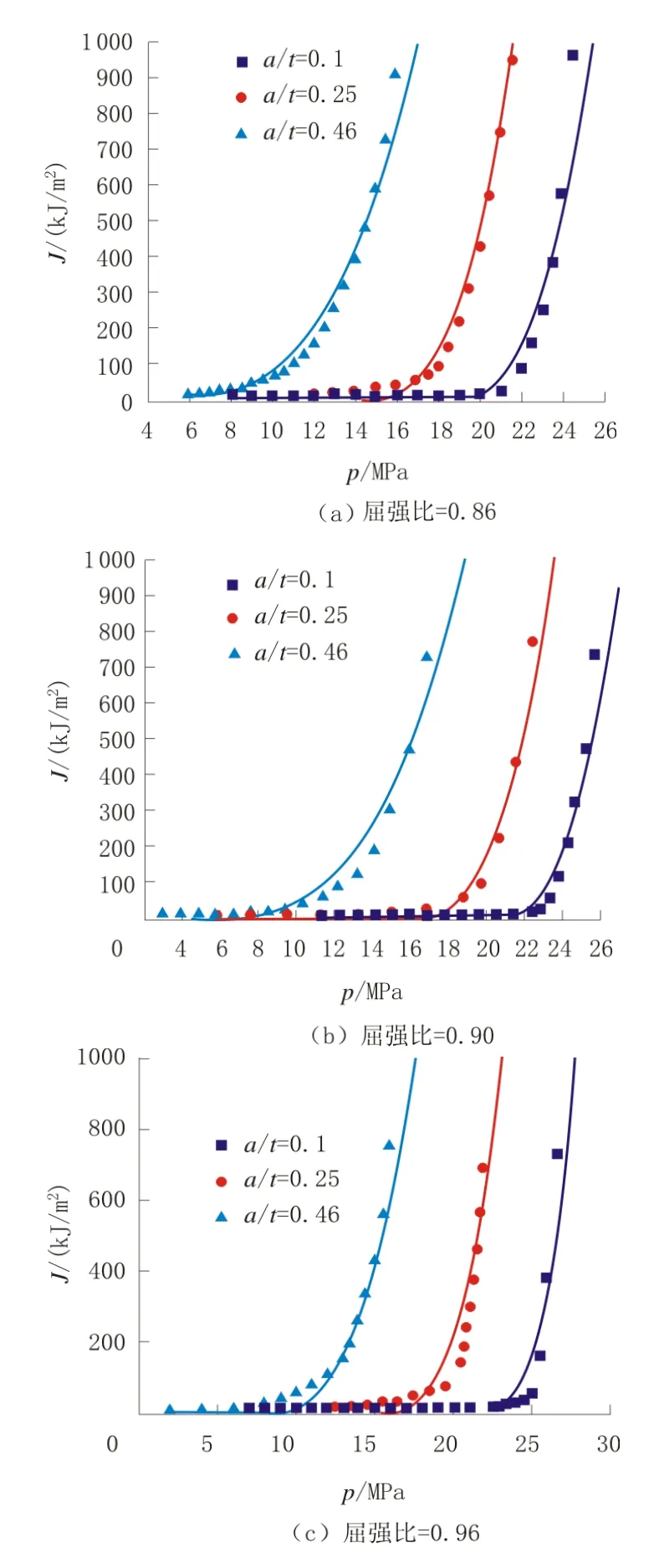
图7 3种不同屈强比材料的断裂纹韧度随内压的变化
类似地可以采用ANSYS计算得到管线钢环向变形随内压p的变化趋势,如图8所示。环向变形随内压的变化趋势与J积分的变化趋势大致相似,同样会随着内压的提高而增大。裂纹尺寸a/t=0.46时,环向变形随内压的增大趋势最明显。这是因为裂纹尺寸越大,管道壁厚韧带越窄,对变形约束作用越不明显。
为了分析J积分与环向变形对X80失效影响的相对大小,对计算结果进一步分析,得到了环向变形对应于J积分的变化曲线,如图9所示。本研究采用Zhu等人[10]的极限内压表达式
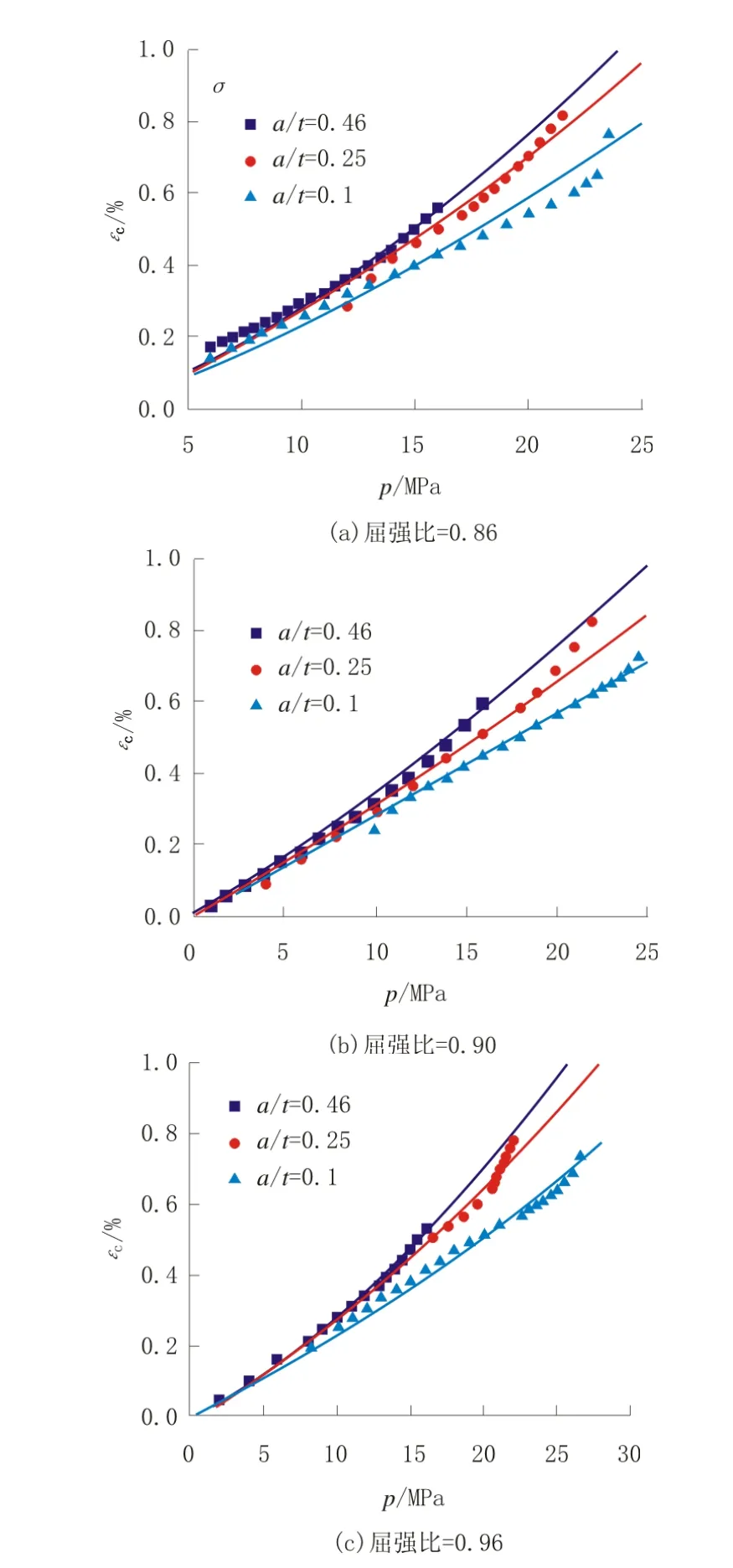
图8 3种不同屈强比的环向变形随内压的变化
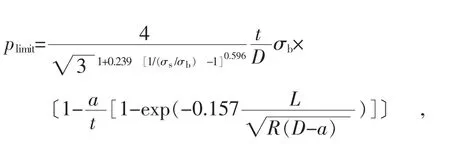
式中: plimit—极限内压; σs/σb—屈强比; a/t—裂纹深度; D—管道外径;R—管道半径,数值上等于D0/2。
得到了不同屈强比和/或不同裂纹尺寸下对应的极限内压plimit,定义与之相对应的环向变形称之为极限环向变形εlimit;在J积分与环向变形的曲线中,定义与极限环向εlimit对应的J积分为Jlimit。由图9可知,这些定义临界参量与材料本征断裂韧度JIC(试验测得)将εc-J曲线划分成三个区域:当J
3 结 论
通过有限元计算分析了X80钢在含表面缺陷下的失效行为及其控制参量。计算结果表明随着载荷内压的增大,J积分与环向变形都呈增大趋势,当内压大于某一临界值时,J积分突然增大;裂纹尺寸越大,环向变形的增大趋势越明显。通过极限环向变形εlimit和本征参量JIC可把断裂韧度J与环向变形的关系图分成了三个区域,分别是安全区域、J主导失效区域和环向变形εc主导失效区域。
[1]张华,赵新伟,罗金恒.X80管线钢断裂韧性及失效评估图研究[J].压力容器,2009,126(12):1-4.
[2]辛希贤,姚婷珍,张刊林,等.高屈强比管线钢的安全性分析[J].焊管,2006,29(04):37-40,90.
[3]SLOTERDIJK W,NEDERLANDSE GASUNIE N V.Effect of Tensile Properties on the Safety of Pipeline Steels [J].Brssels,1997,25 (11):34-35.
[4]DNV-RP-F108 (2006),Fracture Control for Pipeline Installation Methods:Introducing Cyclic Plastic Strain[S].
[5]ZHU Xiankui,BRIAN N L.Application of Constraint Corrected J-R Curves to Fracture Analysis of Pipelines[J].Int.J.Pressure Vessel Pipings,2006,128(12):581-589.
[6]FU B,KIRKWOOD M G.Determination of Failure Pressure of Corroded Linepipes Using the Nonlinear Finite Element Method [C]//Proceedings of the Second International Pipeline Technology Conference.Ostend,Belgium:[s.n.],1995:1-9.
[7]KARSTENSEN A,SMITH A,SMITH S.2001,“Corrosion Damage Assessment and Burst Test Validation of 8in X52 Linepipe [J].Pressure Vessel and Piping Design Analysis,2006,430(07):189-194.
[8]CHOI J B,GOO B K,KIM J C,et al.Development of Limit Load Solutions for Corroded Gas Pipelines[J].Int.J.Pressure Vessels Piping,2003,80(02):121-128.
[9]ZHU Xiankui,BRIAN N L.Theoretical and Numerical Predications of Burst Pressure of Pipelines[J].Journal of Pressure Vessel Technology,2007,129(11):644-652.
[10]ZHU Xiankui,BRIAN N L.Influence of Yield-to-tensile Strength Ratio on Failure Assessment of Corroded Pipelines [J].Journal of Pressure Vessel Technology,2005.127(12):437-438.
