计时攻击漏洞识别与防护能力量化评估技术＊

2014-01-24贺章擎童元满邹雪城

计算机工程与科学 2014年4期

关键词：样本数计时攻击者

贺章擎，戴葵，童元满，邹雪城

（1.湖北工业大学电气与电子工程学院，湖北武汉 430068；

2.华中科技大学光学与电子信息学院，湖北武汉 430074；

3.国防科学技术大学计算机学院，湖南长沙 410073)

计时攻击漏洞识别与防护能力量化评估技术＊

贺章擎1，2，戴葵2，童元满3，邹雪城2

（1.湖北工业大学电气与电子工程学院，湖北武汉 430068；

2.华中科技大学光学与电子信息学院，湖北武汉 430074；

3.国防科学技术大学计算机学院，湖南长沙 410073)

计时攻击是最具威胁的旁路攻击之一，为了设计安全高效的抗计时攻击的密码运算部件，需要在设计实现过程中及时发现密码算法的安全漏洞，并量化分析密码运算部件的抗计时攻击防护能力。因此，提出了一种可发现在密码算法具体实现中可能存在的计时攻击漏洞的分析方法。将密码算法采用增强数据相关图表示，通过在数据相关图中查找可被计时攻击的过程变量来分析安全漏洞，给出了相应的识别算法。并以成功实施计时攻击所需的样本数来量化密码运算部件抗计时攻击能力，提出了一种估算所需样本数的计算方法。

旁路攻击；计时攻击；增强数据相关图；量化评估

1 引言

近年来，以获取用户密钥为目的的旁路攻击越来越成为各类密码系统的严峻威胁［1］。计时攻击是一种重要的旁路攻击方式，通过获取系统工作时的时间信息来分析密钥，具有实施简单、攻击成功率高等特点，是目前最具威胁的攻击方式之一。计时攻击的概念由Kocher P C于1996年首次提出［2］。由于在密码算法的实现过程中常常存在一些冗余操作、条件或分支语句、高速缓冲存储器（Cache)命中状态以及处理器指令等，在用不同的密钥对不同的消息进行加密时，操作或指令等所消耗的时间会存在差异。密码分析者通过仪器测量出时间上的细微差别，通过分析就很可能发现密码机制中存在的弱点，进而破译出明文或密钥。

计时攻击的一个最新研究进展，就是Cache计时攻击［3］。现在软件实现的分组密码算法，例如高级加密标准AES（Advanced Encryption Standard)等，大都使用许多S盒查表法来提高效率，Cache计时攻击主要利用从Cache中加载数据到中央处理器CPU（Central Processing Unit)要比从随机存储器RAM（Random Access Memory)中要快的特性进行密码分析。通过测量密码算法实现过程中由于Cache访问带来的时间差异信息，攻击者可以推测密码算法实现的内部状态信息。同时，相比于其他旁路攻击方式，例如功耗攻击和电磁分析攻击，计时攻击还可以被应用到网络环境［4］，攻击范围更大，影响更深远。现在国内外针对计时攻击的主要研究方向，一是针对不同密码系统提出不同的攻击方法，二是针对已提出的攻击方法提出各种防护策略［5］。但是，在实际设计密码系统的过程中，常常需要在设计过程中对该系统抵抗计时攻击的能力进行评估，这样不但可以确保系统的安全性是设计者可以预测和可控制的，同时还可以在系统设计过程中及时发现问题并解决，可以缩短设计周期，降低设计成本，防止密码算法部件被过度防护，带来不必要的成本及性能开销。

在分析密码算法部件抗旁路攻击防护能力方面，国内外科研人员做了一定工作，不过大多数成果都是针对功耗攻击。例如，文献［6，7］提出了一种在设计的较早阶段计算密码运算部件抗功耗攻击防护能力的技术。文献［8］提出了一种密码部件抗电磁辐射分析攻击的防护能力量化分析技术。迄今还没有一个公开发表的针对计时攻击进行防护能力量化评估的成果。

2 识别密码算法中计时攻击漏洞的理论分析技术

为了对密码运算部件抗计时攻击的能力进行评估，首先需要分析其密码算法中是否存在可被计时攻击的可能。所以，本文的研究内容主要包括两个部分：一是分析密码算法具体实现中是否存在可被计时攻击的漏洞；二是当密码算法部件可能被实施计时攻击时，评估其实施的难度。下面首先给出识别密码算法中计时攻击漏洞的理论分析技术，包括算法表示，相应的公设和算法等；然后给出密码算法部件抗计时攻击防护能力的量化评估方法。

2.1 算法表示

为识别密码算法具体实现中可能存在的可被计时攻击的漏洞，首先要将密码算法采用一种合适的方式进行描述。文献［9］在数据相关图DDG（Data Dependence Graph)的基础上，提出了一种增强数据相关图EDDG（Enhanced DDG)。本文采用EDDG来对算法进行具体描述。关于EDDG的详细描述请见文献［9］，本文不再详述。

2.2 计时攻击漏洞的识别

将密码算法采用EDDG表示之后，下一步的关键是如何识别密码算法中是否存在计时攻击的漏洞。密码算法的执行时间存在差异主要是因为算法执行路径不同，而执行路径取决于条件转移变量。计时攻击的基本原理就是利用了一些条件转移变量与密钥相关，通过统计分析执行时间获取条件转移变量的信息从而推导密钥。例如，如果某个密码算法中存在以下分支：if（e＝＝1)then A；else B；在该例中e就是条件转移变量。如果执行A和B的时间存在可观测的差别，则攻击者即可根据时间样本的特性来确定e的值。假设e＝k1⊕p，如果p为攻击者已知量，则攻击者便可根据e和p的值推导出密钥k1。

公设1如果密码算法中存在满足如下条件的条件转移变量z，则攻击者可对z实施计时攻击以分析出密钥：

（1)条件转移变量z的表达式具有z＝f（k1，…，km，x1，…，xn)的形式，其中k1，…，km为可枚举的部分子密钥，x1，…，xn为攻击者已知量；

（2)令ki（1≤i≤m)为破解目标，如果令除ki之外的其他项为固定值，当ki取不同值时z的值不同，且执行路径的时间存在（可观测的)差别。

如果存在满足以上条件的条件转移变量z，则该密码算法中存在可被计时攻击的漏洞，攻击者可以针对z进行计时攻击从而分析出密钥ki。因此，分析密码算法具体实现中是否存在可被计时攻击的漏洞，就转化为在EDDG中查找是否存在满足公设1的条件转移变量z。

2.3 实例分析

文献［10］提出了一个基于随机加减法链的椭圆曲线加密算法ECC（Elliptic Curve Cryptogra-phy)实现技术，将其实现算法的主体循环采用EDDG表示，如图1所示，其中d为ECC算法的密钥，sub（d，j，l)表示d的第j位，e 为引入的随机数，state表示计算过程的状态，R和T 为中间结果，j为系数d当前位的索引。在图1中，v1为条件转移节点，节点v1对应的过程变量（state，e，sub（d，j，l))与部分密钥sub（d，j，l)存在数据相关且为可枚举的。与该过程变量相关的两条执行路径branch（0，1，1)和branch（0，1，0)分别为：｛R＝R＋T〈0，tpadd〉，T ＝2T〈tpadd，tpadd＋ttpdbl〉｝和｛T＝2T〈0，ttpdbl〉｝，其中tpadd、ttpdbl分别为点的加法和倍加操作的延时，显然这两条执行路径的运行时间存在明显的可观察的差别。

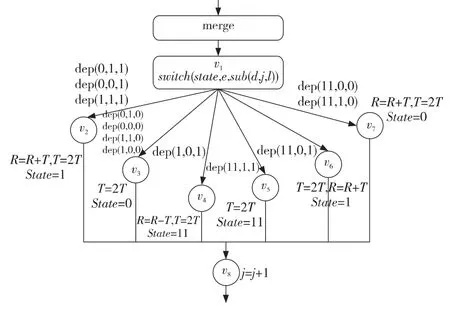
Figure 1 EDDG of ECC based on random addition subtraction chain图1 基于随机加减法链的ECC算法的增强数据相关图

对该算法EDDG进行进一步分析，列出算法某轮循环的状态表与执行时间如表1所示。

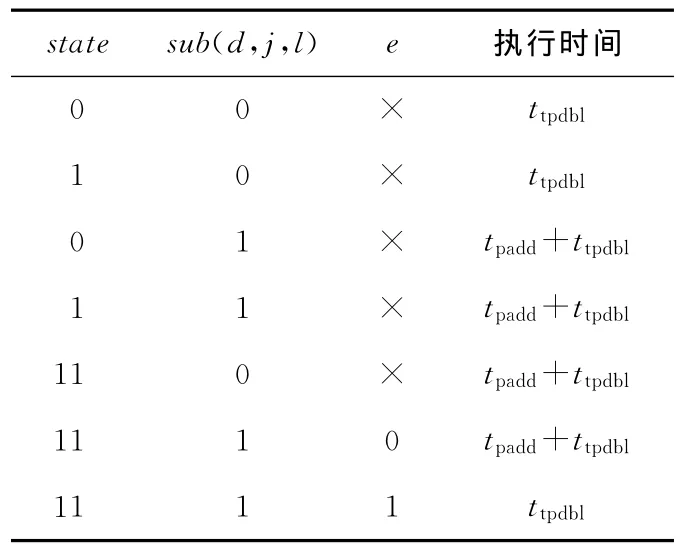
Table 1 State table and branching time in an ECC execution round表1 随机加减法链ECC算法中某轮循环状态表与分支执行时间

从表1可以发现，在某轮循环中，只有在state为11且sub（d，j，l)值为1时，执行时间被e随机化，其他情况下执行时间只与攻击者已知量state和密钥sub（d，j，l)相关，密钥sub（d，j，l)取值不同时执行路径不同且存在明显的时间差，所以该算法能被计时攻击。

3 密码算法部件抗计时攻击防护能力评估

识别出密码算法中计时攻击的漏洞之后，就需要评估攻击者成功实施攻击的难度。为了有效指导设计抗计时攻击的密码算法部件，需要在密码运算部件的设计实现阶段量化评估其抗计时攻击的防护能力。由于在实际的计时攻击中，很难直接获取某个分支或路径的时间信息，一般要通过大量的时间样本，采用合适的统计方法来进行分析。如果成功实施计时攻击中所需要的样本数越多，攻击难度就越大。当所需样本数超过一定数值时，攻击就变得不可行，所以本文以成功实施计时攻击所需的样本数来量化密码运算部件抗计时攻击的能力。文献［7］中提出了一种评估功耗攻击抵抗能力的量化算法，本文在其基础上进行了拓展，提出了根据计时攻击的信噪比来估算成功实施计时攻击所需样本数的计算方法。

3.1 计时攻击一般流程

根据前面的分析理论，如果发现密码运算部件的实现算法中某个条件转移变量z与可枚举的部分子密钥ki相关，且满足计时攻击的条件，则可对z实施计时攻击以分析密钥ki的值。攻击时，攻击者首先随机选取n个明文，使用目标密钥进行加密，获得n个时间样本。然后猜测密钥ki的值（假设为K)，并设定一个区分函数，根据区分函数将时间样本分为两个子集，如果统计发现这两个样本子集的均值存在明显的差值，则猜测正确，也就是目标的密钥即为K。

例如，在上例分析的ECC算法中，如果sub（d，j，l)取值为0，若此时state的值为0或者1，则对应分支的执行时间t1＝ttpdbl，若state值为11，对应的分值执行时间为t2＝tpadd＋ttpdbl，显然t1＞t2，时间差值是可区分的。如果sub（d，j，l)取值为1，则不存在这样的规律。所以针对该算法，攻击者可以首先猜测sub（d，j，l)的值为0，然后将state的值作为区分函数，将n个时间样本分为两个子集P1和P2，当state取0和1时对应的时间样本属于P1，否则属于P2。由于state的值可根据对应的明文获得，为攻击者已知量，所以这样的区分是可行的。然后攻击者统计分析P1和P2的均值，如果样本子集P1的均值小于样本子集P2的均值，则猜测正确，对应的密钥sub（d，j，l)的值为0。如果没有明显差值，则证明猜测是错误的，sub（d，j，l)的值就为1。这样就可获取sub（d，j，l)的值，采用同样的方法可以获得其他密钥的值直至全部密钥。

3.2 计时攻击信噪比的定义

为了进行量化评估，首先定义计时攻击的信噪比。对于执行时间未被随机化的密码部件来说，某次加密运算的时间是由明文p和密钥k决定的一个函数，也就是t＝f（p，k)，考虑到密码部件在执行和测量过程中会引入一些噪声等因素，所以假定对于不同的定长明文p和给定密钥k，执行加密运算的时间t为服从正态分布的随机变量［10］。

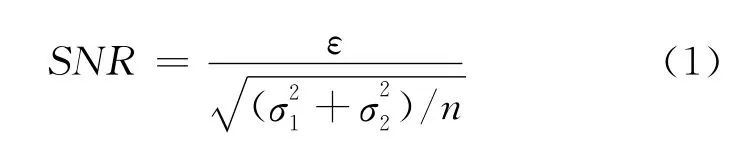
从上式可知，当样本数n增大时，计时攻击的信噪比将逐渐增大，攻击者实施计时攻击的难度逐渐降低，攻击成功的可能性将逐渐增大。

3.3 信噪比的计算

给出了计时攻击信噪比的定义之后，本文按照如下方法估算总体X和Y的概率分布，从而求出计时攻击的信噪比。

随机产生多个定长明文输入密码运算部件并采用未知密钥进行加密，获取n个时间样本。设加密的时间样本T服从参数为εi的正态分布，记为T～N（εi)。根据数理统计理论，εi和的最优无偏估计量分别为：

其中，n为样本容量，T1，T2，…，Tn为时间样本的值。在不同的设计层次下，以上时间样本可以通过时间分析模型、仿真软件或者测试仪器获取。

如果样本容量n足够大，则¯T和S＊2收敛于εi和。计算εi和的估计值的算法如图2所示。

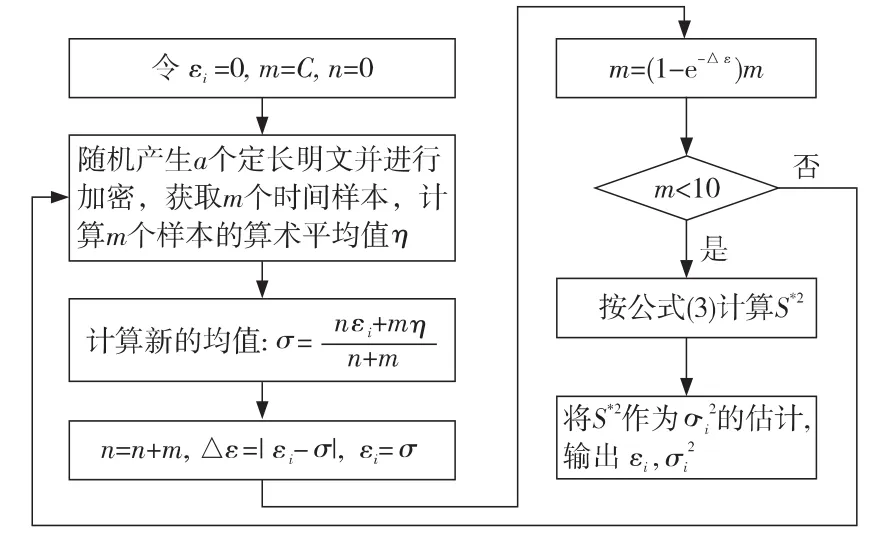
Figure 2 Estimates the mean and variance of the time samples图2 估算时间样本信息的均值和方差的算法流程图

该算法通过逐步求精进行计算，其中算法中的常数C为初始样本数，为一经验值，如2 000。根据上述算法可有效估计总体X和Y的均值和方差，从而求出时间偏差D的均值和方差ε和＋)/n。

3.4 成功实施计时攻击所需样本数的计算

得到总体X和Y的概率分布与无偏估计值后，便可求出时间偏差D的均值ε和方差＋)/n。由于D 服从参数为的正态分布，则D位于区间［ε－θε，ε＋θε］内的概率α为：

其中，Φ为正态分布函数。计时攻击的可信度取决于θ和α这两个参数的值，θ值越小，α的值越大，计时攻击的可信度就越高。为有效实施计时攻击，θ可取0.02，α取0.95，这样时间偏差D以大概率接近于ε。此时计时攻击所需的样本数n为：

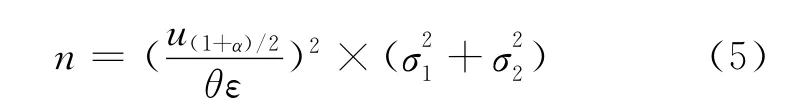
其中，u（1＋α)/2表示正态分布的（1＋α)/2的分位数。

需要指出的是，以上求得的是获取部分子密钥ki时所需的样本数。获取全部密钥所需的总的样本量，可以用获取所有密钥时所需的总样本数来表征。

4 结束语

本文给出了一种在密码算法设计阶段发现可能存在的可被计时攻击漏洞的分析方法；同时，以成功实施计时攻击所需的样本数来量化密码运算部件抗计时攻击能力，并且提出了根据计时攻击的信噪比来估算成功实施计时攻击所需样本数的计算方法。按照本文所述方法评估文献［2］中RSA算法实现的抗计时攻击防护能力，得到时间攻击的信噪比为0.66，成功实施时间攻击所需的样本数（置信度α＝0.95，θ＝0.02)为22 000左右。而文献［2］中实际攻击结果需要20 000个样本可恢复出密钥，说明本文所述的量化评估方法具有较高的准确度。结合密码算法部件防护能力的定性分析和定量分析技术，可以有效指导抗计时攻击的密码算法部件的设计与实现。

需要指出的是，本文提出的抗计时攻击量化评估技术，适用于通过统计分析大量样本的差分值来破解密钥的计时攻击方式。在进一步的研究工作中，将对本文提出的计时攻击漏洞的识别算法和量化评估技术进行进一步完善，扩展到其他类型的攻击方式上。另外，可以基于本文的研究成果建立密码系统抗旁路攻击的辅助设计EDA工具。

［1］ KULRD＆SCARD Consortium.Side channel attacks［EB/OL］.［2013-06-01］.http：//www.scard-project.org.

［2］ Kocher C.Timing attacks on implementations of diffie-Hellman，RSA，DSS，and other systems［C］∥Proc of the 16th Annual International Cryptology Conference on Advances in Cryptology，1996：104-113.

［3］ Bernstein D J.Cache timing attacks on AES［EB/OL］.［2013-06-01］.http：//cr.yp.to/papers.html〕cache timing.

［4］ Brumley B B，Tuveri N.Remote timing attacks are still practical［C］∥Proc of the 16th European Conference on Research in Computer Security，2011：355-371.

［5］ Oswald E.On side-channel attacks and the application of algorithmic countermeasures［D］.Graz：Graz University of Technology，2003.

［6］ Mangard S.Calculation and simulation of the susceptibility of cryptographic devices to power-analysis attacks［D］.Graz：Graz University of Technology，2003.

［7］ Tong Yuan-man，Wang Zhi-ying，Dai Kui，et al.Quantitative evaluation of the cryptographic blocks resistibility to power analysis at tack at different design level［J］.Journal of Computer Research and Development，2009，46（6)：940-947.（in Chinese)

［8］ Li Hui-yun，Markettos A T，Moore S.Security evaluation against electromagnetic analysis at design time［C］∥Proc of the 10th IEEE International on High-Level Design Validation and Test Workshop，2005：280-292.

［9］ Tong Yuan-man，Wang Zhi-ying，Dai Kui，et al.A unified method for identifying the feasible power analysis attacks in various implementations of cryptographic algorithms［J］.Journal of Computer-aided Design＆Computer Graphics，2008，20（3)：395-402.（in Chinese)

［10］ Oswald E，Aigner M.Randomized addition-subtraction chains as a countermeasure against power attacks［C］∥Proc of CHES’01，2001：39-50.

附中文参考文献：

［7］童元满，王志英，戴葵，等.不同设计层次下密码运算部件抗功耗攻击能力量化评估技术［J］.计算机研究与发展，2009，46（6)：940-947.

［9］童元满，王志英，戴葵，等.识别密码算法具体实现中潜在功耗攻击的理论分析方法［J］.计算机辅助设计与图形学学报，2008，20（3)：395-402.

Quantitative security evaluation against timing attacks in cryptographic algorithm

HE Zhang－qing1，2，DAI Kui2，TONG Yuan-man3，ZOU Xue-cheng2
（1.Department of Electrical ＆ Electronic Engineering，Hubei University of Technology，Wuhan 430068；2.School of Optical and Electronic Information，Huazhong University of Science ＆ Technology，Wuhan 430074；3.College of Computer，National University of Defense Technology，Changsha 410073，China)

Timing attack is one of the most threatening side-channel attacks.In order to design efficient cryptosystems against timing attack，it is necessary to find the vulnerability at design time and quantitative analyze the resistibility to timing attack of the cryptographic algorithms.The paper proposes a unified method for identifying the feasible timing attack in various implementations of cryptographic algorithms，which are described by the Enhanced Data Dependence Graph（EDDG)，and analyzes the timing attack vulnerabilities by finding some intermediary variable in the EDDG.The number of time samples required for a successful timing attack is used to characterize the resistibility，which is computed based on the signal-to-noise ratio of the corresponding timing attack.

side-channel attack；timing attack；enhanced data dependence graph；quantitative evaluation

TP309

10.3969/j.issn.1007-130X.2014.04.012

2013-06-05；

2013-10-28

国家自然科学基金资助项目（60973035，61202481)

通讯地址：430068湖北省武汉市湖北工业大学电气与电子工程学院

Address：Department of Electrical ＆ Electronic Engineering，Hubei University of Technology，Wuhan 430068，Hubei，P.R.China

1007-130X（2014)04-0639-05

贺章擎（1980-)，男，湖北天门人，博士生，讲师，研究方向为信息安全与数字集成电路设计。E-mail：ivan＿hee＠126.com

HE Zhang－qing，born in 1980，PhD candidate，lecturer，his research interests include information security，and digital integrated circuit design.

戴葵（1968-)，男，湖北恩施人，博士，教授，研究方向为高性能处理器系统设计与信息安全。E-mail：daikui＠mail.hust.edu.cn