椭圆曲线密码中抗功耗分析攻击的标量乘改进方案＊

张友桥，周武能，申 晔，刘玉军

（1.东华大学信息科学与技术学院，上海 201620；2.上海华虹集成电路有限责任公司，上海 201203)

椭圆曲线密码中抗功耗分析攻击的标量乘改进方案＊

张友桥1，周武能1，申 晔2，刘玉军2

（1.东华大学信息科学与技术学院，上海 201620；2.上海华虹集成电路有限责任公司，上海 201203)

椭圆曲线标量乘法运算是椭圆曲线密码（ECC)体制中最主要的计算过程，标量乘法的效率和安全性一直是研究的热点。针对椭圆曲线标量乘运算计算量大且易受功耗分析攻击的问题，提出了一种抗功耗分析攻击的快速滑动窗口算法，在雅可比和仿射混合坐标系下采用有符号滑动窗口算法实现椭圆曲线标量乘计算，并采用随机化密钥方法抵抗功耗分析攻击。与二进制展开法、密钥分解法相比的结果表明，新设计的有符号滑动窗口标量乘算法计算效率、抗攻击性能有明显提高。

椭圆曲线密码；标量乘；功耗分析攻击；滑动窗口算法；混合坐标系

1 引言

椭圆曲线密码ECC（Elliptic Curve Cryptography)体系由于其安全性高、密钥短、计算量小的优势逐渐成为首选的公钥加密方案，在智能卡、POS机等资源受限而安全性要求较高的领域里已经得到广泛应用。椭圆曲线标量乘算法是ECC中最主要且最耗时的运算过程。已有大量学者对椭圆曲线标量乘快速算法做了研究，常用的有二进制展开法、滑动窗口法、NAF（Non Adjacent Form)［1］算法等。文献［2，3］则研究了选择不同坐标组合下的最优标量乘算法。

ECC标量乘法的计算是基于密钥k的点加（ADD)和点倍（DBL)组成的。近年来一种新型的攻击理论——功耗分析攻击［4］的提出给智能卡等设备中的ECC算法带来了巨大的威胁。攻击者无需知道ECC硬件系统实际电路结构，仅仅通过统计和分析密钥运算执行时的功耗与密钥的相关性就能破解密钥。因此，研究快速安全的标量乘算法成为椭圆曲线密码应用中的一个重要问题。

本文的研究目标是提高椭圆曲线标量乘运算的效率且确保其抗功耗分析攻击性能。基于椭圆曲线的点加及倍点计算在不同坐标系下运算速度不同，提出了一种在混合坐标系下采用有符号滑动窗口算法计算标量乘法的快速算法，结合随机密钥掩码的方法能有效抵抗功耗分析攻击。与常用算法对比表明，在安全性提升的情况下，计算效率有明显提高。

2 椭圆曲线密码

1985年，Koblitz N等人将椭圆曲线应用到密码学中，在公钥密码体制研究中取得了重大突破，这就是椭圆曲线上的密码体制ECC。基于ECC设计了椭圆曲线数字签名算法ECDSA（Elliptic Curve Digital Signature Algorithm)、椭圆曲线密钥 协 商 机 制 ECDH（Elliptic Curve Diffie-Hellman)及椭圆曲线综合加密方案ECIES（Elliptic Curve Integrated Encryption Scheme)。ECC以其强大的“短密钥”优势正逐步走向公钥密码的主舞台。

2.1 椭圆曲线密码原理

一条椭圆曲线是在射影平面上满足维尔斯特拉斯（Weierstrass)方程：

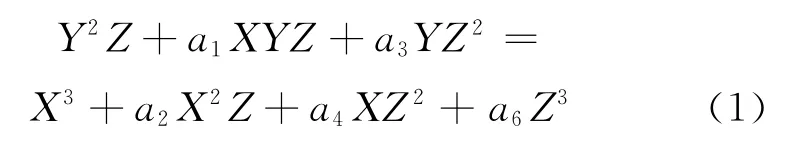
的所有点的集合，曲线上的每个点都是非奇异的，将X＝x＊Z、Y＝y＊Z代入齐次方程（1)得到：

也就是说，满足方程（2)的光滑曲线加上一个无穷远点O，组成了椭圆曲线。

椭圆曲线上所有的点和无穷远点构成的集合，连同一个定义的加法运算（点加)构成一个Abel群。此群中的任何元素P1、P2满足：P1＋P2＝P2＋P1。在等式kP＝P＋P＋…＋P＝Q中（P、Q为椭圆曲线上的两点，k为整数，“＋”为定义的点加，共有k个P相加)，已知k和点P求点Q比较容易，反之已知点Q和点P求k却是相当困难的。这个问题称为椭圆曲线上点群的离散对数问题 ECDLP（Elliptic Curve Discrete Logarithm Problem)［5］。ECDLP是比整数因子分解问题IFP（Integar Factorization Problem)和离散对数问题DLP（Discrete Logarithm Problem)难得多的数学难题。椭圆曲线密码体制正是利用这个难题设计而来的。

2.2 椭圆曲线标量乘法

标量乘法的计算是由一系列取决于密钥k的比特序列的点加和点倍运算来完成的，它们也被称为椭圆曲线操作。在椭圆曲线公钥密码体制中，加密、解密及签名、验证过程都需要用到标量乘法。标量有多种不同的表示方法，分别采用不同的运算方式。在智能卡等嵌入式设备中一般使用二进制表示标量。下面给出最常用的二进制展开法实现过程：

算法1二进制展开法

2.3 滑动窗口法

滑动窗口编码是指用一个宽度为w（一般w≥2，后续滑动窗口法均默认窗口宽度为w)的窗口对标量k重新编码。根据编码方式的不同可将滑动窗口算法分为无符号滑动窗口算法（记为USW2，k)和 有 符 号 滑 动 窗 口 算 法 （记 为SSW2，k)［6］。如果采用USW2，k对标量进行编码则k将被重新编码成由集合｛0，1，3，…，2w－1｝中的元素组成的数字串。如整数k＝1234567810＝BC614E16＝1011110001100001010011102，取w ＝3，则k重新编码（从左至右)后的结果为：

如果采用SSW2，k对标量进行编码，则对k的二进制序列以（w＋1)位为窗口长度进行分组，当窗口中的最高位为l时，表示窗口的值为负数，此时窗口的值用其对应的补码表示并产生一个进位。此时k的二进制序列编码（从右至左)是由集合｛－2w＋1，…，－3，－1，0，1，3，…，2w－1｝中的元素组成的数字串。编码过程中若最高位刚好有进位，即最后出现j的值大于l－1时，相应添加kj＝0。具体编码示例如：

算法2有符号滑动窗口法

3 功耗分析攻击及其防御方案

功耗攻击主要是利用密码芯片运算过程泄露的能量信息，结合密码算法的特点并运用统计分析方法来推测加密系统的关键信息。标量乘是ECC的最主要运算过程且易于遭受功耗分析攻击。功耗分析基本上分为两大类［7］：一类是简单功耗分析，包括一般的简单功耗分析SPA（Simple Power Analysis)以及倍点攻击DA（Doubling Attack)；一类是结合了统计学分析方法的差分功耗分析DPA（Differential Power Analysis)，DPA 又进一步延伸到高阶功耗分析 HO-DPA（High-Order DPA)、修正功耗分析RPA（Refined Power Analysis)以及零值点攻击ZPA（Zero-value Power Analysis)。

3.1 功耗分析攻击

简单功耗分析是根据测量加密系统的功率消耗轨迹，判断加密设备在某一时刻执行的运算过程以及此运算所对应的操作数，从而恢复出密钥信息。实施SPA需两个基本条件：（1)知道加密设备所使用密码算法的详细信息；（2)能精确采集到加密设备密钥运算的能量泄漏信息。一般有五种方法抵抗SPA：加入“虚”点加；使用已经归一化的标量乘法；使得标量乘法具有相同的运算模式而不依赖于标量；使用“统一”过的点加和倍点运算公式；使用所谓元子法［8］等。

差分功耗分析利用密钥参与计算来分析功耗差异和密钥的相关性，攻击者针对密钥运算获取大量功耗曲线来做统计分析。实施DPA的前提条件是加密设备密钥计算过程功率消耗与密钥值有相关性。抵抗DPA的方法主要是随机化，包括随机化密钥、基点和曲线等方法。

修正功耗分析是一种改进的DPA方法，攻击者选择一些特殊的有一个“0”坐标的点，使得椭圆曲线的随机映射和点的投影坐标随机化以及同态随机化无法对“0”坐标起作用。这样攻击者就能够使用DPA方法来分析密钥信息。抵抗RPA的主要方法是随机盲化基点和标量的随机分割。

零值点攻击是另一种形式的RPA方法，ZPA利用一类所谓“0”值点的特殊性质，用DPA方法分析得出密钥信息。与RPA类似，不能处理ECC坐标中“0”值的随机化方法面对ZPA时不安全，抵抗ZPA的主要方法是随机盲化基点和随机分割标量。

3.2 抗功耗攻击的二进制展开法

对算法1分析可知：运算是否执行椭圆曲线点加、倍点与密钥位的值密切相关，无法抵抗SPA。算法2对密钥进行了重新编码，有一定的抗SPA效果，但无法抵抗DPA。需对算法进行改进以在保证计算效率的同时提高算法的安全性。

对算法1的改进如算法3所示，采取基点掩码的方式增强算法的抗功耗分析攻击能力。

算法3抗功耗攻击的二进制展开法［9］

算法3首先选取了椭圆曲线上的一个随机点，每步计算过程随机点R都会参与运算。因每次运算过程产生的R会不同，因而不能靠统计功耗曲线分析密钥信息，可以抗DPA攻击。算法3的步骤3计算过程是倍点－点加的循环，与密钥位的值无关，故可以抗SPA攻击。因随机点参与计算因而不可能固定出0值，因此算法也抗RPA、ZPA攻击。

3.3 改进的滑动窗口法

目前已有许多研究者提出了对滑动窗口法进行改进的方案，文献［2］中提出了一种基于混合坐标系快速运算（2R＋S)［10］的方法来直接计算（2wR＋S)的快速标量乘法。在滑动窗口算法中，运用此算法可以大大减少椭圆曲线的标量乘的计算量。本文设计了一种基于密钥掩码直接计算（2wR＋S)的抗功耗攻击的滑动窗口算法。

算法4快速安全有符号滑动窗口法

选取一个随机数r，r与k具有相同的二进制位数且选取r＞k，置 m＝2k－r，n＝r－k。kP＝［（2k－r)＋（r－k)］P＝mP＋nP。

对m、n进行窗口为w的有符号滑动窗口法重新编码。编码方法及预计算同算法3中描述的执行步骤相同，在此不作详述。m、n有相同的长度，计算mP、nP的方法也完全相同。

分别计算出mP与nP后相加即可得到［k］P的值。

算法4采用随机化密钥的方法能有效抵抗DPA。DPA攻击之所以有效是因为每次使用的密钥都是相同的。如果加密时k是随机变化的，便无法形成有效的差分能量曲线，从而阻止了DPA攻击。首先选取了一个大于密钥的随机数，采用kP＝［（2k－r)＋（r－d)］P＝mP＋nP的方法来代替直接用k进行计算。每次生成的r随机，因此每次计算中标量的值与密钥无直接关系，无法得到算法输入与功耗的相关性，也就不可能通过DPA得出密钥。计算过程中将标量按有符号滑动窗口法重新编码后，采用直接计算（2wR＋S)的快速算法，计算为固定模式，也无法由功耗曲线得出密钥，故可以抗SPA。随机化密钥后每次r的不同会产生不同的编码，可有效抵抗RPA、ZPA攻击。总体上来说，采用随机掩码方式使计算过程标量与密钥无直接相关性，能有效抵抗各种功耗分析攻击方法。

4 算法效率分析与比较

在不同坐标系下椭圆曲线加法、倍点运算的计算量不同。文献［8］中给出不同坐标系下椭圆曲线点加和倍点的计算量，如表1所示。根据实际应用，密钥长度一般取S/M＝0.8，I/M 的值根据坐标系的选取及密钥长度的不同在9～30，本文取中间值，统一设I/M＝20（S、M、I分别代表有限域中的平方、乘法、模逆运算)。

算法4中计算过程为倍点和点加，根据表1计算可知，选用Chudnovsky Jacobian坐标系总的计算量最小。算法4共进行l次倍点运算及（l＋2)次点加计算，在Chudnovsky Jacobian坐标系下总的计算量为：l＊（6S＋5 M)＋（l＋2)＊（3S＋11 M)＝23.2lM＋26.8 M。

Table 1 Calculation of point addition and point doubling based on different coordinates表1 不同坐标系点加和倍点计算量

文献［8］中证明采用Affine加Jacobian混合坐标系直接计算（2wR＋S)最为快速，在此混合坐标系下直接计算（2wR＋S)的计算量为（4w＋3)S＋（4w＋9)M。

文献［11］证明用滑动窗口法进行标量乘运算时，长度为l bit的二进制标量在采用USW2，k进行编码后非零位的平均个数为l/（w＋1)。采用SSW2，k对一个l bits的二进制标量重新编码后，其非零位的平均个数为l/（w＋2)，因此采用SSW2，k编码方法后每次执行（2wR＋S)模式直接运算的窗口宽度平均为（w＋2)。算法4取随机数及其SSW2，k编码时间与椭圆曲线点乘相比可以忽略不计。

预计算中进行2w－1－1次点加计算及一次倍点计算（Affine坐标系下)，主循环进行2＊l/（w＋2)次（2w＋2R＋S)计算（Jacobian＋Affine混合坐标系)和一次点加计算（Jacobian坐标系)，算法4总的计算量为：

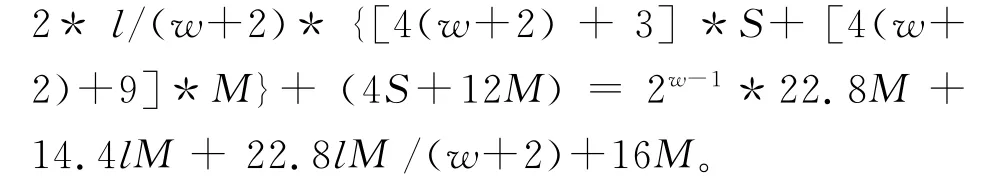
经分析计算，当椭圆曲线密钥长度l分别取160、192、224、256时，w 取3、4、4、4时计算量最小。

表2中对比了算法4及算法3、文献［12］中的密钥分解法的标量乘的计算量，其中，文献［12］在计算tpre时表述有误，应为：tpre＝（n－1)＊（m/n)＊DBLJ＋（n－1)＊tJ→A＋（2n－1)＊ADDA。

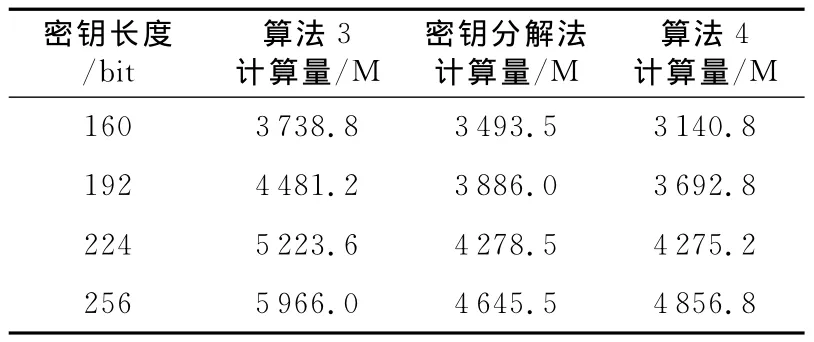
Table 2 Amount of calculation表2 计算量

由表2分析可知，密钥分解法在ECC密钥长度大于224位时有优势。一般说来，160位ECC密钥与1 024位RSA密钥安全等级相同，224位ECC密钥与2 048位RSA密钥安全等级相同。224位ECC密钥足够满足需求。且文献［12］在计算过程中采用加入随机点抗功耗分析攻击，未对密钥进行保护，其抗攻击性能远比不上本文使用的密钥掩码方法。由表2可得，密钥长度分别为160、192、224、256时算法效率分别平均提高13%、11.3%、9%、7%。总的说来，综合考量计算效率与算法安全时，本文设计的算法与其它标量乘算法相比有明显优势。

5 结束语

本文研究了抗功耗分析攻击的椭圆曲线标量乘快速算法，采用有符号滑动窗口算法提高计算效率，基于密钥掩码方法实现抗攻击性能。随机化密钥的方法使算法输入与密钥无直接相关性，能有效抵抗功耗分析攻击但增加了计算量，后续应重点研究更高效的抗功耗分析攻击方法，以提高椭圆曲线标量乘计算效率。

［1］ Solinas J A.Efficient arithmetic on Koblitz curves［J］.Designs，Codes and Cryptography，2000，19（2-3)：195-249.

［2］ Adachi D，Hirata T.Combination of mixed coordinates strategy and direct computations for efficient scalar multiplications［C］∥Proc of the Communications，Computers and Signal Processing，2005：117-120.

［3］ Cohen H，Miyaji A，Ono T.Efficient elliptic curve exponentiation using mixed coordinates［C］∥Proc of the Advances in Cryptology（ASIACRYPT’98)，1998：51-65.

［4］ Kocher P，Jaffe J，Jun B.Differential power analysis［C］∥Proc of the 19th Annual International Cryptology Conference on Advances in Cryptology，1999：1.

［5］ Zhang Fang－guo，Chen Xiao-feng，Wang Yu-min.The status of attack on the discrete logarithm of elliptic curves［J］.Journal of Xidian University，2002，29（3)：399-402.（in Chinese)

［6］ Liu Shuang－gen，Li Ping，Hu Yu-pu.Improvement schemes for scalar multiplication algorithm in elliptic curve cryptography［J］.Computer Engineering，2006，32 （17)：28-29.（in Chinese)

［7］ Zhang Ning.Elliptic curve scalar multiplication secure against power analysis attack［D］.Xi’an：Xidian University，2007.（in Chinese)

［8］ Chevallier-MAMES B，Ciet M，Joye M.Low-cost solutions for preventing simple side-channel analysis：side-channel atomicity［J］.IEEE Transactions on Computers，2006，53（6)：760-768.

［9］ Tong Lian，Qian Jiang.Scalar multiplication algorithm against SPA and DPA attacks in ECC［J］.Computer Engineering and Applications，2010，46（35)：72-74.（in Chinese)

［10］ Mathieu C，Marc J，Kristin L，et al.Trading inversions for multiplications in elliptic curve cryptography［J］.Designs，Codes and Cryptography，2006，39（2)：189-206.

［11］ Phillips B J，Burgess N.Implementing 1024-bits RSA exponentiation on a 32-bits processor core［C］∥Proc of the Application Specific-Systems， Architecture and Processor，2000：127-137.

［12］ Ma Bo，Bao Si-gang，Dai Xian-ying.Efficiency improvement of ECC resisting power attack scheme in smart card［J］.Computer Engineering，2010，36（16)：113-115.（in Chinese)

附中文参考文献：

［5］ 张方国，陈晓峰，王育民.椭圆曲线离散对数的攻击现状［J］.西安电子科技大学学报，2002，29（3)：399-402.

［6］ 刘双根，李萍，胡予濮.椭圆曲线密码中标量乘算法的改进方案［J］.计算机工程，2006，32（17)：28-29.

［7］ 张宁.能量分析攻击下安全的椭圆曲线标量乘法 ［D］.西安：西安电子科技大学，2007.

［9］ 童莲，钱江.椭圆曲线中抗SPA和DPA攻击标量乘算法研究［J］.计算机工程与应用，2010，46（35)：72-74.

［12］ 马博，包斯刚，戴显英.智能卡中ECC抗功耗攻击方案的效率改进［J］.计算机工程，2010，36（16)：113-115.

Improved scheme for scalar multiplication against power analysis attacks in elliptic curve cryptography

ZHANG You-qiao1，ZHOU Wu-neng1，SHEN Ye2，LIU Yu-jun2
（1.College of Information Science and Technology，Donghua University，Shanghai 201620；2.Shanghai Huahong Integrated Circuit Co.，Ltd.，Shanghai 201203，China)

Elliptic curve scalar multiplication is the main computing process in Elliptic Curve Cryptography（ECC)，and the efficiency and security of scalar multiplication is always the research hotspot.Aiming at the problem that elliptic curve scalar multiplication has a tremendous computation and is vulnerable to power analysis attacks，a fast sliding window algorithm against power analysis attacks is proposed.In Jacobian and Affine mixed coordinates，the signed sliding window algorithm strategy is used to perform elliptic curve scalar multiplication，and random keys method is applied against power analysis attacks.The analysis results show that，compared with binary expansion method and key assignment method，the improved signed sliding window scalar multiplication algorithm improves calculation efficiency and anti-attack performance significantly.

elliptic curve cryptography；scalar multiplication；power analysis attack；sliding window algorithm；mixed coordinates

TP309

A

10.3969/j.issn.1007-130X.2014.04.013

2012-09-17；

2012-12-30

国家自然科学基金资助项目（61075060)；上海市教育委员会科研创新项目（12zz064)

通讯地址：201620上海市松江区人民北路2999号2号学院楼424

Address：Room 424，2Academy Building，2999Renmin Rd North，Songjiang District，Shanghai 201620，P.R.China

1007-130X（2014)04-0644-05

张友桥（1988-)，男，湖北大悟人，硕士生，研究方向为密码算法和智能卡安全。E-mail：36xyz88＠163.com

ZHANG You-qiao，born in 1988，MS candidate，his research interests include cryptographic algorithm，and smart card security.