基于控制方法的风机塔架减振研究
2014-01-22陶学军卢晓光
陶学军,卢晓光
(许昌许继风电科技有限公司,河南许昌461000)
0 引言
大型风力机塔架占风力发电机整机成本的很大比重,塔架制造的主要成本是材料成本。现在风机塔架设计已由刚性塔架设计向柔性塔架设计转变[1]。怎样更好地控制塔架以减小塔架的振动,是进一步减小塔架材料制造用量、增加风机寿命的关键。另外,塔架是支撑机舱的结构件,塔架的振动传导到机舱上,导致机舱和叶片的振动增加,所以塔架振动的控制对减缓风机整机振动具有决定性意义。控制器可以通过变桨及转矩给定的微小改变算法对塔架进行加阻尼运算,有效抑制塔架振动。目前,已有大量学者对塔架加阻算法进行了研究[2-3]。相关文献都能给出了算法的过程和仿真效果[4],但是单纯的加阻算法在风机上应用所存在的风险都没能涉及。
本研究围绕塔架减载问题,研究塔架加阻的柔性振动控制技术,并分析实际应用减振算法的风险和避免方法。首先,分析引发大型变速变距风电机组塔架振动的原因和振动激励源特性;然后,以某2 MW 机组为例,进行振动特性分析,进行加阻滤波桨距控制器设计;最后,利用许继WRTS-800 和PRDS-600 仿真实验平台对控制策略进行综合验证分析,以疲劳载荷计算结果说明算法的有效性。
1 塔架振动原因分析
湍流及阵风扰动、尾流、风切变、偏航回转、塔影效应等引入的载荷波动,都是叶片振动的激励源,当塔架激励源振动频率和塔架的模态频率重合或接近时,就会导致塔架振动急剧增加,所以塔架的减振要从塔架的结构设计到控制器控制干预等设计运行过程全面考虑。首先,设计塔架时,塔架的一阶模态频率应在风轮1P 频率和3P 频率之间,因为风轮转速的1P 频率和3P 频率是塔架的主要激励频率,塔架一阶模态频率如果在1P 频率之下,则为提高塔架刚度必定增加塔架壁厚或增加塔架直径,导致耗材增加;塔架一阶模态频率如果在3P 频率之上,则因塔架刚度不足容易在运行过程中产生致屈曲的危险[5]。其次,为避免固有频率之间的耦合干扰风轮、机械传动链的固有频率不能于塔架的固有频率过于接近。再次,风机主要激励源频率是可以预知的,如由传动比与电机转速决定的1P、3P及6P 频率[6],塔架模态频率设计时应尽量避免接近这些已知敏感频率[7]。
由上述分析可知,正确确定塔架激励源频率是设计及控制塔架振动的先决条件。风轮转速引起塔架的激励源主要有2 个频率:①因质量不平衡导致的风轮旋转频率,即1P 频率;②因塔影、叶片平面内局部阵风等引起的以叶片穿越频率为基频的激励频率如3P、6P 等。
除上述确定性激励频率外,风机运行过程中,有很多不确定频率的激励,对塔架振动的影响也很大,最主要的有:风剪效应,即随高度增加风速成指数分布,其造成的风轮推力变化频谱包含所有频率成分;风的湍流变化,湍流风本身就是包含所有频率成分的激励源,所以造成的风轮推力变化频谱包含所有频率成分,风轮推力对塔架的作用力也就包含所有频率成分。
因此,与塔架模态频率接近的激励源是不能在设计过程中完全消除的,研究人员必须借助运行过程中的控制干预,以期尽可能地减少塔架振动。
2 塔架振动控制
2.1 机组坎贝尔图分析
风机主要激励对塔架振动的影响程度,以及风机各模态之间的耦合振动,研究者可以利用整机线性化模型及坎贝尔图加以分析。风机坎贝尔图可以反映整机各部件相互耦合之后的模态特性。在坎贝尔图中,包含了各部件耦合模态频率及各模态振动时相互影响的情况。当模态频率在风轮变速运行范围内,与1P、3P、6P 等包络线相交时,即为风机危险运行点,此时需重点分析该部件在相应运行转速下的振动阻尼情况及相应的特殊控制手段[8]。
仿真及分析工具在许继WRTS-800 风力发电机组仿真实验平台和PRDS-600 变桨距仿真实验系统中完成仿真计算工作。WRTS-800 和PRDS-600 仿真实验平台是为开发风机电控系统而设计的集成化仿真实验系统,具有完善的信号采集和信号模拟系统及灵活的通信方案,可方便连接各型号的主控及变桨实物;内部包含两套风机模型参数输入及计算方法,即以C 及Matlab 语言为平台的风机模型和以bladed 软件为平台的风机模型;平台可以通过提取风机各部件特征参数快速建立数学模型,可以对风力发电机组进行性能和载荷计算及控制器性能评估,是控制器开发、测试的有效工具;其中bladed 软件所采用的模型和理论方法[9],已得到多家公司的机组设计数据和实测数据的比对验证,被业界所认可。
仿真计算参数基于某2 MW 变速变桨机组数据,塔架高78 m,将其塔架划分为48 段。本研究在WRTS-800 和PRDS-600 仿真实验平台上建模并进行模态分析,塔架模态数据如表1所示。
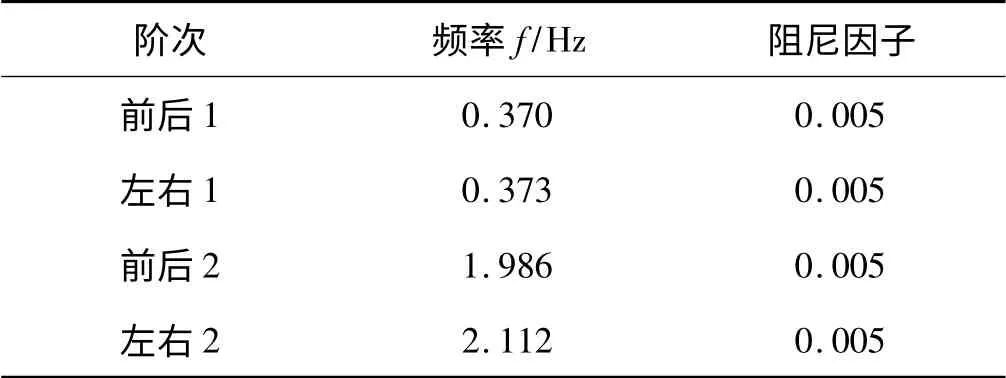
表1 塔架模态(风轮角方位0°)
机组谐振坎贝尔图(只重点显示塔架部分)如图l所示。可以看出机组的塔架1 阶前、后模态(频率0.37 Hz)和塔架1 阶侧向模态(频率0.373 Hz,与一阶前、后振动模态几乎重合,图中区分不开),在风轮转速11 r/min 时,和2P 斜线有交点,出现谐振情况。2P频率在风机运行中激励源能量不大,不属于主要激励源,在设计塔架时很难避免重合,一旦风机运行中控制0.37 Hz附近出现激励的较大能量集中,只能通过控制手段消除。
塔架2 阶前、后模态在13.4 r/min 时和风轮转速15P 频率有交点,出现谐振情况。15P 的激励源能量已经非常有限,这在对风机运行激励谱分析中可以清楚地看出,不到总能量的1%。
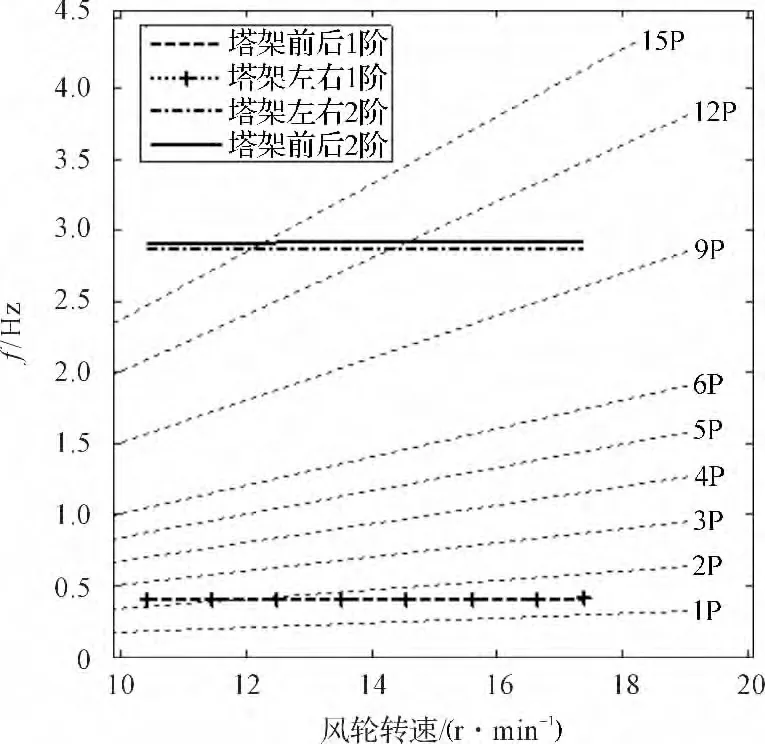
图1 塔架坎贝尔图
因塔架主要激励源能量与塔架1 阶模态比较接近,且在塔架前、后振动方向上,塔架振动主要考虑塔架一阶前后振动模态的影响。塔架坎贝尔图中塔架1阶前、后振动模态详细频率阻尼信息如表2所示。由表2 可知,风轮旋转和电机旋转都是塔架振动的主要激励源,风轮旋转中会包含风剪、湍流等引入的各种频率成分,那么对塔架1 阶前、后模态进行加阻控制就十分必要。

表2 塔架前后1 阶振动模态信息
2.2 塔架振动响应分析
塔架对振动源的响应可分解为自由振动响应部分和受迫振动响应部分。其中,自由振动响应频率由塔架模态频率决定,受迫振动响应频率由激励源频率决定。因阻尼的存在,风力机的自由振动的响应部分最终会衰减为0,对结构影响不大;故可只考虑塔架对受迫振动的响应部分。
假设激励频率为ω1,激励的输入载荷幅值为P,塔架模态频率为ω,则在不考虑阻尼项时,塔架振动的响应幅值可表示为:
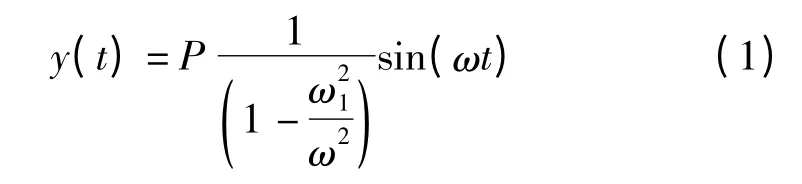
由式(1)可知,当ω1=ω 时,产生共振现象,即当激振力的频率与塔架模态频率重合时,振动位移将无限增加。当然,因塔架振动阻尼的存在,振动幅值不会达到无限大,但激励频率与塔架共振频率接近时,振动量会成倍增大。为避免运行中的塔架过大振动量,可以从前期设计和运行中控制两方面入手解决。
设计方面,尽量满足塔架的固有频率以避开风轮旋转频率、风轮3P 频率这两个主要激励频率的10%以上。塔架模态频率与主要激励频率相对差(高于额定风速段)如表3所示。其中,1P 频率为0.29 Hz,3P频率为0.87 Hz。由表3 可知,塔架在设计过程中避免了与主要激励产生共振。
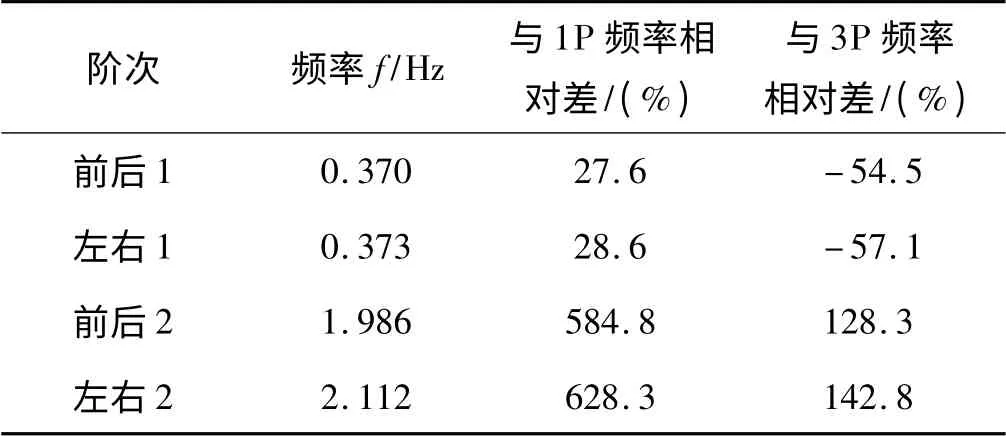
表3 塔架模态频率与主要激励频率相对差
2.3 塔架振动响应模型
塔架的动态响应模型可表示为2 阶阻尼谐振运动,如下式所示:

式中:x—塔架位移,m;F—塔架施加力,N·m,这里主要是风轮推力;ΔF—外部激励变化引起的附加推力,N·m;M,K—塔架模态质量与模态刚度。
在风机运行过程中,其塔架振动的1 阶前、后模态起主要作用。在塔架模态频率和外部激励源频率确定之后,塔架振动量和激励源振幅和塔架阻尼有关,塔架结构阻尼很小,其主要阻尼由气动阻尼提供,如果风轮的气动阻尼较小,小激励便可能引起很大的动态响应。在变桨距控制中,如果能提供一个塔架作用力ΔF,使ΔF 正比于-,则可以增大气动阻尼,达到塔架减振效果。对控制器来说,能通过改变桨距角来改变风轮推力,从而改变塔架上的推力。这一控制传递函数的输入是塔架的振动速度,输出是变桨角度变化量。因测量塔架的加速度较容易,实际应用时通过塔架振动加速度间接得到塔架速度。
通过风机模型的线性化矩阵,可以得到确定桨矩角下桨距角Δβ 的变化量导致塔架推力ΔF 的变化量,即∂F/∂β。那么由式(2)可知,总阻尼已变为:

2.4 塔架振动控制反馈传递函数设计
由仿真实验平台,可得到塔架加速度到桨距角输出的线性化模型(11 m/s 风速下):
依据式(3)可以设计需增加的阻尼传递函数增益范围。
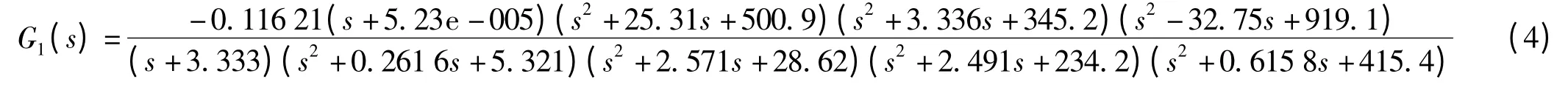
因塔架振动特定频率激励如3P 频率,虽然能量很大,但距离塔架模态频率很远,不足以引起谐振,在控制中不关心这样的振动响应,故此用一个陷波器与该反馈量串联起来,来滤除塔架加速度不希望出现在传函中的频率。滤波器的2 阶传递函数可表示为:(s2+)。
其中:如果ω1=ω2且ξ1=0,即为陷波滤波器,考虑到实验风机的额定风轮转速的3P 为0.87 Hz,取ω1=0.87 Hz;ξ2=0.4。
因变桨响应速度有限,对高频的输入信号,变桨系统根本响应不了,只能造成变桨无效动作,因此传递函数中需加入一个低通滤波器,其传递函数为1/(τs +1)。
其中:时间常数τ 的取值参考变桨模型响应速度参数,考虑变桨特性取τ=0.3。
设计塔架加阻传递函数如图2所示。
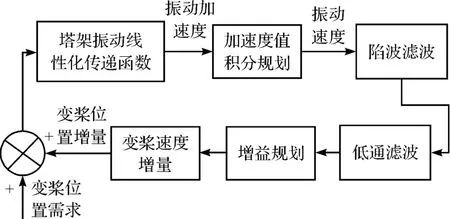
图2 塔架加阻反馈框图
其中,增益规划要根据式(3)的阻尼需求和控制器稳定性需求分析传递函数bode 图,在各个风速点上进行规划选取,是该传函设计工作量最大的设计点。在10.5 m/s 风速点,经规划,选择增益值为37.18。
2.5 加阻策略的暂时失效及应对
由于加阻算法要求施加力与塔架运动方向相反,本研究对调浆角度增量输出的相位要求比较严格。一旦相位相反,则加阻力即变为激励源。这种情况虽然在传递函数设计时进行了相位补偿,但在整个运行周期内还是不能完全避免。为防止这种现象,控制程序中利用塔架加速度信号经变换出加速度峰峰值这一监测信号,一旦峰峰值超过给定限值,则认为塔架出现谐振情况,控制器加阻使能关闭,并半功率运行固定的时间,以便使塔架脱离谐振状态。
3 控制性能分析
本研究在许继WRTS-800 风力发电机组仿真实验平台进行上述控制设计的验证,运行环境采用IEC61400-1-2005 规定的2 类风场湍流模型。笔者利用仿真平台对算法加入前、后进行疲劳载荷计算对比分析。
3.1 时域仿真数据分析
本研究在12 m/s 的湍流风下进行时域仿真,仿真数据表明,风轮转速及发电功率并没有因加阻减振策略的加入而有较大差别,说明策略的加入没有对整体控制造成影响。由策略加入前、后塔架前、后振动情况的部分时域数据可生成的机舱前、后x 方向加速度如图3所示,由图3 可知,减振效果明显。
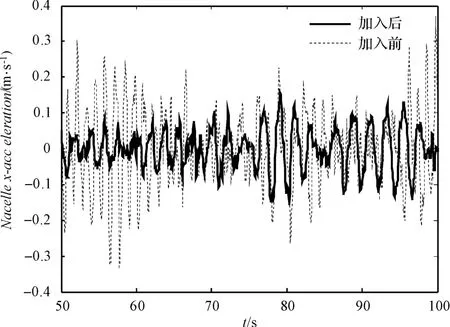
图3 机舱前、后x 方向加速度
3.2 等效疲劳载荷比较
等效疲劳载荷是评估振动对机构寿命损伤的有效方法[10],通过分别对策略增加前、后作等效疲劳载荷对比,可有效评价策略的减振效果。假设应力与载荷是成比例的,可以用载荷来代替应力。假设20年机组寿命中各部件载荷循环次数为1.83e8(cycle),根据IEC 标准规定,假设瑞利分布年平均风速为7.5 m/s。应用雨流循环计数法来表现疲劳损伤等效载荷。根据Miner 假设计算疲劳应力如下:
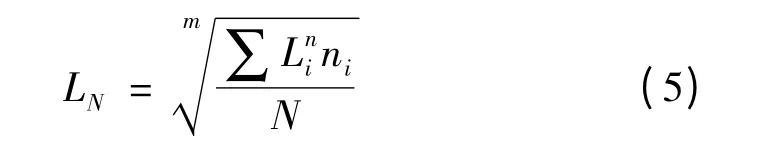
式中:LN—N 次循环等效应力幅,Li—在第i 个bin 的应力,ni—在一个应力变化幅度恒定时段内的载荷循环数,m—S—N 曲线的斜率,N—在机组寿命内允许的循环的次数。
利用仿真平台,取m=3,计算策略加入前、后塔底My的总疲劳载荷,其结果如表4所示。由表4 可知,塔架等效疲劳载荷明显减小。
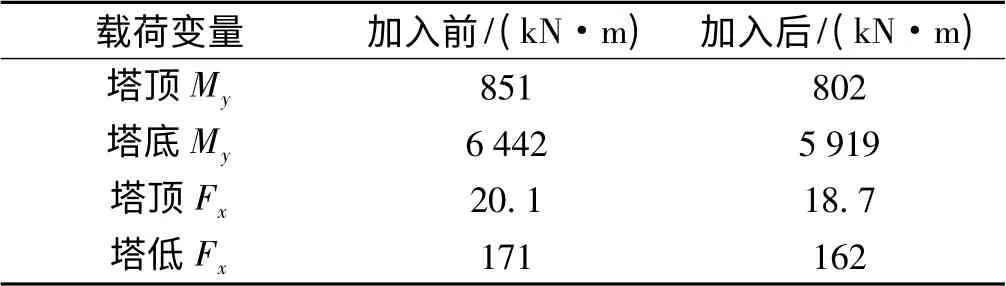
表4 等效疲劳载荷比较
3.3 风场实验风机验证
为验证减振控制的风场实际运行情况,本研究在张北国家风光储重点实验基地某实验风机上进行了现场测试。其中,1 个月的运行时间不加减振策略,另外1 个月加入相关策略。前、后振动峰峰值统计结果为:额定风速以上时段,加入减振策略后,前、后振动平均峰峰值为0.48 m/s2;不加的1 个月统计为0.61 m/s2,且不加减振策略的1 个月共造成2 次振动过大告警。
策略加入前、后在平均风速均为12 m/s 时的两段10 min 风场实时采样信号(合并在一张图中显示)如图4所示。由图4 可知,振动控制策略效果明显。
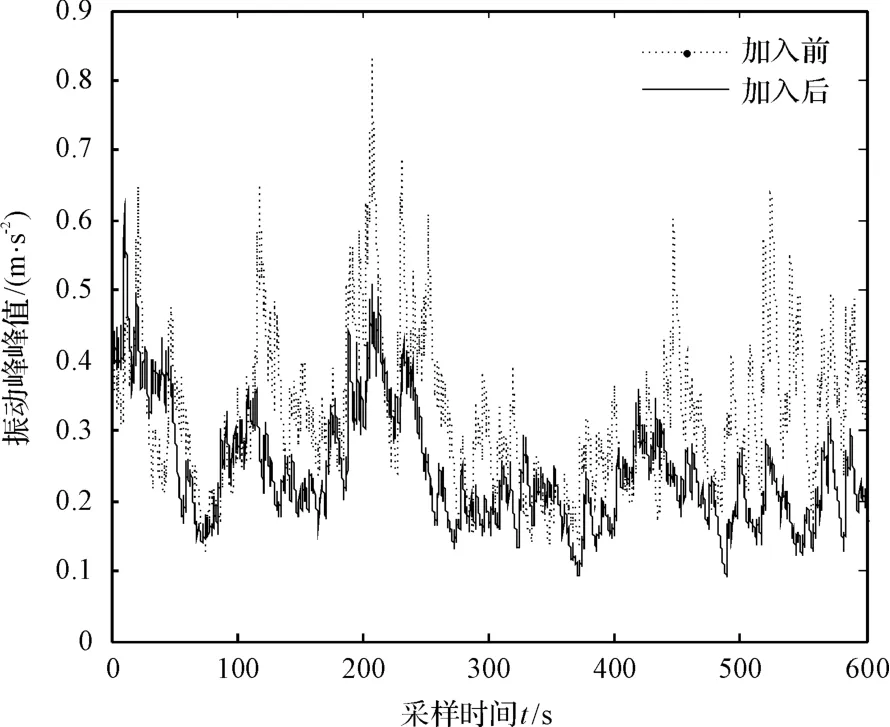
图4 塔架振动峰峰值
4 结束语
本研究通过对塔架振动原因进行分析,阐明了塔架主要激励源的特点,论证了塔架前期设计的优化点,并说明了塔架振动控制不能只依靠设计优化的原因,指出了运行过程中减振控制的必要性。基于上述分析,本研究做了以下研究,并得到了相应的研究结果:
(1)通过坎贝尔图分析得到了塔架的振动关注频率;
(2)建立了塔架的振动响应方程,在此基础上找到了控制塔架振动的理论基础;
(3)设计了塔架减振控制的传递函数,规划了减振策略;
(4)指出了减振策略的不足和应对方法;
(5)通过实验平台和当前正在风场运行的2 MW风机模型数据验证了策略的可行性;
(6)通过实验平台进行载荷计算,进一步验证了策略可行性。
研究结果表明,塔架加阻是必要的。数据分析结果表明,该减振控制策略可以减缓塔架运行过程中的振动值,提高风机寿命。
[1]刘 雄,张宪民,陈 严,等.水平轴风力机结构动力响应分析[J].太阳能学报,2009,30(6):804-809.
[2]周英华,郭廷福,蒋科杰.直驱型风力发电机组控制策略研究[J].机电工程,2013,30(3):354-357.
[3]胡国强.风力发电机组变桨系统的设计[J].机电工程,2012,29(5):588-592.
[4]邢作霞,大型变速变距风力发电机组的柔性协调控制技术研究[D].北京:北京交通大学电力系统及自动化学院,2008.
[5]王大为,陶学军,卢晓光.基于柔性叶片模型的独立变桨减载控制[J].电力系统保护与控制,2012,40(16):111-115.
[6]李本立,宋宪耕.风力机结构动力学[M].北京:北京航天航空大学出版社,1999.
[7]王朝胜,黄东胜,邹富顺,等.风力机塔架模态分[J].电力学报,2009,24(6):463-466.
[8]BURTON T,SHARP D,JENKINS N,et al.Wind Energy Handbook[M].England:Wiley,2001:486-489.
[9]BOSSANYI E A.GH Bladed Theory Manual[R].England:GH & Partners Ltd.,2009.
[10]FREUDEREICH K,ARGYRIADIS K.Wind turbine load level based on extrapolation and simplified[J].Wind Energy,2008(11):589-600.
