水锤波下简支管路的振动应力及疲劳寿命分析

樊泽明，曹 阳，梁振涛，傅殿玉

(1.西北工业大学自动化学院，陕西西安710129;2.沈阳机床(集团)有限责任公司，辽宁沈阳110041)

0 引言

飞机液压系统的管路振动问题多年来一直困扰着飞机液压系统设计师和事故分析人员。随着飞机液压系统的高压化，这一问题更加突出。飞机液压管路系统的故障失效，或者以支承结构损伤的形式出现，或者以固体管路断裂的形式出现。交变应力在航空工程中广泛存在，是造成破坏的重要因素。流体的脉动及外界的振动引起的管路交变应力容易导致疲劳破坏，一般认为这是造成管路系统故障失效的主要原因。但是在新机型设计之初，除了选择符合静强度和疲劳强度要求的支承结构材料及管路材料外，还要对管路系统进行必要的测试与调整，排除流体的脉动及外界振动引起管路系统疲劳破坏的可能性［1-3］。

管路的平面简支梁固定是一种典型的管路支承结构，地面试验常采用该方法固定管路。液压系统工作时，常伴随电磁阀的开关，在开关的瞬间将在管路内产生很大压力瞬变，这便是水锤波。对液压元件进行水锤脉冲试验，是新产品设计阶段的重要环节。为了准确测验出飞机液压管路的疲劳寿命，试验需要模拟管路所受到的振动和内部油液的压力脉动［4］。试验设备一般由振动台、一套能使试件实现简支的夹具、一套产生压力脉冲的油源系统等组成。基于此，本研究主要探讨水锤波下简支管路的振动应力及疲劳寿命。

1 管路应力计算

1.1 加速运动管路的应力

被测管路固定在振动台面上，可视为简支梁，管路的弯曲为纯弯曲。

试验夹具刚性地固定在振动台上，振动台通过台面把运动传给被测管路，使被测管路产生强迫振动。产生的振动形式为垂直方向的正弦振动，即简支梁的支撑点的运动轨迹为:

则加速度a 为:

在小挠度情况下，被测管路与振动台面运动相同。在t 时刻，管路做垂直方向加速度为a 的加速运动。

由材料力学可知，对于纯弯曲梁:

式中:Mx—x 点的弯矩，W—管路的抗弯截面系数。

对于空心圆截面:

式中:I—主形心惯性矩，D—管路外径，d—管路内径。

且:

式中:q—由重力和惯性力共同构成的均布载荷的集度。

q 与夹具给管路的力F 组成平衡力系，则:

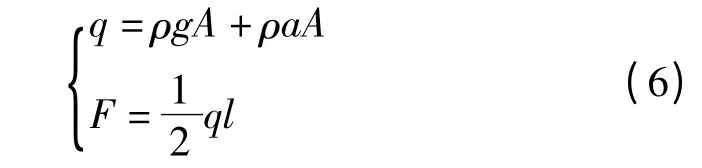
式中:ρ—管路密度，A—管路横截面积，g—重力加速度。

且:

综上，将式(4，5)代入式(3)，得:

由上式可知，对于简支梁，最大应力存在于梁的中部。

1.2 静压油液对管路应力的影响

实际试验时，要在管路内通入额定压力的油液。当管路振动时，管内液体也跟随管路做相同的运动。

对于管内液体，设qd为管路给油液在垂直方向上的均布载荷的集度，其值与油液的重力和惯性力组成的均布载荷的集度相等，故:

式中:ρ'—油液的密度，A'—油液的横截面积。

即:

则式(6)中的q 应更改为:

则纯弯曲的应力为:

通入油液后，除了振动产生的弯曲应力外，由油液对管路的内压产生的应力也不容忽视。其内压在管道径向均匀分布，设管路的内径为d，外径为D，中经为r，由弹性力学［5］可知:

式中:σr，σθ，σx'—油液对管路产生的径向应力、周向应力、轴向应力;P—油液压力。

可以看出，σr＜0，表现为压应力;σθ＞0，表现为拉应力;σx'与r 无关，沿x 方向分布的常量，表现为拉应力。

则x 方向的综合应力为:

2 管路应力的仿真计算

2.1 水锤波的数学模型

工程上采用的脉冲发生装置主要包括比例伺服阀、电磁换向阀、增压器、蓄能器及油源系统等。

水锤波发生装置可简化成如图1所示的数学模型。

图1 水锤波发生装置数学模型

图1 中，P0为额定压力，φ(x)采用二阶系统模拟，在一个水锤波周期刚开始时S1、S2闭合，在T/2 时刻S1、S2断开，则C(s)为近似的水锤波形。

二阶系统φ(x)为:

系统单位阶跃响应为:

由水锤波的压力迹线［6-9］，压力极限图中的超调量σ%为25%～50%，调节时间ts为0.15 T，由:

可得:

则可求得σ%，ts，系统模型参数如表1所示。

表1 模型的参数

2.2 仿真计算

固体管路的典型支承结构状态变化将对管路固有频率产生影响，支承刚度的下降将导致管路固有频率降低。仿真中假设支承结构具有足够的支承刚度，即管路系统的固有频率远高于流体管路系统脉动频率，忽略流体脉动压力对固体管路和支承结构的强迫振动产生的激励作用，不考虑流固耦合振动。

在外部激励下，管路将产生自由振动。试验中一般使振动台的振动频率与管路自由振动的固有频率相同以便于振动。简支管路自由振动的固有频率可由等效质量法、微分法等方法算出。即:

式中:E—管路的弹性模量，W—管路的截面惯性矩，M—管路与流体的单位质量。

工程上关心的是最低阶固有频率，即i=1 的固有频率。其中，一个周期内管路的应力变化如图2所示。

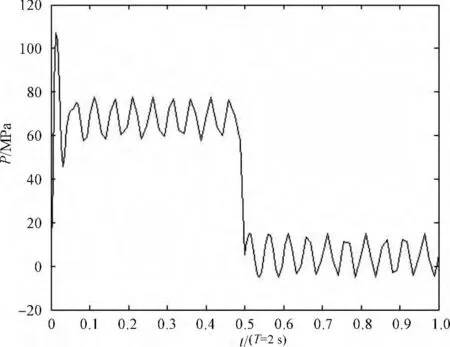
图2 T=2 s 单脉冲周期内管路的应力变化

仿真中取不同的压力脉动的周期，测量点为管路中点及应力最大点。仿真中相关参数如表2所示。

表2 相关参数

一般管路的固有频率远离外部激励信号即压力脉冲的频率，随着压力脉冲频率的增大，当频率接近或者与管路的固有频率重合，则将导致共振，在此状态下的管路将很快发生破坏。

3 管路的疲劳寿命估计

根据热力学原理，引入损伤驱动力Fd，上限值为FdH，下限值为FdL，Fdmax为周期循环中最大应力对应的损伤驱动力，则可将损伤演化速率表示为［10-14］:

式中:D—材料的损伤度，其相应的初始值为D0;N—循环次数;α，m，n—与材料相关的参数。

由式(19)可见，当Fdmax→FdL时，dD/dN→0，可认为管路不发生损伤演化;当Fdmax→FdH时，dD/dN→∞，可认为管路马上破坏。

试验中试件可认为处于单轴受力情况。对应于损伤驱动力上限和下限值的应变上限和下限分别表示为εdH和εdL，他们与初始损伤D0的关系如下:

式中:u，v—与材料相关的参数;εdH，εdL—初始无损伤的材料发生损伤演化所对应的应变上限值和下限值。

试验中，每个周期的应变峰值εdmax为恒定，则:

同时:

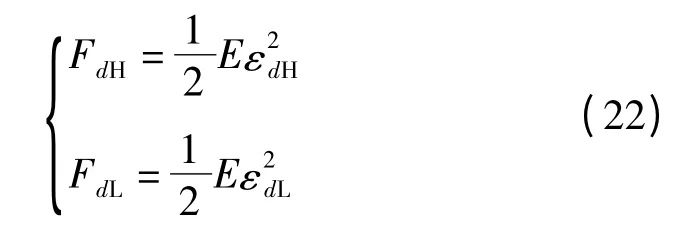
将以上两式代入损伤演化速率的公式，然后进行分离变量积分，可得到:

则管路从初始损伤到破坏的理论疲劳曲线方程为:

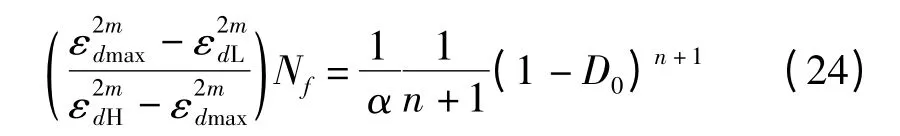
进一步，引入试验的最大应力σdmax，及应力上限值σdH和下限值σdL，即:

将以上两式代入理论疲劳曲线方程，得到以应力表示的且与初始损伤对应的理论疲劳曲线表达式:

可利用疲劳试验数据，应用最小二乘法拟合上述曲线方程，得到相应的参数。参数取值如表3所示。

表3 理论疲劳曲线表达式的参数

通过前面对水锤波下简支固定管路的应力的分析可得到在整个试验过程中液压管路所受的最大应力，而最大应力的周期即为水锤波的周期。下面分别对寿命与最大应力的周期及寿命与最大应力之间的关系进行仿真分析。

寿命与最大应力周期的关系如图3所示。

图3 寿命与最大应力周期的曲线

其中，图中最大应力的周期一定时，取10 Hz，寿命与最大应力的关系如图4所示。

图4 寿命与最大应力的曲线

由图4 可见，随着应力的增大，管路的寿命快速下降。当应力接近上限值时，管路将快速破坏。

4 结束语

本研究在详细说明了液压管路疲劳寿命试验的原理基础上，介绍了影响简支管路所受应力大小的因素，并推导了在外部装置施加振动及内部压力脉动双重因素影响下的应力公式，在不考虑流固耦合振动的情况下进行仿真，得到了寿命与应力之间的关系曲线，清晰地揭示了管路寿命与应力的大小和频率之间的关系，为液压管路选型计算、寿命分析及故障失效原因分析提供了参考。

同时该研究也存在一些不足，试验是在没有考虑流固耦合振动的情况下进行的，对于在流固耦合情况下的寿命与应力关系没有深入地研究，而流固耦合情况又是比较复杂的，所以下一步准备对整个系统做更加详细地分析，引入耦合因素，使试验结果更加精确。

［1］曹 源，金先龙，张晓敏，等.基于流固耦合的水力瞬变三维模拟及管壁动态应力分析［J］.振动与冲击，2009(11):70-72.

［2］丁丽华，刘 勇.振动作用下简支梁内残余应力的影响因素分析［J］.机电工程，1995，12(1):29-33.

［3］曹 源，金先龙，杜新光.水锤载荷作用下管道变形及动态应力［J］.核动力工程，2010(2):33-36.

［4］QU Yang，XIAO Ping，GAO Feng，et al.Modal analysis of the aircraft hydraulic-system pipeline［J］.Journal of Aircraft，2012，49(4):1168-1174.

［5］吴家龙.弹性力学［M］.北京:高等教育出版社，2011.

［6］赵孟文，袁朝晖，王鸿辉.高压力脉冲试验台设计［J］.液压与气动，2009(11):23-25.

［7］王 双，邓乾坤，张 斌.高压伺服控制脉冲试验台液压系统设计［J］.液压气动与密封，2012(9):21-24.

［8］李 军，陈 明.基于虚拟仪器技术的飞机液压脉冲试验系统［J］.测试技术，2007(3):77-79.

［9］袁朝辉，马 煜.基于PID 神经网络的液压脉冲试验系统［J］.液压与气动，2010(4):86-88.

［10］张 淼，孟庆春，张 行.无扩口管路连接件疲劳寿命预估的损伤力学-有限元法［J］.航空学报，2009(3):435-443.

［11］何慧慧，董金善，丁培丽.基于有限元的齿啮式快开压力容器疲劳分析［J］.轻工机械，2013，31(3):61-63.

［12］张 行.断裂与损伤力学［M］.北京:北京航空航天大学出版社，2006.

［13］周振龙，程光明.基于简支梁振动的主动控制技术研究［J］.机电工程，2011，28(4):418-421.

［14］HUANG Zhi-cheng，ZHANG Bai-qing，XU Han，et al.Study on the fatigue life of fully-automatic hydraulic press pull rods based on finite element and mechanical materials［J］.Advanced Materials Research，2012(58):70-73.