基于Leslie模型的中国人口红利期分析

■刘 鹏 博士生（北京大学经济学院 北京 100871）

引言

人口红利是指在人口年龄结构转变过程中，由于劳动年龄人口相对增加，老年人口和少儿人口相对减少，使劳动力人口抚养负担减轻，形成一个有利于经济增长的人口年龄结构。现阶段，我国正处于“人口红利期”，人口年龄结构中高比例的劳动年龄人口为我国的经济增长提供了有利的机会。但是，随着人口年龄结构的进一步转变，人口红利将最终可能转变为人口负债，阻碍经济的增长。

人口红利的概念是国外经济学家在研究“东亚奇迹”时首先提出的。Bloom和Canning在2002年进一步明确了人口红利的定义，即人口红利是指由出生育率、死亡率的降低导致人口年龄结构的变化，给发展中国家提供的有利于经济增长的人口机会窗口。

国内学者普遍认为我国目前正处于“人口红利期”并正享受“人口红利”带来的发展机遇，但在人口红利期的度量方面存在一定的分歧。彭希哲（2007）认为人口机会视窗将在2025年前后关闭，城市和东部沿海地区会关闭得更早。而蔡、王德文（2004）等认为2015年前后中国将到达人口红利的转折点。从此时起，劳动力开始负增长，人口老龄化加速将使人口转变对经济增长的贡献转为对经济增长的阻碍，即由人口红利转为人口负债。

中国“人口红利期”关闭时间的估算

Leslie矩阵人口预测模型是以年龄移算为基础的离散模型，能够较全面地考虑到影响人口总量与年龄结构的主要因素，可以比较精确地预测人口年龄结构的变化。本文通过运用Williamson（1959）的扩展后的Leslie矩阵人口预测模型，来预测未来不同年份我国各年龄段人口的变化，从而预测我国未来的人口抚养比的变化，确立“人口红利期”的关闭时间。

（一）扩展的Leslie矩阵人口预测模型

本文运用的人口预测模型基本形式为：

矩阵P(t+1)与矩阵P(t)分别代表时间t+1与t时的人口年龄结构矩阵，在矩阵P(t)中，Pi(t) 与qi(t) 分别为第t年年龄为i的女性个体数与男性个体数。M矩阵被称为Leslie矩阵，在M矩阵中：bi(t) 表示第t年年龄为i的妇女生育女性子代的生育率，di则为年龄为i的女性人口存活至年龄i+l的存活率。ai(t)为第t年年龄为i的妇女个体生育男性子代的生育率，ci则为年龄为i的男性个体存活至年龄i+1的存活率。

（二）模型假设

假设所有妇女均正常婚配且均会在育龄期（15-49岁）生育，不考虑多胎；假设所有人口都是自然死亡，不考虑天灾人祸等意外因素的影响；在模型预测期内，医疗卫生条件保持不变；不考虑国际人口迁移。

（三）M矩阵中主要参数的确定

存活率ci、di：假设在预测年份内男性分年龄存活率ci和女性分年龄存活率di与2000年人口普查的数据相同。

出生人口性别比xi(t)：分年龄段出生人口性别比xi(t)是指第t年年龄为i岁的育龄妇女生育的男性婴儿数与女性婴儿数的比值。

女性生育率ai(t)、bi(t)：结合中国统计年鉴分类标准，本文将育龄妇女界定为15-49岁的女性。

年龄别生育率fi(t)：是指年龄为i的育龄妇女在t年的平均生育率。计算公式为：其中，Pi(t)表示第t年年龄为i的育龄妇女总人口数，Fi(t)表示在第t年生育的年龄为i的育龄妇女总人口数。

总和生育率β(t)：是指一定时期各年龄组妇女生育率的合计数，说明每名妇女按照某一年的年龄别生育率度过育龄期，平均可能生育的孩子数。计算公式为：

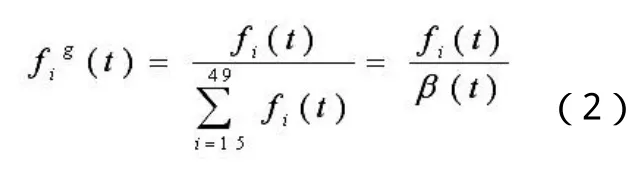
为保持与基础数据来源的一致性，本文采用根据2000年人口普查数据计算得到的年龄别生育率为规格化年龄别生育率，并用其表示未来年份里妇女的年龄生育模式。即：

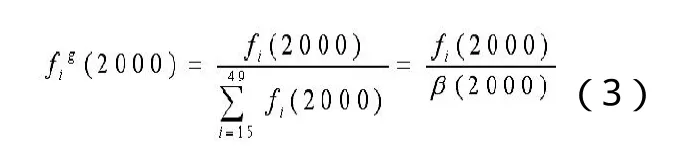
其中：fi（2000）为2000年年龄别生育率；β（2000）表示2000年总和生育率，可由公式（1）计算得到。

在确定了规格化年龄别生育率后，由公式（2）可以得到未来年份（2001-2050年）的年龄别生育率fi(t)与总和生育率β(t)之间的关系为：

因此，从公式（4）出发，通过在模型中设定不同的总和生育率β(t)，可以得到不同的年龄别生育率fi(t)，结合出生人口性别比xi(t)，可以得到育龄妇女生育男性子代的生育率，以及生育女性子代的生育率

为了考察不同的生育水平对人口抚养比的影响，本文设计3个不同的生育水平方案进行人口预测：

方案1——高方案：按照人口学的规律，总和生育率2.1是人口更替的一个平衡指标。因此本文的高方案将总和生育率设定为2.1。

方案2——中方案：本文的中方案总和生育率为1.8。

方案3——低方案：保持目前总和生育率1.4左右不变。

（四）模型预测结果分析

根据上述模型和设定参数，本文利用CPPS人口预测软件对2001-2050年人口分性别、年龄进行预测，然后加总得到总人口和各年龄段人口，进而推算出少儿、老年以及总人口抚养比。

1.总人口的变动分析。由图1可以看出三种预测方案下总人口的变动趋势。高方案：总人口将在增长到2048年的16.02亿峰值后开始稳步下降。中方案：总人口将在增长到2030年的14.71亿峰值后开始稳步下降。低方案：总人口将在增长到2021年的13.87亿峰值后开始快速下降。

2.人口年龄结构的变动分析。由图2可以看出三种预测方案下总人口抚养比的变动趋势。高方案：总人口抚养比在2008年出现拐点，随后逐步上升至2031年的52.6%后，开始进入人口负债阶段。因此，在高方案下，“人口红利期”的关闭时间为2031年。中方案：总人口抚养比在2009年出现拐点，随后逐步上升至2034年的51.8%后，开始进入人口负债阶段。因此，在中方案下，“人口红利期”的关闭时间为2034年。低方案：总人口抚养比在2011年出现拐点，随后逐步上升至2037年的52.6%后，开始进入人口负债阶段。因此，在低方案下，“人口红利期”的关闭时间为2037年。

通过图3对少儿人口抚养比的预测结果进行讨论。高方案：少儿人口抚养比在2050年上升至33.5%，仅仅上升了0.9%。中方案：少儿人口抚养比在2050年下降至25.7%，下降幅度为6.9%。低方案：少儿人口抚养比在2050年下降至17.8%，下降幅度为14.8%，相对中方案下降幅度更大。

由上文的讨论可知，除了高方案中少儿口抚养比有小幅上升外，其他方案中少儿抚养比都下降了，由此可知，在预测年份中，少儿抚养比的变动不会大幅度地引起总人口抚养比的上升，因此可以推断，少儿人口抚养比的变动不是“人口红利期”关闭的关键原因。

最后，通过图4讨论三种预测方案下老年人口抚养比的变动趋势，三种方案都表明我国老年人口抚养比将不断上升，而且上升幅度都较大，使得社会的老年抚养负担加重。高方案：老年人口抚养比的上升幅度为23.9%。中方案：老年人口抚养比的上升幅度为27.8%。低方案：老年人口抚养比的上升幅度为33.9%。

由此可见，老年人口抚养比的大幅度上升会引起总人口抚养比的上升，社会人口抚养负担逐渐加重，人口红利将会被逐渐抵消，向人口负债过渡。因此，老年人口抚养比的上升是我国“人口红利期”关闭的关键原因。

结论

首先，总和生育率是影响“人口红利期”关闭时间的因素之一。总和生育率越低，少儿人口抚养比越低，从而使总人口抚养比越低。根据本文的估算，如果继续保持总和生育率在现有的1.4的水平，中国的“人口红利期”将会在2037年关闭，享受的“人口红利期”在三种高方案中是最长的。但是，总和生育率越低，意味着少儿人口数量减少，未来的劳动年龄人口越少，将使社会面临更为严重的人口老龄化问题。

其次，人口老龄化是影响“人口红利期”关闭时间的关键因素。三种预测方案都显示我国老年人口抚养比将逐年上升，而且上升幅度相对较大，一方面老年人口抚养比的大幅上升，使总人口抚养负担逐年上升，逐渐吞噬现有的人口红利；另一方面也暗示我国要尽早做好应对人口老龄化深化的准备。

再次，适当的总和生育率有助于稳定未来的总人口抚养比。从预测结果看，一方面，较高的总和生育率，将在未来增加劳动年龄人口，因此适当提高总和生育率有利于缓解未来人口老龄化带来的总人口负担；另一方面，较高的总和生育率将导致少儿人口抚养比增加，进而加重总人口抚养负担。如果能综合考虑上述利弊关系，使总和生育率保持在适当的水平，将使我国在享受人口红利的同时，缓解人口老龄化等问题。

鉴于上述讨论，并考虑到我国庞大的人口基数，本文建议审慎放松计划生育政策，适当提高现有的总和生育率。

1.蔡.人口转变、人口红利与刘易斯转折点.经济研究，2010（4）

2.蔡，王德文.人口转变的储蓄效应和增长效应—论中国增长可持续性的人口因素.人口研究，2004（5）

3.陈友华.人口红利与人口负债：数量界定、经验观察与理论思考.人口研究，2005（6）

4.陈文权，赵滋，李得胜. Leslie修正模型在人口预测中的应用.世界科技研究与发展，2008（2）

5.周祝平.人口红利、刘易斯转折点与经济增长.人口学与计划生育，2007（6）