基于LabView2013实现FFT傅里叶变换

黄世瑜，施尚英

（四川职业技术学院，四川 遂宁 629000）

1 傅里叶运算

1.1 离散傅里叶变换（D FT）运算

有限长序列在数字技术中占有很重要的地位，主要原因是由于其频谱可以离散化.有限长序列的DFT本身可以完全表达序列的频谱，所以DFT也可以直接对信号进行频谱分析.设有限长序列x(n)进行离散DFT变化，其运算过程为：

计算一个X(k)的值需要N次复数相乘和(N-1)次复数相加；计算N点X(k)的值需要N2次复数相乘和N(N-1)次复数相加.又因为每个复数相加包括2个实数相加，所以，每计算一个X(K)的值要进行4N次实数相乘和2(2N-1)次实数相加，因此，整个DFT运算需要4N2实数相乘和2N(2N-1)实数相加.

从上面的分析看到，在DFT计算中，不论是乘法和加法，运算量均与N2成正比.因此，N较大时，运算量十分可观.例如计算N=10点的DFT，需要100次复数相乘，而N=1024点时，需要1048576（一百多万）次复数乘法，如果要求实时处理，则要求有很高的计算速度才能完成上述计算量.反变换IDFT与DFT的运算结构相同，只是多乘一个常数1N，所以二者的计算量相同.

1.2 快速傅里叶变换（FFT）运算

快速傅里叶变换（FFT）是计算DFT的一种快速高效的算法.FFT是离散傅里叶变换的快速算法，它是根据离散傅里叶变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的.

虽然FFT大幅度地降低了常规傅立叶变换的运算量，但对于一般的单片机而言，处理FFT运算还是力不从心.主要原因是FFT计算过程中的迭代运算是复数运算，要分开实部和虚部分别计算.

2 FFT主要应用

傅里叶变换是一种分析信号的方法，它可分析信号的成分，也可用这些成分合成信号.许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，傅里叶变换用正弦波作为信号在现代电子技术技术领域主要应用为：

2.1 信道调制与解调

正交频分复用（OFDM）是将信道分成若干正交子信道，将高速数据信号转换成并行的低速子数据流，调制到在每个子信道上进行传输.正交信号可以通过在接收端采用相关技术来分开，这样可以减少子信道间相互干扰ISI.每个子信道上的信号带宽小于信道的相关带宽，因此每个子信道上的可以看成平坦性衰落，从而可以消除符号间干扰。而且由于每个子信道的带宽仅仅是原信道带宽的一小部分，信道均衡变得相对容易.

2.2 语音信号处理

对语音信号进行FFT变换，将其从时域变换到频域，可以更加直观地观察它的频谱分布、宽度等信息，对进一步设计各种滤波器、编码及调制方式、识别模式等工作奠定基础.

2.3 图像信号处理

图像保存：通过FFT将图像分解为一组越来越小的正交归一图像，具有很高的压缩比仍能够将原始数据完全恢复而不引入任何失真.图像滤波：在进行FFT后，若在反变换之前对变换域进行选择，可对图像进行滤波处理.图像增强：正变换将一幅图像分解为大小、位置和方向都不同的分量，在逆变换之前改变域中某些系数的幅度，有选择提升需获取的分量，而忽略不需要的部分.图像复原：目标是对退化的图像进行处理，使它复原成没有退化的理想图像.

2.4 功率谱估计

在信号的功率谱估计中通常采用基于自相关函数的方法，而基于自相关函数的功率谱估计的结构与离散傅里叶变换非常类似.将其频谱分量所对应的参数加以调整和限制，使其与离散傅里叶变换输出完全一致，然后利用FFT算法来计算功率谱，从而实现功率谱的快速估计.

2.5 雷达信号处理

雷达信号处理算法中大多数采用FFT方法测量频率，如果提高测频精度需增加FFT点数，增加FFT点数的实质是在整个单位圆(即整个距离谱)上均匀增加频域采样点数，从而造成运算量的成倍增加。Chirp-z变换可以实现对回波频谱中的某段进行局部细化，从而在采样点数、运算量增加不多的情况下，大大提高雷达的测量精度.

3 基于LabView的FFT实现

在模拟电路范围，信号频率以Hz或mS来测量，但在数字系统中使用数字频率，它是模拟频率与采样频率之比，即

数字频率=模拟频率/采样频率，其单位为周期数/采样数

采用LabView的信号产生模板提供常用的信号发生器，从中找到正弦信号发生器，使其产生一个正弦信号.将此正弦信号输入到实数FFT.vi中的X端进行快速傅里叶变换处理，使时域信号转换为频域信号.然后经过复数至极坐标转换后将其显示出来。结构框图如图1所示.

3.1 前面板设计

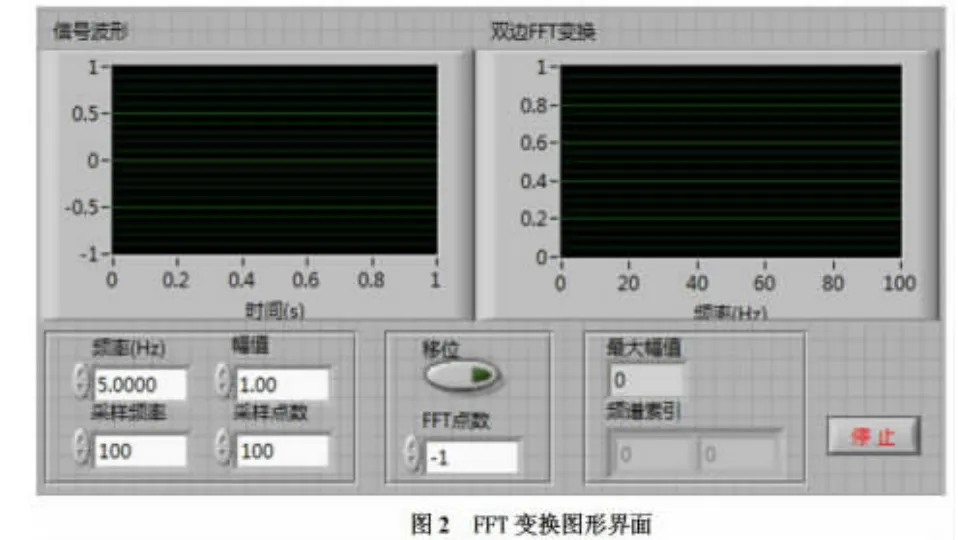
在LabView2013软件系统前面板设计中，主要实现正弦信号发生器频率、幅值、采样频率、采样点数等信号控制，变换后的频谱索引、最大幅值、图形等输出显示等.

建立两个波形图显示，一个作为正弦信号发生器产生的正弦波信号显示，即信号波形；一个作为变换后FFT信号输出图形显示，即双边FFT变换；添加5个数值输入控件实现频率、幅值、采样频率、采样点数、FFT点数控制；添加数值显示控件完成FFT最大幅值显示；添加数组性数值显示控件实现FFT输出频谱索引显示.

完成控件的布局调整与初值输入实现正弦信号双边傅里叶变换FFT图形界面设计，如图2所示.

3.2 程序框图设计

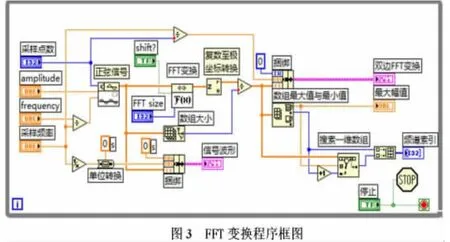
在LabView2013软件系统程序框图设计中，插入Whi le循环程序结构；正弦信号发生器、FFT傅里叶变换、复数值极坐标转换等VI模块；数组大小运算、单位转换、数组最大值与最小值、创建数组等函数.按图3所示FFT变换程序框图连接VI模块、函数、数据输入、数据输出及图形显示等完成FFT傅里叶变换程序设计.

3.3 程序运行

执行程序运行，如图4所示，在双边FFT变换频谱图中可观察到，频率为5Hz的正弦波经过傅里叶变换后，完成从时域到频谱上的映射，频谱上的最大幅值正好对应5Hz和95Hz.改变“频率”等输入控件的值，可以观察双边FFT变换频谱图最大幅值等输出参量变化情况.

4 结束语

基于LabView2013的FFT变化分析功能已经实现，在此基础上可加入高斯噪声发生器、滤波器等，可以模拟现代信号系统多数时域到频域变化过程.LabVIEW是一种功能强大的易学易用的操作简单的测试编程软件，可以通过本身自带的函数、模块等进行数据分析与处理，使用虚拟仪器开发FFT变化分析仪与传统的测量仪器相比，在开发周期、智能化程度、性能价格比、可靠性、可操作性、可维护性等方面具有明显的优势，可以省去购买硬件的费用，给系统集成和开发呆来极大的益处.

[1]岂兴明，田京京，夏宁.LabVIEW入门与实战开发100例[M].北京：电子工业出版社,2011.

[2]郑对元.LabVIEW虚拟仪器程序设计[M].北京：清华大学出版社,2012.

[3]黄松岭.虚拟仪器设计基础教程[M].北京：清华大学出版社,2011.