基于动态博弈技术优化配置数字图书馆共享资源模型

（宁夏农林科学院农业科技信息研究所，银川750002）

基于动态博弈技术优化配置数字图书馆共享资源模型

●谢静华,王银惠,王琛（宁夏农林科学院农业科技信息研究所，银川750002）

动态博弈；网络技术；资源优化配置；共享资源模型

从数字图书馆需求的角度出发，提出基于动态博弈技术来优化配置数字图书馆的共享资源，并构建出相关的模型。同时分析了动态博弈网络技术的特征、博弈机理、博弈方案，并介绍了有关的博弈方案和资源共享服务的辅助方式。

1 数字图书馆应用动态博弈技术关键点

在构建数字图书馆共享资源模型过程中，有三个关键链是博弈重点。（1）数据吞吐变化的信息是呈现不完全对称的。数据的瞬时变化震荡从整体上是不确定的，但在某些独立的数字图书馆节点又有一定规律可循。如各高校图书馆一天中下午、晚上是数据吞吐高峰；一年中5～7月是数据流吞吐高峰，但寒暑假期间数据流量几乎为零。由于数字图书馆的用户和时间具有的不确定聚集性，所以事件发展的信息对网络来说具有从模糊到清晰的过程。（2）根据不完全信息动态博弈的机理构建的数学模型评价指标主要包括网络的时延、时延抖动、吞吐量及丢包率等。［1］（3）应对方案要具有随时可调控的可操作性。数据吞吐的动态演变要求数字图书馆的后台数据调控机制必须满足在数据吞吐量及时延抖动出现剧烈变化时对数据并发数做出及时调整，避免造成数据冗余、用户使用障碍、网络瘫痪及后期维护负担。

2 数字图书馆的动态博弈调整实现

2.1 数字图书馆的动态博弈调整过程

数字图书馆使用网络动态博弈技术的技术核心是在个人用户、数据、用户需求、各个数据库、其他共享图书馆、数据点、服务设备网络吞吐量、时延抖动等相关要素出现动态变化时及时启动调控机制方案，对多地域、多用户、多类别的资源、数据进行动态调整，其目标是使应对方案在实施过程中随事件和环境的变化而变化。

以宁夏“三农”数字图书馆为例。根据保守统计，从2011年8月至2012年8月，宁夏“三农”数字图书馆点击率为1460214次，用户检索908869次，下载文献333391篇。

从2011年底开始，数据浏览、下载量就呈上升趋势，2012年2月、3月峰值最高。这是因为此阶段为科技项目申报期，下载量大于浏览及检索行为，下行的峰值数据速率压力增加。申报期过后，由于用户在申报项目后期会关注专业发展动态，因此浏览、检索量仍保持在5万次左右，而下载量只有高峰期的1/3左右，浏览、检索行为多于数据下载，要求网页数据快速响应。

运用“动态博弈”原理，随着上述各信息不断变化或者说逐渐完全的n个阶段状态，根据当前所掌握的不完全信息，对事件进行评估，针对可能出现的结果，选择那些便于下一阶段进行调整的方案。再复杂一些，如果每个应对方案是由若干项措施组成，就需要利用动态博弈机制将各种应对方案的措施进行重新组合，形成一个新的应对方案，使得整个体系中的各节点在实施过程中能够随变化进行技术或服务方式的调整。

2.2 动态博弈机理

由于采用动态博弈技术来优化配置数字图书馆的共享资源的预案参数是资源量的吞吐速率，它是数据分布状况、数据调用开始时间、调用持续时间、数据并发数的状态、数据并发数的有关属性（如密集使用的特定时间、地点、数据并发数指向的特定分类等）的参数，将其简化为数据保障率（G）。

资源调配机制与数据并发数进行博弈的目标是及时控制数据并发数并使损失最小。实际工作中，数据并发数据是动态变化的，因此数据吞吐调配机制的策略关键就是从方案空间中选择一个方案，使得保障率G在区间内最大。总体来说，震荡承受区间最优方案的判定标准应该是：该方案是在数据吞吐变化不确定性发展状态下，满足一定保障率约束，同时使得成本最小化的应对措施。

3 博弈方案［2］

（1）建立动态博弈模型的前期准备。设定数字图书馆数据库经历瞬时变化震荡承受区间，首先要设计有效的信息流机制，包括建立计算机网络、实现代码共享、统一管理制度等。一旦需要，这些就能迅速地将分散在各地的数据有机的组合，形成能够统一调动的有序数据，同时能够有力地保障资源调用渠道的畅通。

（2）建立动态博弈模型的构成要素。动态博弈模型的构成要素为资源调配机制和数据并发数。

（3）建立动态博弈模型的策略空间。数据并发数：假设数据并发数中只有两种可能的状态S1、S2，则状态空间为且S2＞S1，数据并发临界点之间的转移概率为Pij（ij=1，2）。

本研究通过3个子研究，验证了近邻信任可以减少低收入群体的短视行为。该研究结果与Jachimowicz等人(2016)在美国社会验证的社区信任可使穷人更偏向远期决策的结果基本一致，使其在中国社会背景下得到支持。同时，有关社区治理的案例研究发现，有效的社区治理可以减少贫困，使居民不过度消耗环境资源，做出更加利于长远发展的远期决策，而邻里之间的信任便是使社区治理机制有效运作的关键因素之一(张捷，2013)，侧面支持了研究结果。

假设资源调配机制只需在一定的时间之内（本例中假定为2个时间半径）以及一定的数据并发临界点状态下（S1，S2）将足够数量的资源D调配到并发事故点（设为X），出现状况有两个，一是达到资源调配机制的目标，二是只能在部分程度上控制数据并发事故状态（0%＜G＜100%）。资源总量D与保障率G之间的关系见表1。

表1 资源总量与保障率之间的关系

假定现在有四个数据节点玉、Ⅱ、Ⅲ、Ⅳ，它们距目的节点的距离（定义r为时间半径）如下图所示。

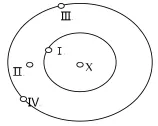
图数据点示意图

通过图示可知，玉在一个时间半径之内，Ⅱ点位于一个时间半径至两个时间半径之间，Ⅲ、Ⅳ两点都是恰好距离X点两个时间半径。

（4）建立动态博弈模型方案。假定各资源节点的总数量D以及运送一定数量的资源R到数据并发临界点X的成本见表2。

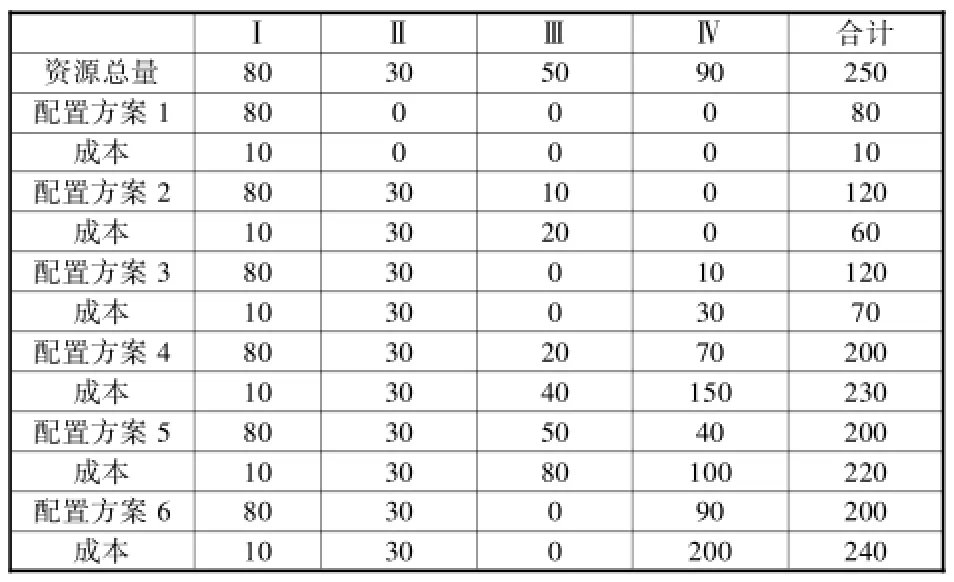
表2 数据存放量和运送成本数据

假定资源调配机制与数据并发数之间进行两轮博弈，以一个时间半径为一个博弈阶段，通过博弈得出一个博弈空间S。

设X点出现时延抖动剧烈事故，资源调配机制启动，从最近的玉点调配80单位的资源R到X点，将该方案记为甲；在方案甲实施中，事件继续发展进入第二阶段，调配机制方案有两类选择，即①从Ⅱ、Ⅲ、Ⅳ三点调配40单位的资源到X点，使其累计资源总量达到120单位；②从Ⅱ、Ⅲ、Ⅳ三点调配120单位的资源到X点，使其累计资源总量达到200单位。

根据表2所示，第一类方案又可以包括两个子方案（方案2和方案3），累计资源总量都可达到120单位，差别是方案2的成本较低。因此选定方案2，在方案空间中记作乙；第二类方案又可以包括三个子方案（方案4、方案5和方案6），累计资源总量都可达到200单位，成本最低者为方案5。因此选定方案5，在方案空间中记作丙。

假定资源调配机制决策目标以期望成本最小为决策准则，同时博弈结束后预期保障率达到100%，如果没能达到预期目标，则须进行弥补，但弥补成本较高，假定1%的保障率=20的弥补成本。则方案空间内的期望成本E有：

通过上述计算，利用动态博弈模型生成的预案如下：

（2）数据并发数应急事件发生，且状态特征为S2，则最优策略是在第一阶段选择方案甲，第二阶段选择方案丙。从玉点调配80单位的资源R到目标点X；同时着手实施方案丙，Ⅱ、Ⅲ、Ⅳ三个资源节点分别调配30、50单位和40单位的资源分担目标点的数据流量和服务的压力；预期能够在2个时间单位内将事件完全控制住，满足用户需求。预期总成本为220。

4 共享资源优化配置模型

数据上行下载的动态变化特性决定了在数据配置的同时必须考虑数据量的动态变化不是平衡的也不是稳定的，而是由当前状态向另一类或更深一级的动态变化发展的可能性，因此进行数据调配的动态调整，最终保证数据的有效利用，达到合理处置数据吞吐瞬时变化震荡的目标，这就是基于动态博弈网络技术思想下的数据优化配置。

4.1 布局重点

应急管理中的数据布局问题包括数据点的选址和配置两个部分，力图解决的问题就是数据点的设置，即数字图书馆共享节点的选择。选择哪个省、哪个图书馆作为数据资源的节点、配置什么专业的数据、数据规模等，目的是使数据的供应量达到最大或最优。节点布局问题具有四个基本要素：用户、设施、空间设施（离散型网络）、用来表示用户和设施之间距离大小或时间长短的度量（设置权重的距离或时间）。［3］

4.2 布局的模型［4］

模型以一个城市作为研究区域，并划分为多个待服务的小区域，将小区域假设为一个个有不同需求的可能数据调用高峰。第一数据调用高峰发生时，对数据的需求函数取决于数字图书馆数据调用率即数据的供应效率。简单情况下，假设一旦某个可能数据调用高峰发生，由两个点调配数据就能够应对，我们将从两个节点调用资源的过程视为两个阶段，两个阶段数据的数量分别构成一个组合。在两个点位置已确定的情况下，两个阶段数据调用高峰对数据的需求量是两个点到被供应点距离的增函数，第二阶段数据调用高峰对数据的需求量将是第一阶段对其数据供应量的减函数。为了使区域内数据总量调配最小化，就需构建各个点的最优数据配置议案。

假设研究区域中有n个数据点L1，L2,…,Ln，m个数据调用高峰H1，H2，…,Hm。

Ri：各数字图书馆可以提供共享的资源量（i＝1,2，…,n）；

Rij：表示资源R从两个资源调用点分别调配不同资源到同一个目标点的资源量（i,j＝1,2，…,n）；

Ti、Tj：节点i和j调用资源到目标点所花费的时间。

其中，各节点所调用的资源数是决策变量，数值是随与之相关量而变化的。一般而言，Rij是Ri的减函数，调用量总是小于总量的，同时Rij又是Ti、Tj的增函数，这源于调用时间会随着调用量的增加而增加。表示为：

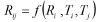
首先Ri是确定的，那么对于数据需求高峰Hk，得到一个矩阵Zk，其变量为，它表示对于该数据需求高峰来说，第一阶段从节点i调用资源量，第二阶段需要从节点j调用资源。由于的取值可能不同，因此每个元素实际上是多种组合（假设组合数均为1）的集合：

数据节点i、j分别调用的资源组合，都能够满足该资源调用高峰的需求。矩阵的对角线元素表示这两个阶段不能从同一个节点调用资源。该矩阵为满足资源调配高峰需求的数据组合矩阵，其形式如下：

对各资源节点的资源进行优化，使得整个研究区域数据保障率最大，所需要的资源总量最小，即满足。

约束条件是数据的配置应满足各数据调用高峰对数据的需求，即求（R1，R2……，Rn），使得对于每一个数据组合矩阵Ak，至少存在一个组合，其资源量小于或等于源节点付出的资源量，即，，使得。

对于每个数据调用高峰，都有类似的约束条件。将所有约束条件组合在一起，与目标函数构成一个0－1规划，该模型即为两阶段数据调用过程的数据布局模型。再利用分析定界等数学方法进行求解。所得（1,2,…n）即为各资源节点应付出的资源数量。

5 结论

当某个数据调用高峰发生时，数据吞吐变化是不确定的，这与很多因素有关，有时调配单个或两个节点的资源量并不能满足需求。本文研究的只是局部的两阶段数据调配预案，在实际工作中，有必要考虑如何对整个研究区域的资源进行合理布局的问题。因此，在数据布局过程中，将模型推广到多阶段的情况，合理采用数学方法是非常必要的。

［1］郭丽丽．博弈论在应急管理资源配置中的应用［D］．北京：北京交通大学，2007.

［2］姚杰，等．突发事件应急管理中的动态博弈分析［J］．管理评论，2005（3）：46－50.

［3］张茜．公共危机管理系统研究［D］．武汉：武汉理工大学,2006.

［4］贾传亮，等．基于多阶段灭火过程的消防资源布局模型［J］．系统工程，2005（9）：12－15.

［责任编辑］徐娜

G250.76

A

1005－8214（2014）07－0074－04

谢静华（1963－），男，宁夏农林科学院农业科技信息研究所图书馆馆员，副馆长；王银惠（1965－），女，宁夏农林科学院农业科技信息研究所副研究员；王琛（1973－），女，宁夏农林科学院农业科技信息研究所副研究馆员。

2013－08－02