基于三维CST建模方法的两层气动外形优化策略①

粟 华，龚春林，谷良贤

(西北工业大学航天飞行动力学技术重点实验室，西安 710072)

0 引言

几何外形参数化方法在飞行器气动外形设计优化中扮演着十分重要的角色，参数化外形不但需要提供足够的复杂度来保证对设计空间的探索能力，同时还应尽可能地减少设计参数，以快速搜索整个飞行器设计空间［1－2］。因此，气动外形参数化方法的选择需要同时考虑外形描述复杂度、设计空间规模和计算时间的影响。目前，飞行器的气动外形优化主要基于参数化CAD 几何模型［3－5］，庞大的建模平台、缓慢的运行速度和设计后拓扑无法改变的缺陷，使其在早期的概念设计阶段实用性不高;解析参数化建模方法通过解析函数形式描述飞行器气动外形，具有快速稳定、调节能力强的特点，非常适合于概念设计阶段的气动分析和优化，近年来得到了大量的研究和应用［6－9］。

类别/形状函数变换(Class Shape Transformation，CST)参数化方法是波音公司的 Kulfan［10－11］提出的一种基于类别/形状函数描述形式的解析气动外形建模方法，文献［12－14］对CST和其他参数化方法进行了比较。研究表明，CST方法具有设计参数少、适用性强、建模精度高等特点;Marco Ceze［15］对CST方法的设计参数特性和优化性能进行了研究;Michiel［8，16］提出了改进的CSRT方法，在CST基础上增加B样条函数来实现体积约束能力，并将其推广到三维机翼优化;Arash Mousavi［13］、关晓辉［17］、徐亚峰［18］等也分别使用CST方法实现了对翼型和机翼的设计优化;张珍铭［19］通过对CST方法引入机身截面宽度和高度沿纵轴方向的分布规律，实现了X-33高超声速飞行器三维气动外形的建模和优化，但其分布规律过于复杂，不具备通用性，难以描述复杂的飞行器外形。

受到飞行器几何外形复杂度的限制，当前基于CST等解析参数化方法的气动外形优化研究仍以二维翼型或三维机翼为主，无法全面的优化整个飞行器的气动性能。本文对二维CST参数化方法进行扩展，采用B样条函数代替Bernstein多项式进行展开，并引入侧向轮廓描述函数，基于部件组合的思想，通过多组特征体组合建立连续光滑的飞行器三维几何外形，形成了一种新颖的通用复杂三维飞行器几何外形建模方法;同时，结合CST和B样条函数的参数化特点，引入两层设计空间分层优化思想，将飞行器设计参数划分为全局尺寸参数和局部调整参数两类，进行分层优化设计，以降低优化难度，并提高优化效率;最后，以X-33高超声速飞行器为例，对其进行应用。

1 三维CST参数化外形描述方法

CST参数化方法具有设计参数少、外形描述能力强的优势，但Kulfan提出的CST参数化方法只能描述二维或简单由二维拉伸的三维对象，这限制了其实用性和拓展性。本文在其基础上，将二维解析描述形式向三维拓展，结合部件组合的思想，给出一套三维飞行器几何外形描述方法，既能够提供足够的三维外形描述复杂度，同时还具有设计参数可控的优势。

1．1 外形截面定义

式中 ψ为归一化的单位侧向长度，ψ=z/Lw;Lw为截面侧向总长;ζ(ψ)为对应 ψ位置处的法向高度;ΔζN(ψ)为法向偏心距，表示截面ψ位置处的法向偏离距离;(ψ)和S(ψ)分别为类别函数和形状函数，N1、N2为类别函数的控制参数，对于对称截面有N1=N2。

假定N1=N2，不同的控制参数下得到的截面几何外形如图1所示。

图1 不同控制参数下的截面形状Fig．1 Section shapes of different control parameters

1．2 B样条形状函数

B样条函数通过大量的低阶贝塞尔曲线(Bezier)来近似高阶曲线形状，k次B样条函数中权重因子的改变只会影响周围k+1个控制节点，比Bernstein多项式具有更好的局部控制能力［16］。因此，采用B样条来表示形状函数S(ψ):

其中，bi，i=0，1，…，n 为权重因子;k 次(k+1 阶)的 B样条基函数是定义在节点向量T={t0，t1，…，tn+k+1}，ti≤ti+1上的分段多项式(ψ)为定义在分割上的B样条基函数，其值可用De Boor-Cox递推公式确定:

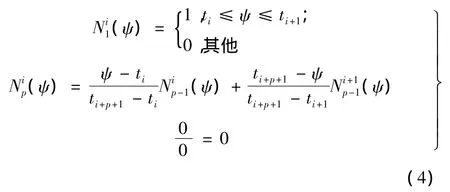
根据权重因子 bi(i=0，1，…，n)和节点向量T={t0，t1，…，tn+k+1}，ti≤ti+1，利用式(3)即可求出形状函数 S(ψ)。

1．3 三维CST描述方法

基于B样条形状函数得到的CST截面如下:

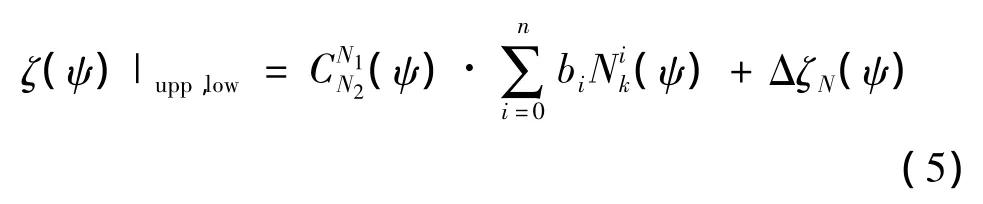
三维外形对象可看作一系列平行截面沿着轴线的组合。通过在不同的轴向位置处使用B样条形状函数描述不同的截面形状，确定出一个解析形状函数面，从而得到整个外形的解析描述形式。采用CST方法将式(5)中的bi沿轴线展开，定义:

其中，η=x/L，为归一化的轴线坐标;L为几何外形总长。

代入式(5)并展开:

式中 bi，j为飞行器上(下)表面的离散控制权重因子;n为截面侧向控制点展开阶数;m为轴向控制点展开阶数，此时的表面总控制点数为(n+1)×(m+1)。

实际上，式(7)中整个求和项即为二维B样条曲面的表达形式，因此产生的控制面具有类似B样条曲面的控制能力;当n=0，m=0时，可得到b=1，类似于二维情况，对应的形状函数S(ψ，η)=1，此时整个表面形状都由类别函数的控制因子N1、N2、M1、M2来控制;ΔζM，N(ψ，η)为对应(ψ，η)位置处的法向偏心距离修正项。

上述几何外形描述形式类似于在ψ×η的正交二维网格点中设计与其垂直的第三维坐标，从而表现出三维几何外形特征。ψ和η为单位化坐标，取值范围在［0，1］×［0，1］之间，无法描述侧向 ψ 的范围 Z 随 η的变化。因此，对Z引入同样的CST控制方式:

将上述定义转换到全局坐标系中，即可得到归一化的三维CST外形曲面的表达式:

式中 ψ =［0，1］;η =［0，1］。

整个三维CST曲面外形的设计参数包括:

轴向长度和侧向长度:L，Lw;

截面高度:LH1，LH2;

截面形状控制因子:N1，N2;

法向形状控制因子:M1，M2;

侧向形状控制因子:T1，T2;

表面权重因子:bi，j;

侧向权重因子:bt。

L、Lw和 LH1、LH2为外形尺寸参数。N1和 N2、M1和M2、T1和 T2为类别函数控制参数，当 bi，j和 bt取 1 时，即为最少控制参数情况;当bi，j和bt为参数矩阵时，相当于在外形表面上分布了对应矩阵维数的控制点。通过调节bi，j和bt的维数，即可实现控制参数的动态增减。

2 基于部件组合的通用飞行器建模

通过上述三维CST参数化方法，可得到光滑、连续的独立几何控制体，但单个几何控制体通常无法直接描述一个复杂三维飞行器外形。因此，引入部件组合的设计思想，将复杂飞行器外形拆分为一系列由三维CST参数化几何控制体组成的几何部件集合来描述。常用的几何构型部件包括头部、身部、机翼、尾翼，发动机等，通过上述几何控制体的相互组合，即可快速构建各类飞行器外形。

利用三维CST参数化方法，对基本几何外形构型进行封装，常用的构型组见图2～图4。将上述构型组相互组合，即可得到完整的飞行器几何外形布局。图5为使用三维CST参数化方法建立的可重复使用运载器X-34和高超声速民航机HSCT的气动外形。可看出，三维CST参数化方法具有很强的几何外形表达能力，结合部件组合思想，可快速、稳定地建立各类飞行器的几何气动外形。

图2 头身组合体基本构型Fig．2 Head-body basal configurations

图3 机翼基本构型Fig．3 Wing basal configurations

图4 尾翼基本构型Fig．4 Tail basal configurations

图5 三维CST参数化飞行器造型Fig．5 Three-dimensional CST parametric aircraft

3 两层设计空间气动优化策略

参数化几何外形的设计参数维数对气动外形优化设计空间和搜索效率有巨大的影响。过多的设计参数虽然增大了设计空间，同时也需更多的寻优时间，极端情况下甚至会造成优化算法收敛困难。因此，需对设计参数进行合理的筛选和分配。

通常情况下，可将气动外形设计参数划分为全局尺寸参数和局部调整参数。全局尺寸参数用于描述飞行器外形的轮廓尺寸，如机身长度、机翼展长等，主要用于设计初期大范围的气动外形寻优;局部调整参数用于对局部外形细节进行优化，如机翼截面形状等。三维CST参数化方法的设计参数包括外形尺寸、形状控制因子和权重因子3类。其中，外形尺寸和形状控制因子主要用于调整飞行器的基本轮廓形状和外形尺寸，与气动设计参数中的全局尺寸参数相对应;权重因子主要用于对外形进行全局调整或局部修正，对应于局部调整参数。

根据三维CST参数化方法的建模特点，将气动外形优化问题划分为两层设计空间优化问题。顶层设计空间包括外形尺寸和形状控制因子，用于实现对设计空间的大范围搜索;底层为权重因子 bi，j、bt，根据其维数大小，提供不同程度的局部控制和调整能力。两层设计空间优化能够在较好地保持原飞行器外形复杂度的同时，降低优化难度，并减少优化时间，从而提高气动优化效率。

两层设计空间按顶层到底层的顺序进行分层优化设计，基于三维CST建模方法的两层气动外形优化执行流程如图6所示。

图6 两层设计空间气动外形优化流程Fig．6 Aerodynamic shape optimization flowchart of two-level design space

4 应用实例

以X-33高超声速飞行器为设计对象，分别采用两层设计空间优化方法和常规的单层优化方法进行气动外形优化。X-33高超声速飞行器的气动外形基本尺寸如图7所示。建模时，将其简化为头身组合体、水平翼和双垂尾三部分。采用三维CST建模方法建立的X-33高超声速飞行器简化气动外形见图9(a)，其主要几何外形控制参数见表1。

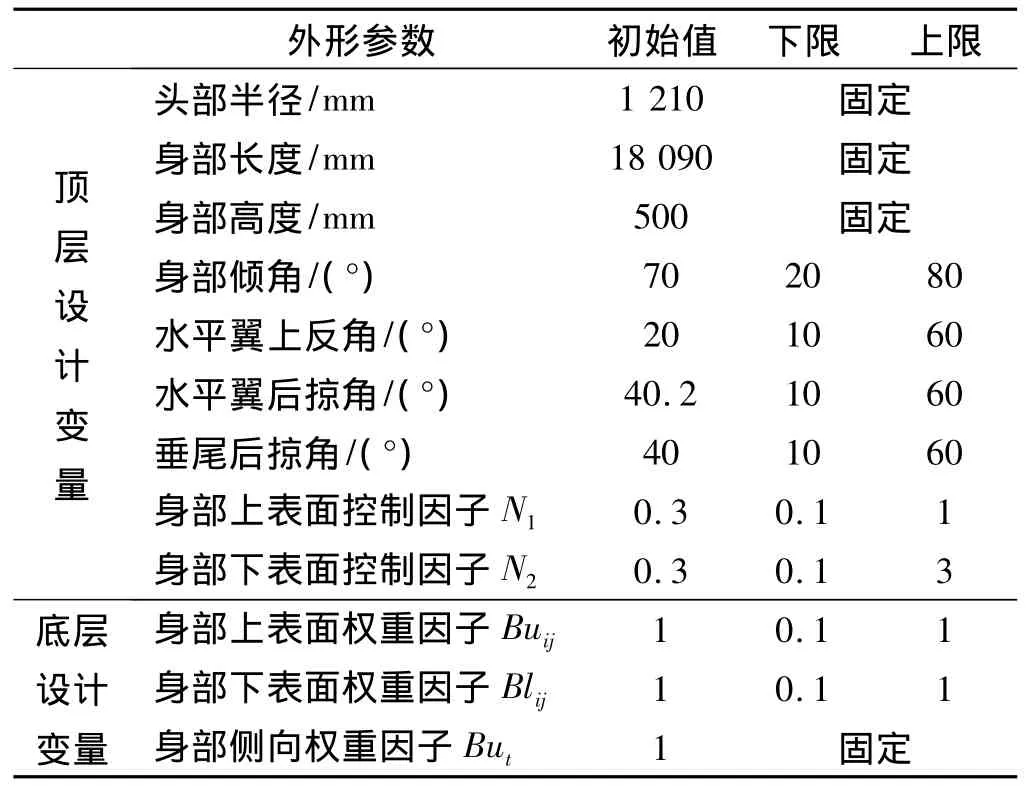
表1 气动外形控制参数Table 1 Aerodynamic shape control parameters

图7 X-33高超声速飞行器气动外形布局Fig．7 X-33 hypersonic aircraft aerodynamic shape configuration

采用基于牛顿流理论的面元估算方法作为气动分析求解器。其中，迎风面计算使用修正牛顿理论，背风面计算使用Prandtl-Meyer法，并引入基于参考温度法的粘性修正来考虑摩擦阻力的影响，面元估算方法的具体实现详见文献［20］。气动分析所需的面元网格通过直接离散CST参数化模型得到。

气动计算状态选择为Ma=6，攻角20°，为标准状态下X-33高超声速飞行器的最大升阻比点。此时，X-33高超声速飞行器的升阻比约为1．25，面元估算方法得到的升阻比为1．3。不同攻角下的升阻比和文献［21］中的试验数据对比如图8所示。虽然外形建模误差和气动估算精度带来了一定的计算精度影响，但升阻比的整体趋势和试验数据吻合较好。

图8 不同攻角下试验和估算升阻比对比Fig．8 Lift-drag ratio comparisons between experiment and estimation of different attack angles

以最大升阻比为优化目标，同时考虑容积利用率约束限制，X-33高超声速飞行器气动外形优化的数学模型如下:

式中 Cl/Cd为升阻比;X为设计变量，对应于表1中的顶层设计参数和底层设计参数;T为容积利用率;V为飞行器容积;S为飞行器表面湿面积。

选择序列二次规划算法SNOPT作为优化求解器，分别采用两层设计空间优化和单层优化2种方法进行X-33高超声速飞行器气动外形设计。其中，底层设计参数Bu和Bl都定义为［1×4］的参数矩阵，即在飞行器上下表面沿X轴方向各分布4个权重控制因子，其上下边界都设置为［0．6，1．5］。为保证气动外形平滑过渡，计算时对上述权重因子进行线性插值处理。

设计变量的最优值详见表2。两层优化中顶层设计参数优化后的最大升阻比为1．409，此时的气动外形见图9(b)，底层优化后的X-33高超声速飞行器的最优气动外形见图9(c)，最大升阻比达到1．429，比基准状态提高了9．9%，两层气动外形优化过程共花费1．85 h的优化时间;单层优化方法得到的升阻比为1．431，与两层优化的结果差距很小，但耗时长达10 h，单层优化的X-33高超声速飞行器最优气动外形见图9(d)。两层设计空间气动优化根据气动外形控制参数的特点，将设计空间划分为顶层和底层进行串联优化设计，合理地缩减了设计空间。相比于常规的单层优化方法，优化结果差异不大，但可显著地提高气动外形优化效率。

图9 初始和优化后的X-33高超声速飞行器气动外形Fig．9 X-33 hypersonic aircraft aerodynamic shapes on before and after optimization

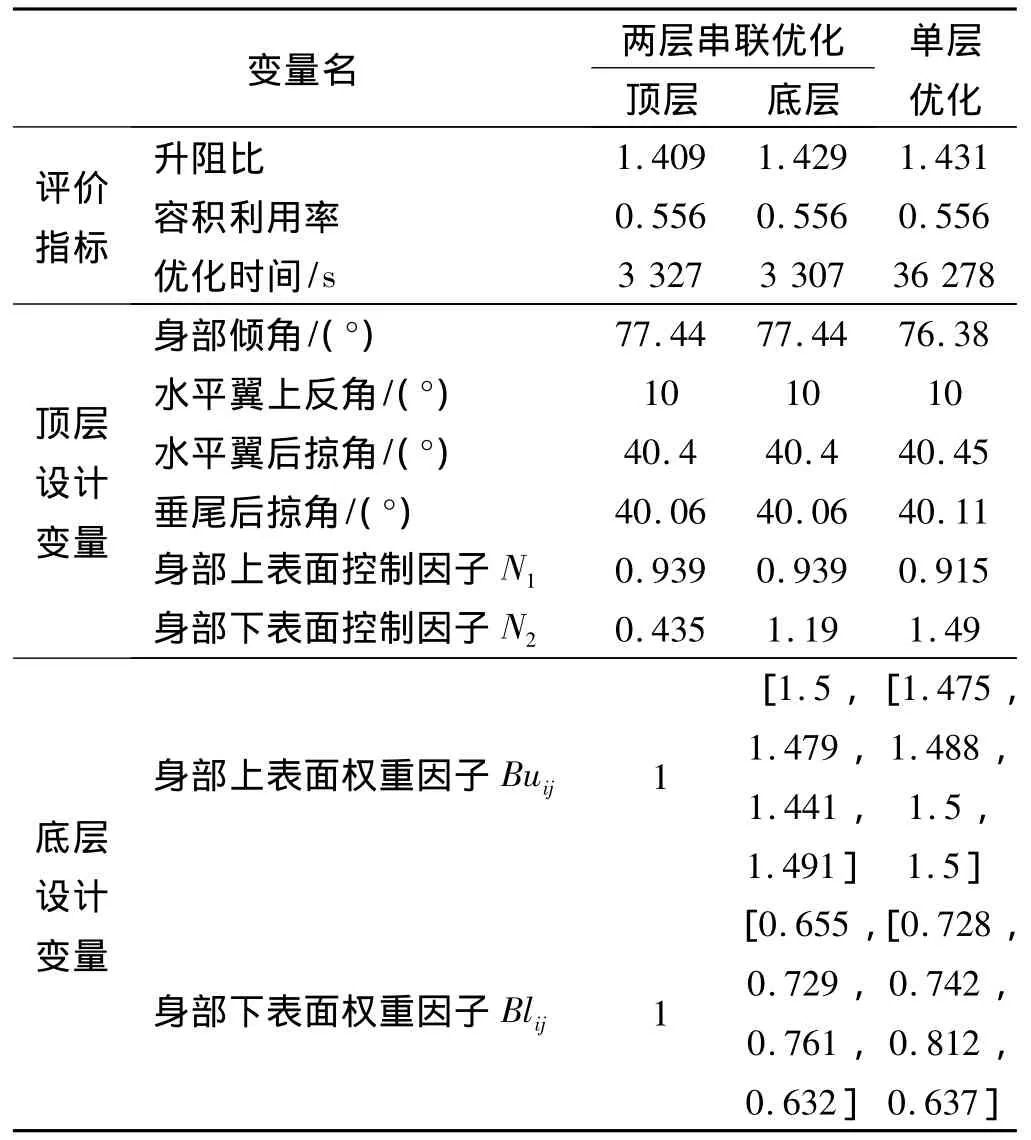
表2 两层优化与单层优化的优化结果比较Table 2 Result comparisons between two-level optimization and original optimization

5 结论

(1)提出了一种基于CST技术的通用三维飞行器气动外形建模方法，结合部件组合的思想，能以较少的设计参数，快速、稳定地建立各类飞行器的气动外形，具有很强的几何外形表达能力。

(2)通过增减B样条的权重系数维数，可快速、动态地调整飞行器气动外形的设计复杂度，从而适应于不同的设计阶段和设计目标。

(3)结合CST和B样条的参数化特点，建立了基于两层设计空间的分层气动优化策略。两层气动外形优化策略采用顶层优化-底层优化的串行流程，来实现优化过程;通过牺牲少量的设计空间，来达到快速优化求解目的。

(4)优化算例结果表明，两层气动优化策略的结果与单层优化的结果非常接近，但花费的时间远少于单层优化方法。因此，实际使用中，可通过两层设计空间气动外形优化，来达到节省优化时间、降低求解难度的目的。

［1］ Jamshid Samareh．A Survey of shape parameterization techniques［R］．MDO Branch NASA Langley Research Center，June 22-25，1999．

［2］ Frank H Gern．Improved aerodynamic analysis for hybrid wing body conceptual design optimization［C］//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition，09-12 January 2012，Nashville，Tennessee，AIAA 2012-0249．

［3］ Daniel M Fudge，David W Zingg．A CAD-free and a CAD-based geometry control system for aerodynamic shape optimization［R］．

［4］ Jamshid A Samareh．Geometry and grid/mesh generation issues for CFD and CSM shape optimization［J］．Optimization and Engineering，2005(6):21-32．

［5］ 金海波，丁运亮．飞机概念设计中的外形参数化模型的研究［J］．南京航空航天大学学报，2003，35(5):540-544．

［6］ Michiel H Straathof，Michel J L van Tooren．Development and implementation of a novel parametrization technique for multidisciplinary design initialization［C］//51st AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，12-15 April 2010，Orlando，Florida．

［7］ Rizzi J Oppelstrup．Coupling parametric aircraft lofting to CFD ＆ CSM grid generation for conceptual design［C］//49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition，4-7 January 2011，Orlando，Florida．

［8］ Kevin A Lane，David D Marshall．Inverse airfoil design utilizing CST parameterization［C］//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition 4-7 January 2010，Orlando，Florida，AIAA 2010-1228．

［9］ De Gaspari，S Ricci．A two levels approach for the optimal design of morphing airfoils［C］//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference 13-15 September 2010，Fort Worth，Texas，AIAA 2010-9388．

［10］ Kulfan B M，Bussoletti J E．“Fundamental”parametric geometry representations for aircraft component shapes［R］．AIAA 2006-6948．

［11］ Brenda M Kulfan．Universal parametric geometry representation method［J］．Journal of Aircraft，2008，45(1):142-158．

［12］ Jamshid A Samareh．Survey of shape parameterization techniques for high-fidelity multidisciplinary shape optimization［J］．AIAA Journal，2001，49(5):234-254．

［13］ Arash Mousavi，Patrice Castonguay，Siva K Nadarajah．Survey of shape parameterization techniques and its effect on three-dimensional aerodynamic shape optimization［C］//18th AIAA Computational Fluid Dynamics Conference，25-28 June 2007．

［14］ Sripawadkul V，Padulo M，Guenov M．A comparison of airfoil shape parameterization techniques for early design optimization［C］//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference，13-15 September 2010．

［15］ Marco Ceze，Marcelo Hayashi，Ernani Volpe．A study of the CST parameterization characteristics［C］//27th AIAA Applied Aerodynamics Conference，22-25，June 2009．

［16］ Michiel H Straathof，Michel J L van Tooren．Extension to the class-shape-transformation method based on B-splines［J］．AIAA Journal，2011，49(4):780-790．

［17］ 关晓辉，李占科，宋笔锋．CST气动外形参数化方法研究［J］．航空学报，2012，32(4):625-633．

［18］ 徐亚峰，刘学军，吕宏强．基于CST参数化方法的翼型快速设计［J］．航空计算技术，2011，41(5):24-29．

［19］ 张珍铭，丁运亮，刘毅．升力体外形设计的代理模型优化方法［J］．宇航学报，2011，32(7):1435-1444．

［20］ 粟华．再入飞行器多学科优化技术研究［D］．西安:西北工业大学，2010．

［21］ Kelly J Murphy，Robert J Nowak，Richard A Thompson，et al．X-33 hypersonic aerodynamic characteristics［J］．Journal of Spacecraft and Rockets，2001，38(5):670-683．