基于CFD的多级推力固体火箭发动机轴对称喷管型面优化与高精度性能预估①

陈 伟，梁国柱

(北京航空航天大学宇航学院，北京 100191)

0 引言

伴随着导弹武器系统对固体火箭发动机性能越来越高的要求，喷管的工作效率对固体火箭发动机性能的影响也就占有更加重要的位置。因此，如何高水平地优化喷管型面，特别是在现有喷管的基础上，如何进一步深入挖掘喷管的工作潜能，就成为固体火箭发动机设计的重要课题。

喷管型面的优化设计问题，首先要解决的问题是如何高效准确地预估喷管型面的性能和效率。早期的优化设计受计算能力的限制，大多采用计算量小、且模型相对简单(无粘流)的特征线方法［1］，而随着计算流体力学技术和并行计算技术的发展，现在越来越多的喷管型面优化研究是基于更为精确的直接数值求解N-S方程的 CFD仿真方法［2－3］。但由于 CFD方法复杂、计算量大计算稳定性差等问题，若不采取有效措施和策略，很难将CFD仿真方法和喷管的优化设计直接结合在一起。因此，如何能够高效稳健地基于CFD仿真方法来对喷管内型面进行优化设计，是喷管的优化设计中较为重要的课题。

本文将以较为常见的多级推力的固体火箭发动机为例，以CFD仿真为基础，探索合适的优化方法和策略，达到高效稳健和准确地优化设计喷管型面的目的，同时实现喷管的高精度性能预估。

1 优化对象和策略

1．1 优化问题分析

固体火箭发动机喷管内的流动由于摩擦、两相流等原因，使得喷管流动过程中存在各种损失，喷管实际比冲小于理论比冲。通过优化喷管型面，能降低喷管流动损失，提高发动机性能［4］。

多级推力固体火箭发动机相对于单级推力固体火箭发动机而言，其内弹道曲线和推力曲线呈阶梯状。如图1所示的双推力发动机的内弹道曲线，其中每个相对平稳的工作时间段称为工作段(图1中I和II)。多级推力的固体火箭发动机在导弹武器系统中是一种较为常见的发动机类型。例如，空空导弹的研制中，就广泛采用单室双推力的固体火箭发动机，因为双推力对应的导弹平均速度与末端速度都要比单推力大，性能更好［5］。由于燃烧室压力在不同的工作段各不相同，因此喷管在各个阶段的效率也各不相同，即使在某一个工作段喷管达到最优效率，往往其他工作段的效率就相对很低，整个工作段的效率更不可能达到最优。因此，需要兼顾各个阶段的喷管效率，才能使得喷管工作过程达到最优性能。而对喷管工作性能的评价，可采用CFD仿真方法来计算喷管内流场，从而通过分析流场的物理参数，来预测喷管的实际工作性能。

图1 典型的双推力固体火箭发动机的内弹道曲线Fig．1 Typical interior ballistics curve of dual-stage-thrust SRM

解决多级推力固体火箭发动机轴对称喷管的优化问题，首先要提取喷管型面的设计变量，建立CFD仿真模型;然后，通过CFD仿真方法预测多级推力固体火箭发动机各个不同工作阶段喷管的工作性能，综合各个工作段的喷管性能，预测喷管的总体工作性能;最后，通过优化算法优化型面的设计变量，使得喷管的性能达到最优。

1．2 仿真和优化策略

无论是CFD仿真计算，还是数值优化计算，都是通过迭代计算的方法来得到计算结果的，而基于CFD的优化就相当于嵌套迭代，其计算量相当于单独计算量的二阶放大。如果不采取措施，其计算量会达到难以承受的地步。另一方面，CFD仿真计算和数值优化计算都存在收敛稳健性问题，在很多情况下会出现迭代无法收敛的情况，而基于CFD仿真的优化，其收敛稳健性会变得更为脆弱。因此，必须采用合理的措施和策略，在保证计算精度和结果可靠性的前提下，减少计算规模，提高计算效率，且要保证计算的稳健性，提高计算的可靠性。根据本研究优化对象的特点，本文从CFD仿真模型、仿真方法、优化流程3个方面，来研究提高计算效率和计算稳健性的优化和仿真策略。

首先，从以下2个方面来简化CFD仿真模型，减少计算规模。

(1)将内弹道曲线分解，燃烧室压力在各个工作段上的变化较为平缓，可近似认为在各个工作段内为定常流。因此，采用定常流模型来进行CFD仿真，每个工作段的平均压强作为典型喷管入口压强进行仿真计算。

(2)固体火箭发动机喷管内流场多为气固两相流，但经过实践表明，采用两相流模型进行仿真的计算时间，往往是在相同条件下采用两相平衡流模型的计算时间的2～3倍，且两相流模型的计算稳健性要差于两相平衡流模型。因此，采用结合两相平衡流计算模型和两相流计算模型的方式来保证仿真精度，同时减少计算量和提高计算稳健性:优化前期，采用两相平衡流模型对喷管型面进行优化;然后，在两相平衡流的优化型面基础上，利用两相流模型对其进行修正优化。

(3)传统CFD仿真的一般流程是根据仿真对象建立2维或3维几何模型，根据问题划分网格，选择和配置CFD仿真模型，然后进行仿真迭代计算。这种方法并不适合于优化中的仿真计算，因为每次重新划分网格很难做到仿真的自动化，也无法保证网格的质量。考虑到本文研究的轴对称喷管是在其基本结构和工作状态大体已经确定的情况下的进一步挖潜优化，在各种几何约束的严格限制下，喷管型面尺寸参数可变的幅度已经很小。因此，本文采用了动态网格技术，在基本不改变网格规模的前提下，通过调整网格分布来适应新型面的方法，来处理每次的网格生成，使得每次新型面的仿真可采用前一次型面的流场数据作为仿真的初始值。由于每次优化中产生型面变化不大，流场改变很小。这样极大地减少了每次仿真的计算量，也大大提高了仿真计算稳健性。具体方法见第5章。

(4)由于各个工作段的仿真计算是相互独立的，因此可将各个工作段的仿真进行并行计算，提高计算效率。另外，在优化算法的选取上，各个优化算法的特点各不相同，有的收敛速度快，迭代稳健性差，而有的收敛速度慢，但迭代稳健性较好。因此，在本研究中，采用多个优化算法相结合的办法，在保证优化的稳健性基础上，尽量提高优化的收敛速度，减少计算量。

下面分别对仿真和优化模型进行具体阐述。

2 CFD仿真模型

2．1 基本假设

依据前文对CFD仿真模型的分析，做出如下假设:

(1)喷管内流场为二维轴对称定常流;

(2)燃气中的气相为完全气体，服从完全气体状态方程;

(3)忽略热辐射作用和化学反应，近似认为喷管内流动过程绝热;

(4)颗粒为均匀球体，颗粒是离散的，不考虑颗粒相的燃烧、蒸发、破碎及化学反应。不考虑由于颗粒相加速度产生的虚拟质量力，不考虑外部体积力和升力作用，不考虑颗粒相的体积分数变化湍流脉动产生的压力。

2．2 控制方程

采用Euler形式的二维轴对称有粘两相定常流的控制方程［6］:

连续方程为

pqq相的体积分数;ρp和ρq分别为第p相和第q相的密度。不考虑两相之间的传质现象。

动量守恒方程为

其中，Θs为颗粒温度;ess为颗粒碰撞恢复系数;g0，ss为颗粒径向分布函数。而对于气相，pq=0。

其中，s表示颗粒相参数;l表示气相参数;τs表示颗粒相微粒弛豫时间，定义为

阻力系数CD为

能量方程为

式中hq为第q相的比焓为第q相热流矢量。

注意到，若将式(1)～式(7)中固相的相应参数设为0，即可得到两相平衡流CFD仿真模型的控制方程。

采用较成熟的标准k-ε两方程湍流模型和重点区域加密的结构网格，以提高计算的准确性和稳健性。

2．3 仿真算法和边界条件

两相平衡流采用基于密度的隐式耦合算法，并选择二阶迎风的Roe-FDS格式作为数值离散格式。两相流采用多相耦合算法，即同时求解所有的方程来得到相速度和相间共享压力的修正值［9］，离散格式均采用一阶迎风格式。

入口边界条件为压力入口，其压力为各个阶段压力的平均值。对于两相平衡流，入口总温为燃烧室燃气总温。对于气固两相流，气相压力和颗粒相均采用两相平衡流的燃烧室燃气总温作为入口总温，而颗粒相的入口体积分数由推进剂颗粒相质量分数和气相与颗粒相的入口密度换算得到。

出口边界条件为压力出口，静压为其发动机工作高度的大气压，静温为室温。但由于喷管出口处为超声速气流，喷管出口的压力和温度由内部气流推断，而非边界条件上的压力和温度。当出口的局部压力低于边界条件的静压时，会发生回流现象，这时回流的压强和温度为边界条件的静压和静温。

另外，两相流颗粒大小采用质量加权平均经验公式和体积-表面积平均半径经验公式的平均值［10］:

3 喷管性能预估

在由CFD仿真计算得到的单个工作段的喷管内流场的基础上，通过对喷管的推力和质量流量进行积分，可计算出喷管工作的实际比冲，即

式中 Re为喷管出口半径;F为推力;为质量流量;Isi为第i个推力区间的喷管实际比冲。

因推进剂质量mi是给定的，则根据前面的假设，可得到发动机的实际总冲为

引入热力计算得到的喷管入口的燃气参数，可直接计算得到各个工作段不计喷管损失的理想比冲，并进一步计算得到理想总冲，即

由于喷管入口的燃气参数是给定的，因此计算喷管的总工作效率为实际比冲除以理想比冲，即

通过以上步骤计算得到喷管总工作效率η和实际总冲I指标，就可对多级推力的固体火箭发动机的喷管性能做出精确预估和评价。

4 优化模型

4．1 优化变量

喷管型面作为优化的对象，需采用一种描述喷管型面的方法来提取优化变量，本文采用分段线的描述法，即提取型面曲线上的特征变量。以图2为例，这是一个典型抛物线喷管，将其分为5段曲线，从中可提取7个相互独立的控制变量(其中，喷管的喉部直径由发动机确定的，而喷管入口由燃烧室结构设计所确定)，型面的其余变量包括喷管出口半径，可由这7个变量推导得出，如表1所示。

4．2 数学模型

优化的数学模型主要包含3个部分，即优化变量、约束条件和目标函数。

表1 喷管的控制变量Table 1 Control variable of nozzle

图2 抛物线喷管控制变量Fig．2 Control variable of parabola nozzle

优化变量:本文的优化对象是喷管型面，优化变量为4．1节所描述型面的控制参数x，即

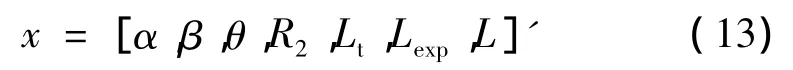
约束条件:喷管型面的主要约束包括结构约束和形状约束，结构约束包括发动机其他结构部分以及导弹/火箭结构的限制和约束，而形状约束主要是指喷管形状的几何合理性的约束，两者均为不等式约束，可表示为

目标函数:选择由式(10)得到性能预估指标实际总冲I作为目标函数:

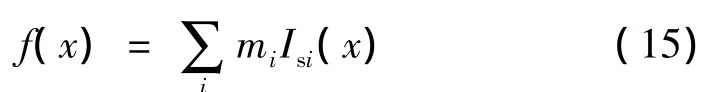
考虑到优化计算中一般以最小化目标，确定优化模型为

4．3 优化算法

本研究针对的喷管优化问题是非常典型的非线性有约束的线性规划问题。按照前述的优化算法的策略，本文选择了内点法(Internal Point)［11］和序列二次规划(SQP)［12］2种特点互补的算法完成该优化计算。内点法稳健性高，收敛性好，但收敛速度慢，而SQP算法收敛速度高，但易发散。优化计算前期，采用内点法，保证其收敛稳定性，在接近最优点时，切换成SQP算法，提高收敛速度。利用2种算法相结合的办法，提高收敛速度，保证了优化迭代的稳健性。

5 计算流程实现

5．1 动态网格生成

根据前文所述的策略，通过采用动态网格的方法，避免了每次重新对新型面进行CFD仿真，从而减少计算量、提高计算稳健度。

本文采用Thompson提出的椭圆型方程的结构网格生成方法［13］，在迭代初期，确定加密位置和网格总数，利用椭圆型方程结构网格生成法，根据新型面参数调整网格点分布，既保证了网格的相似性，也保证了网格适用于新型面。流程图如图3所示。

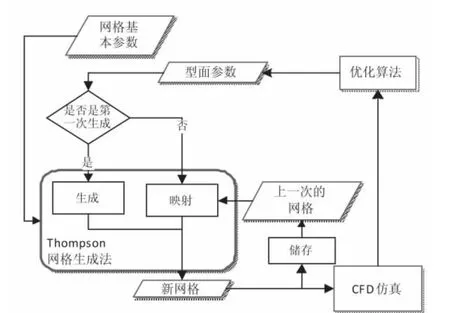
图3 动态网格流程图Fig．3 Flow chart of dynamic grid generation

每次优化迭代产生新的设计变量，通过新的设计变量，生成型面曲线，若是第一次生成网格，则由Thompson网格生成法生成新的网格进行CFD仿真计算。若不是，则通过Thompson网格生成法，在不改变网格总数和分布要求的基础上，按照新型面参数生成网格，将上一个网格的模型参数、算法设置、流场结果等映射到新生成的网格，使其仍能使用上一次仿真的流场计算结果。然后，将其导入到CFD，以上一次的流场分布为初始值，开始进行CFD仿真计算，实现CFD仿真数据的充分利用。

5．2 仿真并行化

虽然多级推力发动机的喷管在实际工作中的各个工作段是依次进行的，但由于将各个工作段的流场看成是定常流，因此各个工作段的流场是相对独立的，对其进行的CFD仿真同样是相互解偶的。因此，可采用并行化的方式，同时对不同工作段的流场进行CFD仿真。在生成网格后，分别导入不同工作段CFD仿真程序，按照不同的工作段的工况，分别设置不同的入口条件，之后就可同时进行仿真计算。这样充分利用了多核或多机的计算资源，提高了计算效率。

5．3 优化计算流程

按照图4的流程图，在Matlab平台上完成优化模型、流程控制和策略的实现，并通过成熟的商业计算流体力学软件Fluent平台搭建CFD模型，实现了最终的自动化的优化计算流程。

图4 优化计算流程图Fig．4 Flow chart of optimization calculation

6 结果和讨论

6．1 问题描述

以某空空导弹固体火箭发动机长尾喷管的优化问题为例，来验证方法的有效性。

该发动机是一两级推力的固体火箭发动机，长尾喷管的前长尾部分由于结构限制无法变动，需要对尾部的收缩扩张喷管进行型面优化，进一步挖掘工作潜力，提高喷管性能。

发动机喷管入口压力为两级压力，分别为8．798 MPa和 4．719 MPa。要求喷管长度保持不变，并受到发动机及导弹结构外形的严格约束，以此为约束条件，进行优化计算。工作高度为地面高度，环境压力为 0．101 325 MPa。

由于喷管的长度为固定长度，因此喷管的控制变量变为6个，即

6．2 计算结果

在8核Xeon计算服务器上，经过64次的优化迭代步，约54个机时完成了优化计算，得到了优化型面，如图5所示。与原型面和优化型面对应的性能预测结果和实际试验结果如表2所示。

其中，原型面喷管扩张段的二次曲线方程(原点为轴线上距出口138．35 mm处)为

对比优化型面喷管扩张段的二次曲线方程(原点为轴线上距出口140．4 mm处)为

图5 优化型面和原型面的对比图Fig．5 Comparison of optimized and original profile

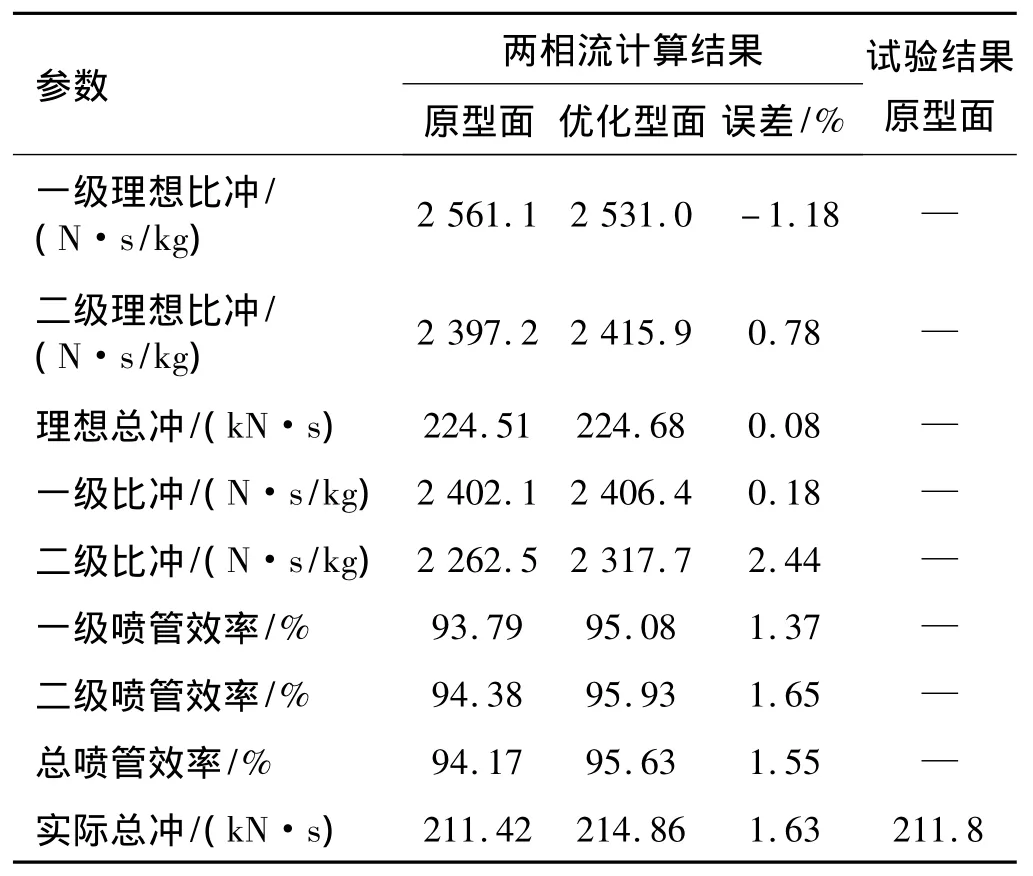
表2 喷管型面性能优化结果Table 2 Optimization result of performance for the nozzle profiles

根据表2的结果对比，对比原型面实际总冲预测值和试验实测值，误差只有0．18%，说明文中的CFD数值仿真模型的性能预测精度很高，喷管性能预测方法和结果可信。相比于CFD模型误差，喷管的总冲优化幅度达到了1．63%，其幅度远比仿真误差大，可认为优化是基本可靠的，优化结果是可信的。

总览图5和表2结果可知，原型面和优化型面从两方面提高了喷管的性能:

(1)从理想比冲和理想总冲的对比数据可知，通过调整喷管的扩张比，使得一级理想比冲降低，二级理想比冲增加，虽然二级比冲增加的幅度小于一级比冲，但由于二级工作段所消耗的推进剂质量更多，使得理想总冲有0．08%小幅提高，这说明了优化结果更好地平衡了喷管两个工作阶段的膨胀损失，减少了总的膨胀损失。

(2)从喷管效率的对比数据可知，通过优化型面曲线，减少了喷管的摩擦损失等非膨胀损失，使喷管性能提高了1．55%，是优化型面的性能提高的主要原因。

可看出，有效提高了喷管的总冲性能，达到1．63%，这对空空导弹的性能提升来说是十分重要的。

对比最终流场计算结果如表3和图6所示。从中可看到，一级和二级工况的边界总压(最低总压)都有显著提高，而总压的减少主要是由摩擦引起的，这说明优化型面相对原型面显著减少了喷管的摩擦损失。

通过对比两相平衡流和两相流的计算结果，可计算得到喷管原型面与优化型面的两相流损失，如表4所示。根据表2的喷管效率结果分别可计算出原型面和优化型面喷管总损失为5．83%和4．37%。对比表4的结果可知，优化型面相对原型面的两相流损失虽然有0．14%的增加，从颗粒相体积分数分布图可看到，如图7所示，优化型面沿壁面的颗粒分布更为集中，但相对喷管总损失的降低幅度1．55%，其影响很小。在该喷管的效率损失因素中，两相流损失对喷管型面改变的敏感性相对较低。这说明本文所采用的优化过程中，先后基于两相平衡流和两相流性能估算的分步优化策略是有效的，并在保证结果精度的同时，降低了计算复杂度，提高了计算效率。

图6 原型面和优化型面的静压分布Fig．6 Static pressure distributions of original and optimized profile

表3 喷管内最高与最低气相总压比较Table 3 Comparison of highest and lowest total pressure of gas phase in nozzle

表4 两相流损失对比Table 4 Comparison of two-phase loss %

图7 原型面和优化型面的颗粒相体积分数分布Fig．7 Particle phase volume fraction distributions of original and optimized profile

7 结论

针对多级推力固体火箭发动机的特点，建立了可靠的CFD仿真模型，对不同工作段的喷管内流场进行仿真，通过综合各工作段喷管内流场参数，计算得到发动机的实际总冲和喷管工作效率，实现了一种精确预估喷管性能的方法。

通过合理应用CFD模型、动态网格、并行化仿真等技术和策略，将基于CFD仿真预估喷管性能的方法用于喷管型面的优化设计中，解决了计算规模过大、计算不稳定等问题，能高效稳定、可靠地对多级推力的固体火箭发动机轴对称喷管型面进行优化计算。为固体火箭发动机设计人员深入地挖掘喷管潜能和提高喷管的设计水平，提供了切实可行和有效的方法。

考虑到基于数值仿真的优化设计方法的通用性，本文对探索其他部件或领域的基于数值仿真的优化设计计算方法也具有参考价值。

［1］ 方丁酉．两相流喷管扩散段型面优化计算［J］．航空动力学报，1986，1(2):137-140．

［2］ Cai G，Fang J，Xu X，et al．Performance prediction and optimization for liquid rocket engine nozzle［J］．Aerospace Science and Technology，2007，11(2-3):155-162．

［3］ Wang X，Damodaran M．Optimal three-dimensional nozzle shape design using CFD and parallel simulated annealing［J］．Journal of Propulsion and Power(0748-4658)，2002，18(1):217-221．

［4］ 李宜敏．固体火箭发动机原理［M］．北京:国防工业出版社，1985:308．

［5］ 刘海峰．单室双推力固体火箭发动机装药［J］．上海航天，1990(3):5-9．

［6］ ANSYS Inc．Ansys fluent theory guide［Z］．ANSYS Inc．，2009．

［7］ Lun C K K，Savage S B，Jeffrey D J，et al．Kinetic theories for granular flow:inelastic particles in couette flow and slightly inelastic particles in a general flowfield［J］．Journal of Fluid Mechanics，1984，140:223-256．

［8］ Wen C Y，Yu Y H．Mechanics of fluidization［J］．Chemical Engineering Progress Symposium Series，1966，62(67):100-111．

［9］ Ghobadian A，Vasquez S A．A general purpose implicit coupled algorithm for the solution of eulerian multiphase transport equation:international conference on multiphase flow［Z］．Leipzig，Germany:University of Florida，2007．

［10］ 杨丹．固体火箭发动机气-固两相流的数值模拟［D］．哈尔滨工程大学，2006．

［11］ Waltz R A，Morales J L，Nocedal J，et al．An interior algorithm for nonlinear optimization that combines line search and trust region steps［J］．Mathematical Programming，2006，107(3)．

［12］ Nocedal J，Wright S J．Numerical optimization［M］．2ed．Springer Verlag，2006．

［13］ Thompson J F，Warsi Z U A，Mastin C W．Numerical grid generation:foundations and applications［M］．New York:North-Holland:Elsevier Science Pub．Co．，1985．