基于轨迹线性化和自适应模糊系统的导弹自动驾驶仪设计①

肖 科，雷虎民，邵 雷，段朝阳，王 君

(1．空军工程大学防空反导学院，西安 710051;2．中国空空导弹研究院，洛阳 471009)

0 引言

轨迹线性化控制(TLC)是一种解决非线性、强耦合系统控制问题的新方法，在导弹、移动机器人和非最小相位系统等工程设计中得到广泛运用，且取得了良好的控制效果［1－2］。同时，许多学者利用模糊系统或神经网络的逼近特性，将轨迹线性化与模糊系统或神经网络相结合，以提高控制系统的鲁棒性［3－4］。但是，上述逼近过程不可避免地存在逼近误差，不能达到理想的控制效果。为消除逼近误差的影响，一般引入一个鲁棒补偿项。该补偿项的确定需要一个确切的最小逼近误差界，而该值无法直接测量得到，只能进行估计［5］。文献［6］采用直接假定最小逼近误差界的方法，这样可能会导致2种情况:一是估计值太大，使得控制律设计过于保守;二是估计值太小，导致控制系统失稳。文献［7］采用在线自适应调节的方法来估计最小逼近误差的界，合理、较好地解决了这个问题，且适用性更广。

本文研究了导弹系统的非线性、强耦合性和不确定干扰问题，设计了一种新的鲁棒自适应导弹自动驾驶仪。使用轨迹线性化方法解决快回路非线性和强耦合性，将系统不确定和外界干扰引入慢回路，继而用自适应模糊系统逼近慢回路动态模型，在最小逼近误差界未知的情况下，借鉴文献［7］的估计方法，设计自适应鲁棒补偿项。该自动驾驶仪能够消除系统不确定性和外界干扰对系统性能的影响。

1 导弹的非线性动态模型

考虑如下导弹的非线性动态模型:

由式(1)可知，导弹的动态模型具有很强的非线性和耦合性。根据时标分离原则，可以将导弹的非线性动力学模型分为快、慢回路。其中快变量为x1=［ωzωyωx］T，慢变量为 x2=［α β γ］T，快回路控制输入量为 u1=［δzδyδx］T，慢回路控制输入量为 u2=［ωzωyωx］T，与快变量 x1一致。f1(x1，x2)是关于状态量 x1和x2的光滑函数向量，f2(x2)是关于状态量x2的光滑函数向量，g1(x1)与g2(x2)分别为关于状态量x1和x2的矩阵函数。则导弹的快、慢回路的动力学方程可表示为

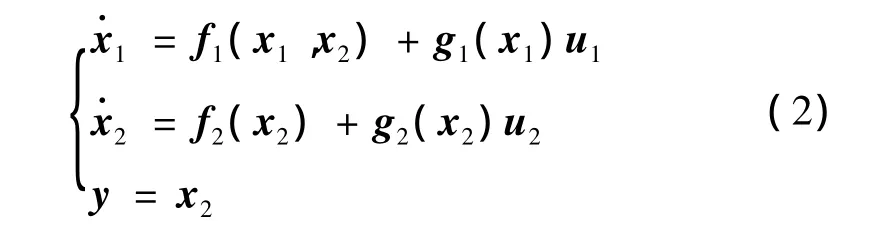
考虑建模时的误差和外界扰动，将式(2)改写为

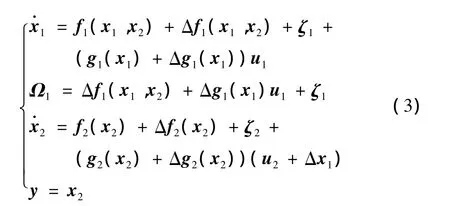
式中 Δf1(x1，x2)、Δg1(x1)和 Δf2(x2)、Δg2(x2)分别代表快回路和慢回路中因参数摄动所导致的不确定性;ζ1、ζ2分别为快回路和慢回路中的外部扰动;Δx1代表快回路中的总的不确定作用量Ω1对造成的影响，并在慢回路中体现。

2 快回路轨迹线性化控制器设计

文献［7］采用动态逆方法对快回路进行控制，迫使快变量的变化率快速跟踪控制指令的变化，而忽略快回路中的参数的摄动和外界的扰动对快变量的影响，将参数摄动与外扰归入慢回路进行处理，削弱了系统的鲁棒性。因此，本文采用轨迹线化方法对快回路进行控制，既能快速跟踪控制指令，又能减弱快回路对慢回路的扰动。

快回路动态模型:

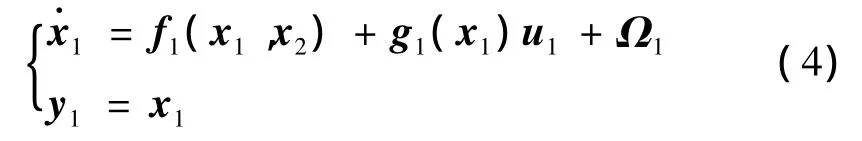
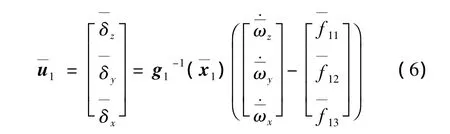
其中，x2(k)为快速跟踪微分器的微分输出;r为跟踪因子，且r越大，其跟踪速度越快。其余相关参数含义详见文献［9］，在此不再赘述。

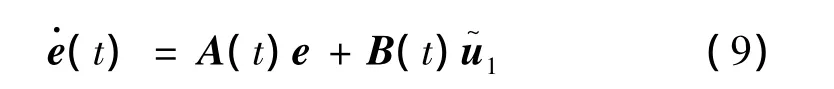
其中，

利用微分代数谱理论设计状态反馈控制律［2］:

闭环跟踪误差方程:

由此得快回路标准TLC控制律:

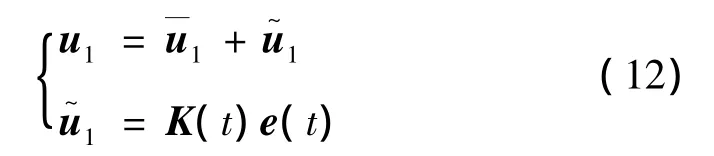
由文献［10］中定理4．13可知，线性时变反馈控制律(10)可保证非线性系统(8)在平衡点e(t)=0处指数稳定。根据扰动系统理论［10］，当模型误差‖d‖较小时，TLC控制律可保证快回路跟踪误差有界。

3 慢回路自适应模糊控制器设计

上节基于轨迹线性化方法设计了快回路控制器，在一定程度上削弱了快回路中不确定性带来的影响，并减小了附加到慢回路中的不确定性输入Δx1。同时，针对慢回路存在的参数摄动和外界扰动，以及从快回路引入的不确定性输入Δx1与前二者之间的耦合影响，必须设计有效可靠的慢回路控制器。

慢回路动态方程:

其中，

式中 Ω2为慢回路中的总的不确定性。

假设1 期望轨迹ydi，(i=1，2，3)有界，一阶导数存在且为光滑函数。定义跟踪误差:

得

采用动态逆控制律，则:

其中，Ks=diag(k1，k2，k3)(ki＞0，i=1，2，3)。

若所有扰动不存在，即Ω2=0，将式(16)代入慢回路动态方程(13)得

因此，当无外界扰动且f2(x2)和g2(x2)已知时，控制律(16)可使系统稳定。但在实际系统中，f2(x2)和g2(x2)是时变、非完全可知的，同时扰动Ω2也不为零，因此采用模糊系统逼近非线性函数 f2(x2)和g2(x2)，并引入鲁棒控制项来抵消逼近误差和外部扰动的影响。

3．1 自适应模糊模型逼近

模糊逻辑系统由一系列“如果—则—”的模糊规则组成，其中第i条规则为

由于模糊产生器、模糊推理机和模糊消除器各自都有不同的选取方法，因此把它们组合起来就可构成多种模糊逻辑系统，本文选择由乘积推理规则、中心平均模糊消除器、高斯型隶属函数构成的模糊逻辑系统。引入模糊基函数 ξ(x)=［ξ1(x)，…，ξm(x)］T:

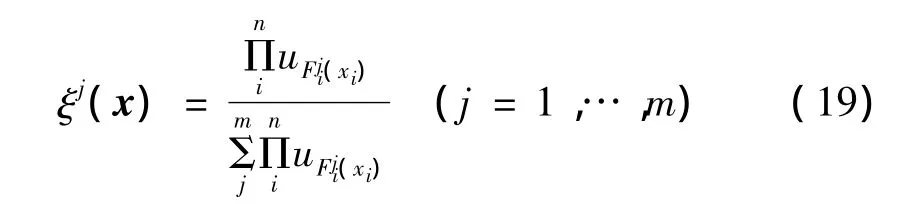
故y(x)=ξ(x)Tθ。则设计用于逼近未知非线性函数f2i(x2)和g2ij(x2)的模糊系统为

式中 ξfi和 ξgij是模糊基函数向量;θfi和 θgij是自适应调节参数向量。

设θfi和θgij的最优逼近参数为和，最小模糊逼近误差为εfi和εgij，其定义如下:

假设紧集Dx足够大，保证对所有的x∈Dx，最小逼近误差有界，即为已知常量。

令:

式中 ε0为任意小的正实数;I为单位阵。

由于在实际系统中，往往无法确定模型最小逼近误差的界，为此在不依赖建模误差上界，的情况下，本文采取在线估计的自适应模糊控制方法［7］。

3．2 慢回路控制器设计

对慢回路设计的控制律:

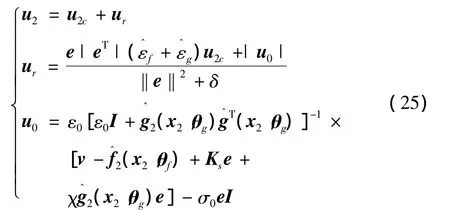
式中 ur为自适应鲁棒补偿项;u2c用式(16)表示。

自适应律:

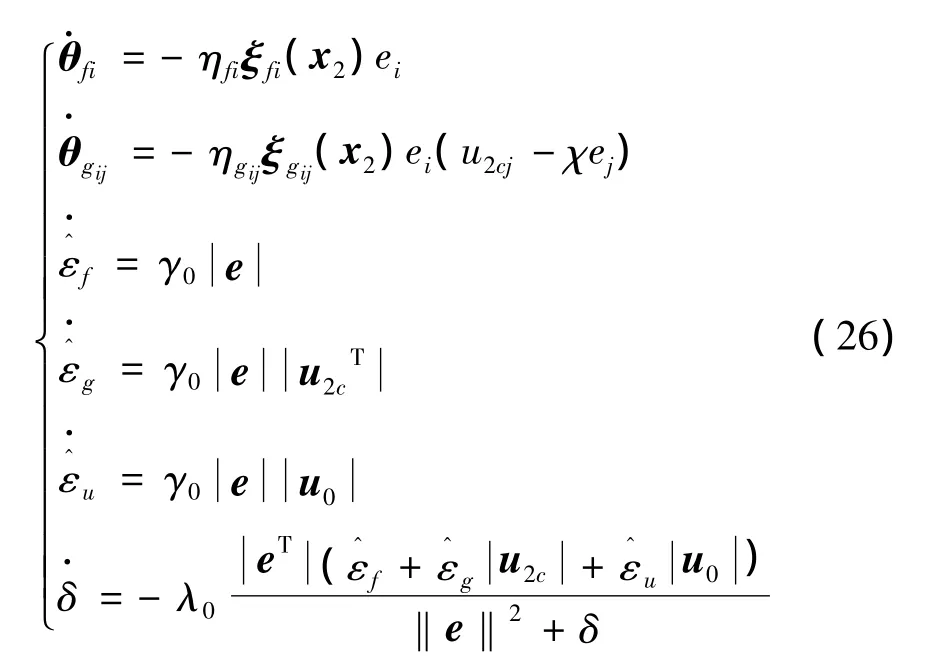
式中 χ，ηfi，ηgij，γ0，λ0均大于零;分别为的估计值。

根据文献［11］，可推导出慢回路在本文设计的带鲁棒补偿项的自适应模糊控制律的控制下，闭环系统的所有信号有界，并且在有限时间内，轨迹跟踪误差及其误差一阶导数均趋于零。

4 仿真验证

为验证本文设计的自动驾驶仪，分别设计了自适应模糊动态逆控制器(AFDI)和自适应模糊TCL控制器(AFTCL)，并在Matlab环境下进行仿真比较。初始条件 γ =5°，α =0°，β=0°，姿态角速率 x1=［0 0 0］T;舵偏u1=［0 0 0］T。三通道的控制指令分别取为:γc=0°，αc=20sin(0．5t+0．5)，βc=15sin(t)。在仿真中，气动参数的随机摄动范围为30%，并分别在在快、慢回路中加入均值为0、方差为0．04的随机噪声。

2种控制器的模糊基函数向量ξfi和ξgij的高斯型隶属度函数均取为

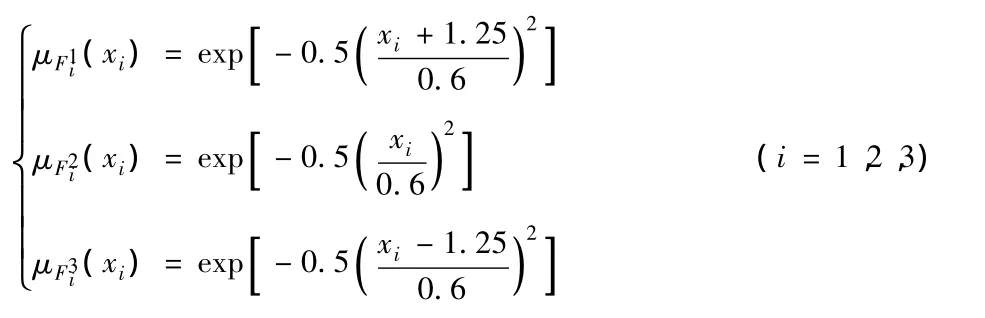
仿真得上述2种控制方式下三通道的响应对比曲线如图1～图3所示。

图1给出了三通道的控制指令的响应曲线。从图1可以看出，这2种控制器都有较快的响应速度，但AFDI在快变量较小时表现出来的抗干扰能力明显不如AFTCL，故本文采用的方法具有较强的鲁棒性。

图2给出了三通道的快变量的变化曲线。由图2可知，较之AFDI，AFTCL作用下的快变量的值稍大一些，但走势较为平滑，表明该控制器稳健的跟踪性能。

图3给出的三通道的舵偏控制量的变化曲线。由图3可知，2种控制器的舵偏控制量均满足要求，但快变量较小时AFTCL的舵偏控制量要大于AFDI的舵偏控制量，说明AFTCL在获得较好的跟踪效果的同时， 也相应需要消耗较多的能量。

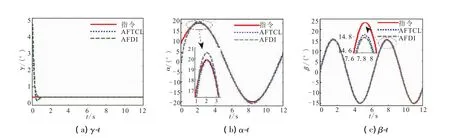
图1 三通道控制指令响应曲线Fig．1 Curves of three-channel command response

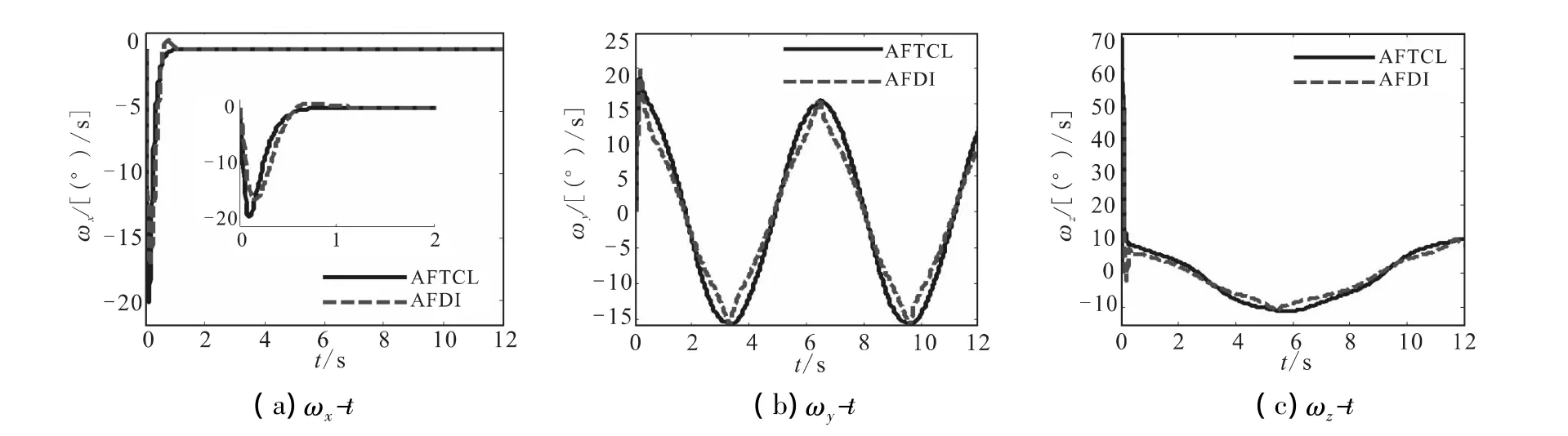
图2 快变量变化曲线Fig．2 Curves of fast variable

图3 舵偏角控制量变化曲线Fig．3 Curves of rudder deflection angle

5 结论

(1)轨迹线化方法既能快速跟踪控制指令，又能减弱外界扰动对系统的影响。

(2)在最小逼近误差界未知的情况下，通过在线自适应调节的方法获得估计值，此方法与直接假定的方法比较，具有适用性更广，也更加合理。

(3)在最小逼近误差界未知的情况下，本文设计的自适应鲁棒补偿项能够有效消除逼近误差。

(4)该自动驾驶仪的控制指令跟踪能力随快变量的增大而增强。当快变量变小时，指令跟踪误差变大，舵偏控制输出也相应变大，但总体上舵偏控制输出较小，能够满足控制要求。

(5)仿真结果表明，与自适应模糊动态逆控制器相比，自适应模糊TCL控制器具有更强的鲁棒性，提高了自动驾驶仪的性能。

［1］ 李惠峰．高超声速飞行器制导与控制技术［M］．北京:宇航出版社，2012．

［2］ Tony A Adami，Zhu J Jim．Flight control of hypersonic scramjet vehicles using a differential algebraic approach［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit，2006-6559

［3］ 李海军，黄显林，葛东明．再入机动飞行器自适应轨迹线性化控制［J］．宇航学报，2011，32(5):1039-1046．

［4］ 杨志峰，雷虎民，李庆良，等．基于轨迹线性化方法的导弹动态逆控制系统设计［J］．固体火箭技术，2011，34(1):1-5．

［5］ Navid N，Mehdi R M，Zol Ghadri J．Adaptive fuzzy sliding mode control scheme for uncertain systems［J］．Commun Nonlinear Sci Numer Simulat，2009，14:3978-3992．

［6］ 晋玉强，史贤俊，王学宝．基于神经网络的BTT导弹鲁棒动态逆控制［J］．系统工程与电子技术，2008，30(2):327-330．

［7］ 董飞垚，雷虎民，杨志峰，等．一种基于自适应模糊系统的导弹自动驾驶仪设计方法［J］．弹道学报，2011，23(1):84-87．

［8］ 薛亚丽．基于轨迹线性化方法的近空间飞行器鲁棒自适应控制研究［D］．南京航空航天大学．

［9］ 韩京清．自抗扰控制技术［M］．北京:国防工业出版社，2008．

［10］ Kahlil H K．Nonlinear systems［M］．2nd．ed．Prentice-Hall，Upper Saddle River，NJ，1996．

［11］ 曾宪法，张磊，申功璋．基于动态逆和分散控制的导弹控制系统设计［J］．北京航空航天大学学报，2007，33(11):1 303-1307．