固体发动机地面过载试验凝相粒子加速度分析①

许团委，田维平，王建儒，李 强

(1．西北工业大学航天学院，西安 710072;2．中国航天科技集团公司第四研究院，西安 710025;3．中国航天科技集团公司四院四十一所，西安 710025)

0 引言

当前，以美国“PAC-3”和俄罗斯“S-300V”为典型代表的小型战术导弹，由于其兼有反导拦截能力，故动力系统均采用强机动的高速高加速固体火箭发动机，主要技术特点是导弹在强机动过程中，要承受长时间小过载、中时间中过载、短时间大过载等，尤其是横向过载。导弹在大机动飞行过程中的高横向过载会引起燃烧室内凝相颗粒局部的高浓度聚集和冲蚀，使局部烧蚀加剧，对发动机热防护结构产生很大的影响，严重时导致壳体烧穿飞行失利［1－3］。大过载条件对燃烧室绝热层的烧蚀影响研究较多［4－6］，但对地面模拟过载试验时燃烧室的烧蚀区位置研究较少。

本文通过对燃烧室凝相粒子加速度理论分析、三维两相流数值计算及缩比发动机旋转模拟试验，初步分析了地面模拟过载试验中燃烧室粒子聚集区位置及旋转试验后烧蚀区位置，并对两种结果进行了对比，为飞行状态发动机热防护结构设计提供了参考依据。

1 过载模拟试验介绍

图1为高过载试验系统简图，该试验系统由动力源、旋转试车台、试验发动机和配重发动机组成。当试验发动机在试车台上旋转时，通过调节图1中旋转试车架的转速n和发动机倾斜角θ，可模拟发动机在不同轴向过载和横向过载条件下的工作过程。

以试验发动机中轴线上质点为计算点，计算得到离心加速度，即合成过载。

式中 ω为转动角速度;R为质心点回转半径。

通过分解合成加速度，即可得到期望模拟的横向加速度at=a·sinθ和轴向加速度an=a·cosθ。

图1 过载试验台装置示意图Fig．1 diagram of the overload test

2 粒子过载加速度理论分析

图2给出了地面发动机旋转试验的示意图。其中，为了建立计算模型及方便分析，选取y轴为旋转轴，发动机轴线与旋转轴之间的夹角为θ，发动机绕旋转轴旋转，角速度为ω，发动机燃烧室内某一颗粒的速度为=(vx，vy，vz)，位置为=(xp，yp，zp)。

图2 x-y-z坐标系下的加速度分解Fig．2 Acceleration resolution at x-y-z coordinate system

由图2可知，在地面旋转试验中，燃烧室内粒子受到的加速度有离心加速度、哥氏加速度以及由气相阻力产生的加速度。下面在x-z平面中，如图3所示，分别分析离心加速度和哥氏加速度。

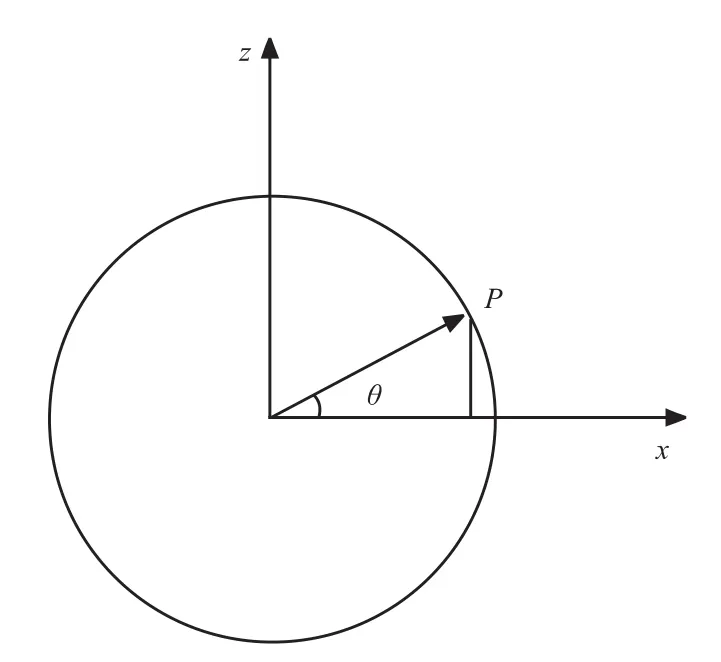
图3 x-z平面中的加速度分解Fig．3 Acceleration resolution in x-y plane

2．1 离心加速度

在发动机旋转过程中，颗粒受到的离心加速度计算方法如下，方向平行于旋转平面指向外侧。

写成空间矢量形式:

式中 an=ω2r;β由颗粒的相对位置确定。

2．2 哥氏加速度

同样，根据哥氏加速度的定义，在选取y轴为旋转轴的条件下，哥氏加速度的计算方法:

2．3 气相阻力产生的加速度影响

考虑气相阻力时，气相阻力为

式中 ρ为气相密度;dp为粒子的直径;CD为阻力系数。

3 粒子各项加速度对比分析

在x-y-z坐标系下，比较a0、ac与ag的大小。以模拟横向过载为6．0 g，轴向过载为13 g的旋转试验来看，其模拟的状态:

轴向加速度 an=127．4 m/s2，侧向加速度 aL=58．8 m/s2，倾斜角 α=24．79°，旋转半径 R=0．81 m，旋转速度ω=13．3 rad/s，电机转速n=127 r/min。以位于旋转半径端头处沿发动机轴线运动的颗粒为例，假设粒子速度为20 m/s，气相速度为18 m/s，颗粒受到的加速度写成空间矢量形式:

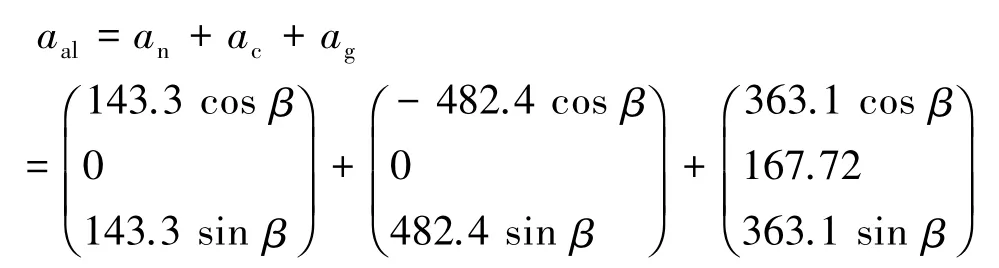
上式给出在某一旋转条件下燃烧室一任意颗粒受到的加速度计算式。可看出，计算结果与大小颗粒的相对位置β有很大关系。针对各项加速度求模，得出哥式加速度约为离心加速度的3．37倍，气相阻力由气体本身对凝相粒子产生的拖拽力而形成，是一种固有属性。所以，初步认为在旋转试验中，真正发挥巨大作用的是哥氏加速度和气相阻力的作用，离心加速度的作用并不占优。

4 数值计算与试验结果对比分析

在地面模拟过载试验中，不可避免会引入哥氏加速度。本章针对3组不同过载下的缩比发动机，分别开展了三维两相流数值计算，并进行了地面旋转模拟过载试验，发动机受过载工况见表1。通过分析计算得到的关键参数，如粒子聚集浓度、冲刷速度、粒子沉积区位置，以及试验解剖获得的烧蚀区位置，对前面理论分析结果进行了验证分析。

表1 发动机过载试验工况Table 1 Overload test condition

4．1 数值计算分析

为了使数值计算结果能反映地面试验结果，需要在数值计算中，综合考虑旋转加速度a0与哥氏加速度ac。考虑旋转加速度和哥氏加速度，发动机装药燃面退移1/2;粒径分布取10～150 μm，平均直径为70 μm。

(1)工况1

颗粒冲刷严重的部位距装柱后端面200 mm的位置，聚集浓度约为16 kg/m3，冲刷速度约为13 m/s，冲刷角度约为11°，分布于Ⅰ偏Ⅳ象限约为62°。粒子浓度分布如图4(a)所示。

(2)工况2

颗粒冲刷严重的部位距装柱后端面146 mm的位置，聚集浓度约为22 kg/m3，冲刷速度约为16 m/s，冲刷角度约为15°，分布于Ⅰ偏Ⅳ象限约为69°。粒子浓度分布如图4(b)所示。

(3)工况3

颗粒冲刷严重的部位距装柱后端面125 mm的位置，聚集浓度约为27 kg/m3，冲刷速度约为17 m/s，冲刷角度约为15°，分布于Ⅰ偏Ⅳ象限约为73°。粒子浓度分布如图4(c)所示。

图4 粒子聚集浓度分布云图Fig．4 Distribution contours of particle concentration

通过对3种不同过载工况进行计算，获得粒子冲刷参数，见表2。可发现，沿装药后端面向喷管方向看，随着横向过载的逐渐增大，粒子聚集位置由燃烧室中后部向装药后端面方向移动，分布于Ⅰ偏Ⅳ象限62°～73°之间，聚集浓度和冲刷速度逐渐增大，但变化不大，冲刷角度维持在11°～15°之间。

4．2 试验结果与计算结对比分析

地面旋转试验发动机装置示意图见图1。表3针对数值计算结果中粒子浓度聚集区位置与试验后的烧蚀位置进行了对比。

表3 数值计算与试验结果对比Table 3 Comparison of numerical and experimental results

从表3可看出，旋转试验解剖后的结果反映了颗粒冲刷严重部位及烧蚀严重部位维持在第Ⅰ象限偏第Ⅳ象限70°～90°之间;数值计算得到的粒子沉积区维持在第Ⅰ象限偏第Ⅳ象限60°～80°之间。尽管两种结果之间存在差异，但都说明了烧蚀严重区没有位于离心方向，而是由离心方向向旋转方向偏转，同时也反映了哥氏加速度在试验及计算中对凝相粒子的影响远大于离心加速度的影响。因此，过载发动机的地面旋转模拟试验不能精确地模拟实际飞行过载工况，需要剥离掉离心加速度以外其它加速度对凝相粒子的影响。

5 结论

(1)地面旋转过载试验中，燃烧室凝相粒子主要受哥氏加速度和气相阻力的作用，离心加速度的作用并不占优。

(2)数值计算得到的粒子沉积区维持在第Ⅰ象限偏第Ⅳ象限60°～80°之间;旋转试验解剖后的结果反映了颗粒冲刷严重部位及烧蚀严重部位维持在第Ⅰ象限偏第Ⅳ象限70°～90°之间。两种结果具有一定吻合性。

(3)过载发动机的地面旋转模拟试验不能精确地模拟实际飞行过载工况，需要剥离掉离心加速度以外其它加速度对凝相粒子的影响。

［1］ 何国强，王国辉，蔡体民，等．高过载条件下固体发动机内流场及绝热层冲蚀研究［J］．固体火箭技术，2001，24(4):4-8．

［2］ 武渊，何国强，孙展鹏，等．过载对固体火箭发动机性能影响试验研究［J］．固体火箭技术，2010，33(5):511-514．

［3］ 李越森，叶定友．高过载下固体发动机内A12O3粒子运动状况的数值模拟［J］．固体火箭技术，2008，31(1):24-27．

［4］ 李江，何国强，秦飞，等．高过载条件下绝热层烧蚀实验方法研究(Ⅰ)方案论证及数值模拟［J］．推进技术，2003，24(4):315-318．

［5］ 李江，何国强，陈剑，等．高过载条件下绝热层烧蚀实验方法研究(Ⅱ)收缩管聚集法［J］．推进技术，2004，25(3):196-198．

［6］ 刘世东．过载对固体火箭发动机影响的研究［J］．航空兵器，2006(6):42-44．