一种空空导弹攻击区的快速解算方法①
2014-01-16王志刚
王志刚,张 宁,李 伟
(1.西北工业大学 航天学院,西安 710072;2.航天飞行动力学技术重点实验室,西安 710072)
0 引言
传统的攻击区解算会占用大量计算资源,影响导弹作战效能。为解决计算精度和快速解算的矛盾,需要研究面向工程应用的攻击区快速解算方法。不同于张平等[1-5]通过单独采用黄金分割或变步长积分算法来提高攻击区的解算速度,本文从积分算法、气动力系数计算及最大最小边界的确定着手,结合三自由度弹道模型,建立了一种空空导弹攻击区快速解算方法。
本文选择解算速度更优的变步长积分法[3]进行弹道积分;采用多项式拟合方式处理已知气动系数数据,避免了传统插值算法的数据搜索耗时[6-8];最大最小边界的确定则结合了空空导弹可攻击区多项式拟合与黄金分割法,用多项式拟合结果作为边界值的预估值,构成黄金分割法的初始搜索区间,从而减少了边界搜索循环次数,提高了可攻击区的计算速度。最后通过具体的仿真实验论证了该算法的可行性。
1 攻击区快速计算方法
1.1 积分算法
变步长求积法的基础是复化梯形公式,但不是先确定对积分区间的细分数,而是根据精度要求逐步将区间细分。为了尽量避免被积函数值的重复计算,在细分的过程中总是对原先的小区间再二等分一次,以便充分利用原来结点上的函数值。因此,与龙格库塔法相比,变步长积分法具有快速计算的优点。其求解过程如下:
首先利用梯形公式(1)计算积分值:
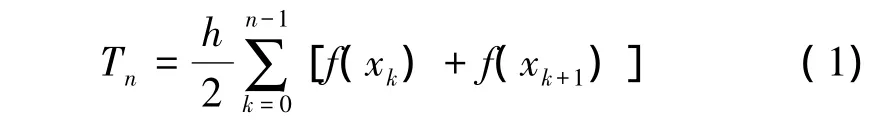
将每一个求积区间二等分:
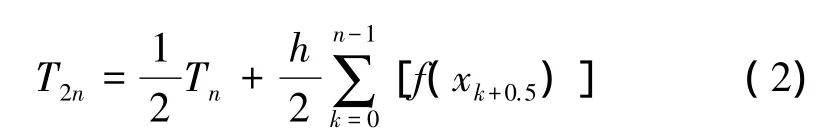
然后对二等分前后2次的积分值进行判断(式(3))来确定是否满足精度要求:
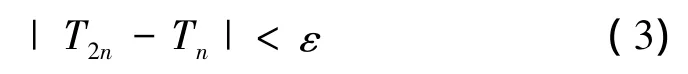
若满足精度,则终点时刻状态值由式(4)得出:

反之,则保存当前的等分数、积分值与步长,对积分区间继续做二等分处理,即:
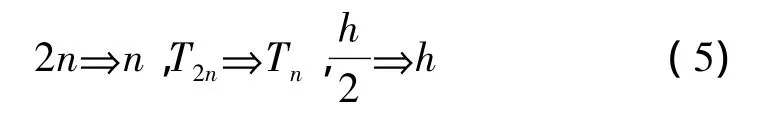
1.2 气动力系数计算
利用传统插值算法对气动数据进行计算时,虽能保证一定的精度,但不具有快速性。因此,在本文的研究中选择采用气动力系数的多项式拟合来实时计算导弹的气动力系数。
参考美国AIM-120空空导弹外形参数,首先利用DATCOM软件进行气动系数计算,然后通过拟合软件对其拟和,得到式(6):

式中 p1~p11为拟合参数。
升力系数原始数据和拟合数据如表1所示。
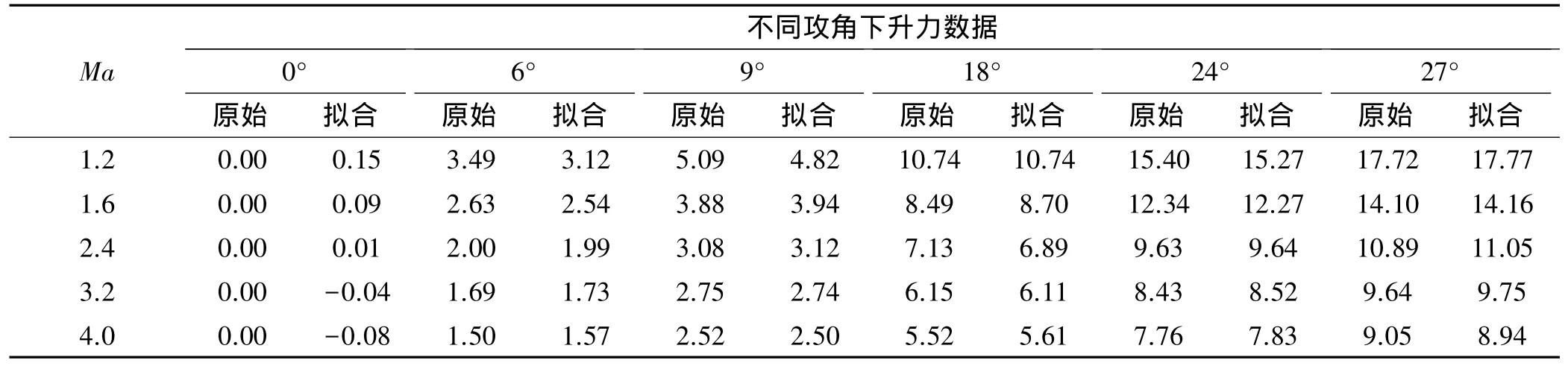
表1 升力系数原始数据及拟合数据Table 1 Original data and fitting data of lift coefficient
由表1可看出,与原始数据相比,拟合结果具有较高的精度,但该组数据在攻角为0°时偏差较大。因此,在仿真过程中直接将α=0°的升力系数值取零。另外,若计算负值攻角下的升力系数,只要在Cy的基础上乘以-1即可。
1.3 最大最小边界的确定
本文采用的攻击区边界快速搜索算法与传统的逐步搜索法相比,其初始搜索范围已接近于可攻击区允许发射距离值,因而在解算过程中可减少搜索循环次数,提高攻击区的求解速度。下面以最远边界为例,介绍该算法的计算过程。
(1)可攻击区多项式拟合
首先针对空战中可能遇到的各种情况,根据导弹数学模型进行离线仿真后再利用拟合算法进行数据处理,就得到攻击区远界的拟合多项式,由于该拟合结果是作为攻击区边界值的预估值,因此只需要拟合误差在一定范围内而不要求其精度相当高。
(2)黄金分割法下的边界搜索
在一维搜索中,黄金分割法[9]同其他方法相比不需要事先知道计算次数,而且收敛速率较快,因此本文利用该搜索法对导弹攻击区边界进行精确搜索。
下面同样以远边界为例进行说明:首先,以载机为中心,选定目标的方向,根据确定初始搜索范围[a0,b0],计算黄金分割点 Rg=a0+0.618(b0-a0);然后,在分割点位置进行数值积分并根据弹道仿真结束条件判断导弹是否命中目标,若击中目标,则令ai=Rg,bi=bi-1;否则令 ai=ai-1,bi=Rg,重新进行循环计算,直至求出满足所有约束条件的边界为止。
具体计算流程如图1所示。
2 导弹的运动模型
为进一步提高攻击区的解算速度,选用三自由度数学模型来描述导弹的空间运动。
2.1 基本假设
(1)将导弹视为质点运动,并满足瞬时平衡假设;
(2)在步长时间内,导弹各参数保持不变;
(3)目标运动规律已知;
(4)采用标准大气数据;
(5)导弹滚转稳定,且速度倾斜角为零。
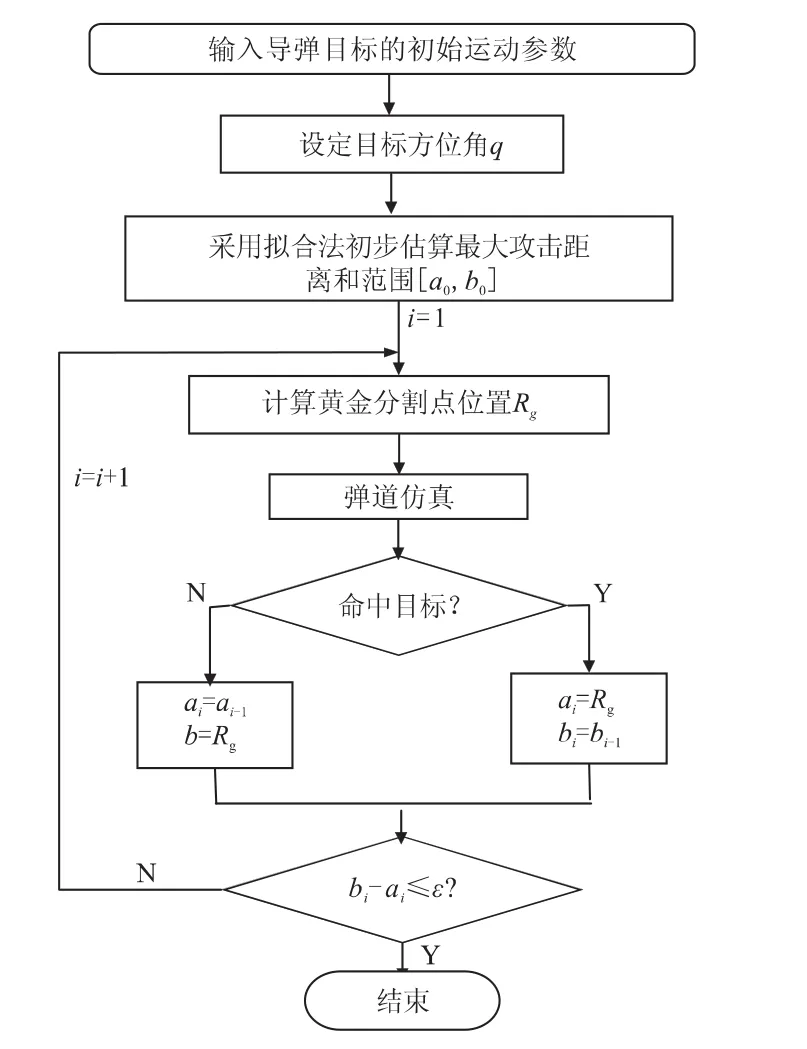
图1 远距离搜索流程图Fig.1 Flow chart for remote distance search
2.2 导弹运动学方程
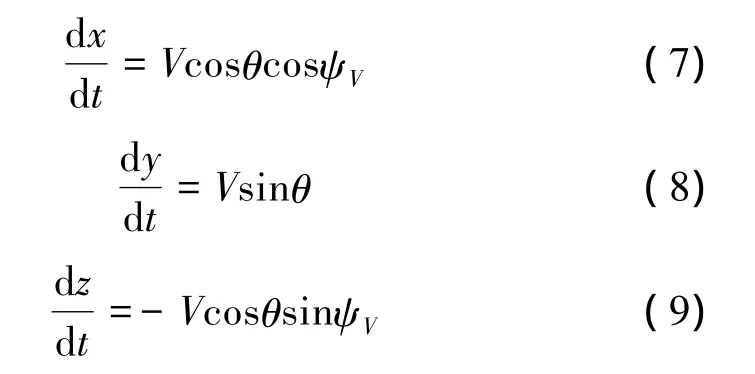
式中 V、θ、ψV分别为导弹的速度、弹道倾角和弹道偏角;x、y、z为导弹质心在地面坐标系中的坐标。
2.3 导弹动力学方程
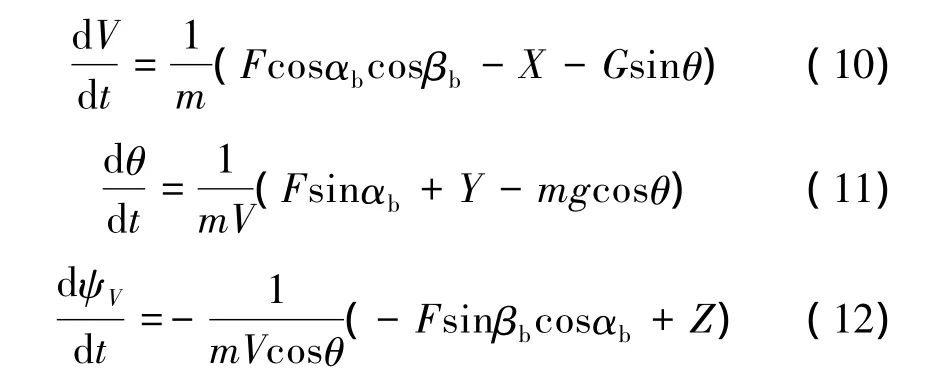
式中 X、Y、Z分别为导弹受到的阻力、升力和侧向力;F为发动机推力;m为导弹质量;αb、βb分别为平衡攻角和平衡侧滑角。
2.4 导引方程
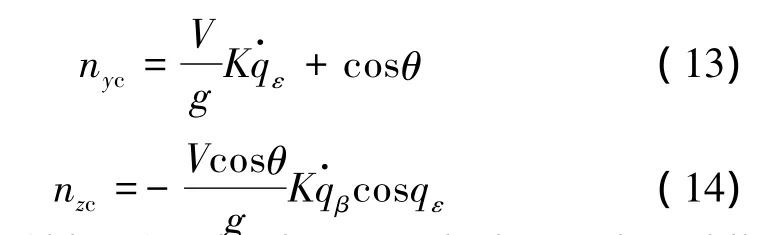
式中 K为比例导引系数;g为重力加速度;qε为目标视线高低角;q·β和q·ε分别为目标视线方位角和高低角的偏转角速度;nyc、nzc分别为导弹在垂直方向和横向的控制过载。
2.5 控制方程
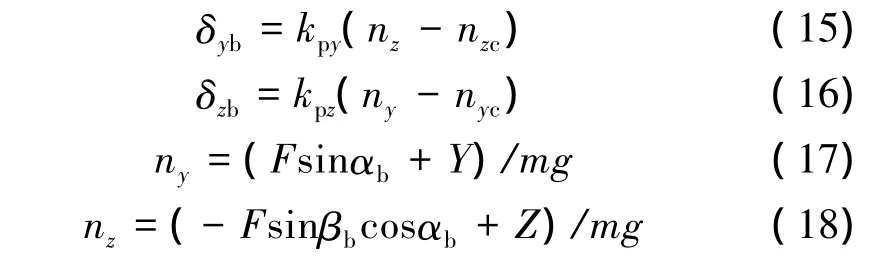
式中 kpy、kpz为控制系数;ny、nz分别为导弹在垂直方向和横向的过载;δyb为方向舵的平衡舵偏角;δzb为升降舵的平衡舵偏角。
2.6 瞬时平衡关系
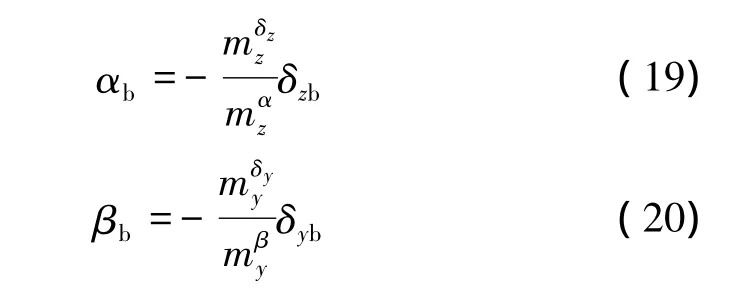
2.7 目标运动方程
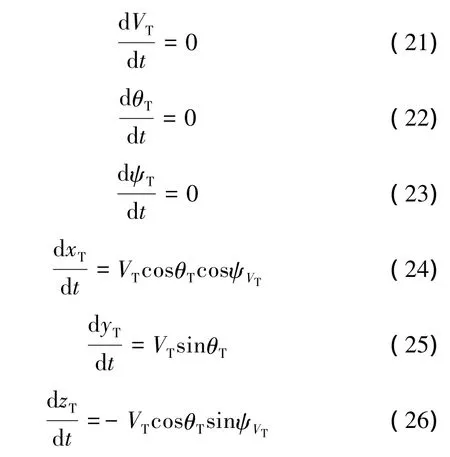
式中 VT、θT、ψVT分别为目标运动速度、弹道倾角和弹道偏角;xT、yT、zT为目标质心在地面坐标系中坐标。
2.8 相对运动方程

式中 r表示导弹与目标之间的相对距离;qβ为视线方位角。
3 仿真计算与分析化
3.1 仿真条件
仿真过程中的攻击区计算均是在以下条件下进行的:导弹与目标的初始飞行高度相同;仿真过程中的循环条件只取进入角qβ。具体的初始条件如下:
(1)目标运动状态:VT=414.36 m/s,θT0=0°,ψVT0=180°,yT=10 km。
(2)导弹初始运动状态:V=414.36 m/s,θ0=0°,ψV0=0°,x0=0 km,y0=10 km,z0=0 km。
3.2 攻击区边界的多项式拟合
首先以AIM-120为对象,利用Visual C++进行仿真计算得到传统算法下 qβ∈(-36°,36°)时的理论攻击区。然后对其边界值进行多项式拟合,结果如下:
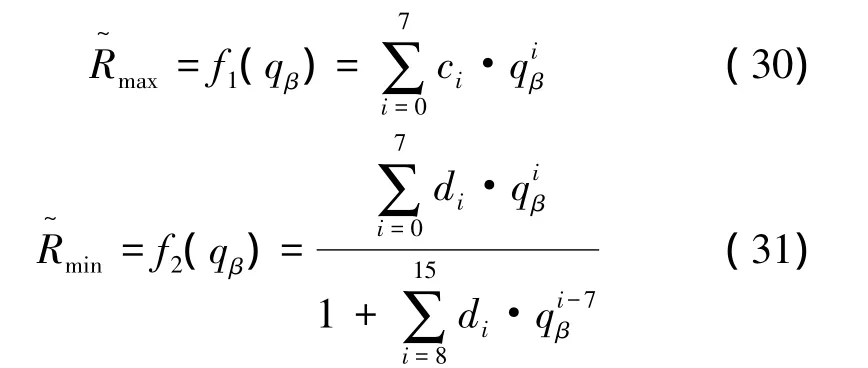
式中 ci、di均为拟合参数为攻击区近边界的拟合多项式。
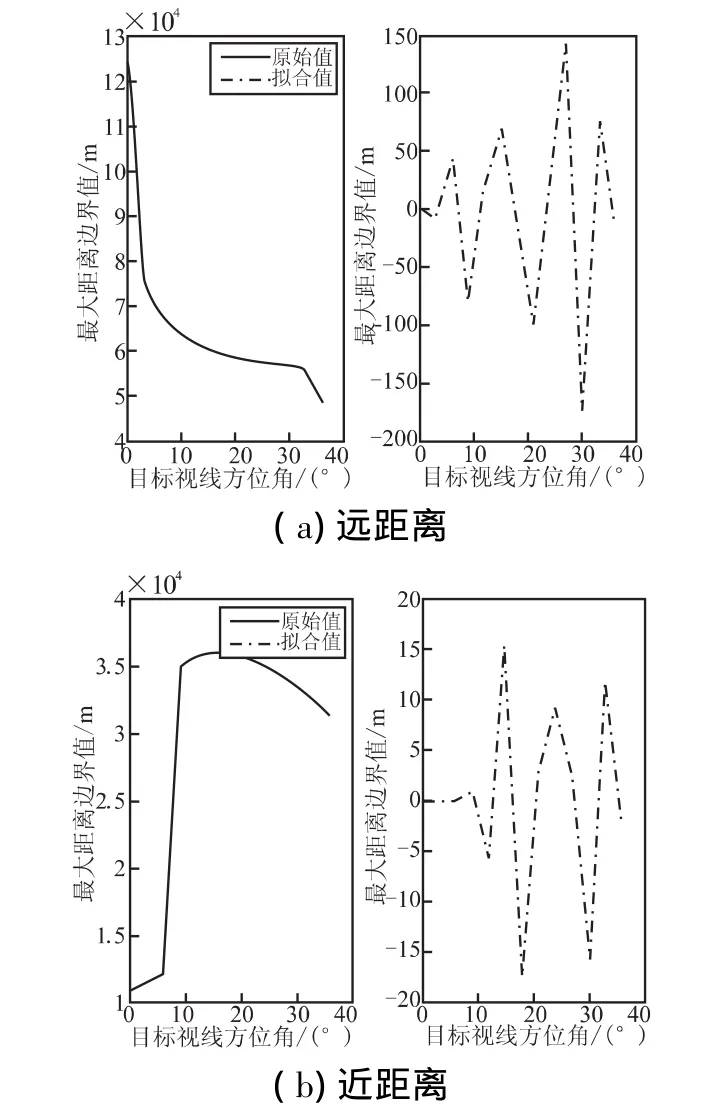
图2 远距离、近距离的边界拟合数据对比Fig.2 Fitting data comparison of remote boundary and close range boundary
3.3 攻击区仿真
通过在同一台2G内存、双核2.5GHz赛扬处理器的计算机上对第1节中的3种快速解算方法进行攻击区解算,并将仿真结果与理论攻击区在同一坐标系下作图,结果如图3~图6所示。其中,图3~图5分别为单独采用变步长算法、气动拟合算法和边界快速搜索算法下的攻击区对比;图6为将以上3种算法与三自由度运动模型相结合后仿真得到的攻击区对比结果。
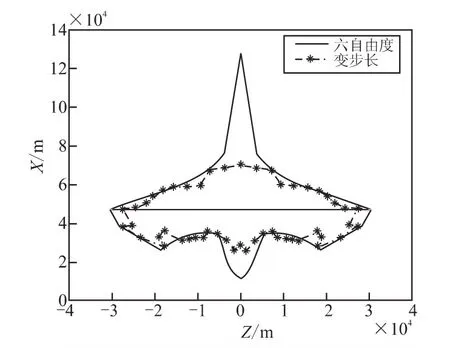
图3 变步长模拟攻击区对比Fig.3 Comparison of attacking area simulation step-changed method
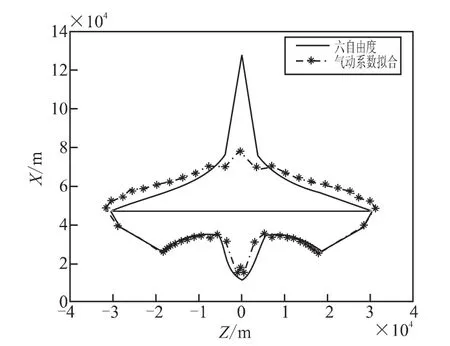
图4 气动拟合模拟攻击区对比Fig.4 Comparison of attacking area simulation by pneumatic fitting method
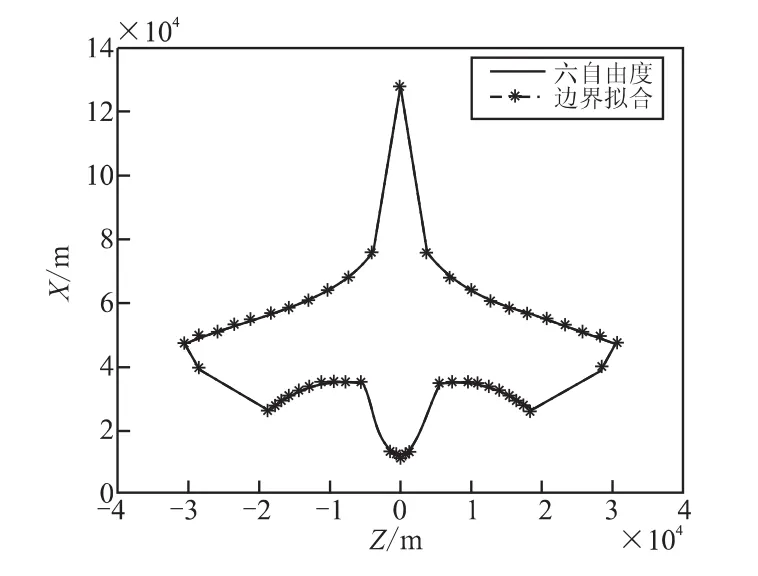
图5 边界快速搜索模拟攻击区对比Fig.5 Comparison of attacking area simulation by boundary fast search method
3.4 结果分析
首先利用平均成功发射概率的概念对图3~图6中的模拟攻击区进行精度验证,得出对应不同算法下的失机发射概率Pml、边界外发射概率Pob和平均成功发射概率P,结果如表2所示。表3为各算法下攻击区解算时间的对比。
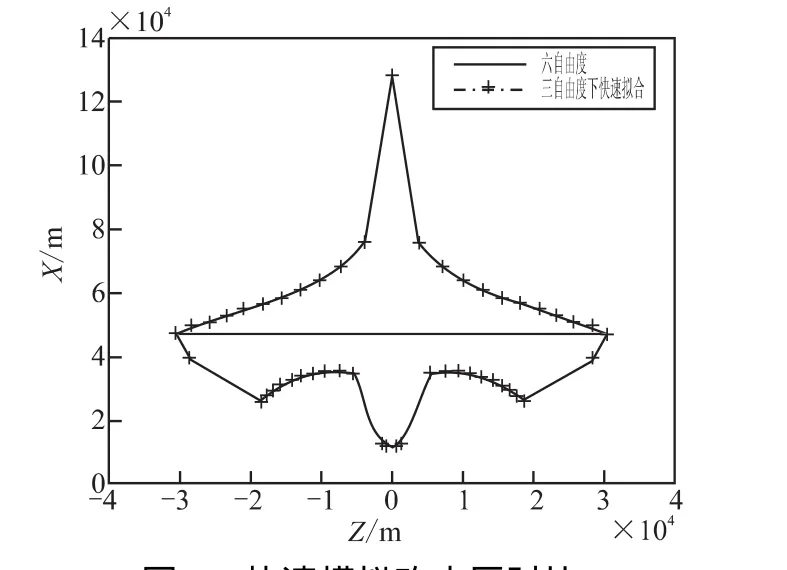
图6 快速模拟攻击区对比Fig.6 Comparison of attacking area simulation by fast method
通过以上对比结果可看出:
(1)变步长积分算法虽能提高解算速度,但该算法对仿真结果的精度产生了很大影响,使得实际面积远小于理论攻击区,增大了失机发射概率。经过分析可知造成这种误差的原因在于该算法是通过对比相邻2次的计算结果来判断是否达到精度要求,而不是与精确解进行对比。
(2)气动系数拟合下的解算速度与插值算法相比提高了近22倍,但从其计算精度可以看出气动力系数的高精度拟合并不能保证模拟攻击区的高精度解算。
(3)与气动系数拟合和变步长积分算法相比,边界的快速搜索算法不仅有效提高到了攻击区的解算速度,还保证了较高的计算精度。这是因为相对于理论攻击区的计算,该算法的使用只改变了初始搜索区间的范围,而未改变仿真过程中的算法,因此只要初始搜索区间选取合适,就能够通过黄金分割法快速准确地求出攻击区的边界值。
(4)从图6和表1、表2的对比结果可看出,本文所建立的空空导弹攻击区快速解算方法不仅弥补了变步长与气动拟合算法下的误差,还在保证边界快速搜索算法的高精度基础上,进一步提高了计算速度。
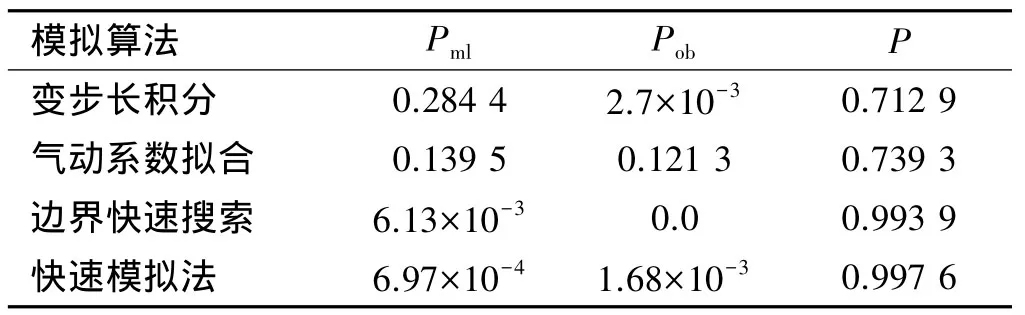
表2 不同算法下攻击区精度比较Table 2 Comparison of attacking area accuracy by different methods

表3 不同算法下攻击区解算时间Table 3 Comparison of attacking area simulation time by different methods
4 结论
(1)单独采用变步长算法、气动系数拟合算法代替四阶龙格库塔法和传统二元三点插值算法进行攻击区解算时均能有效减少计算时间,但会产生较大误差。
(2)攻击区的边界快速搜索算法利用其计算原理能够有效提高攻击区的解算速度和精度。
(3)将3种算法与导弹三自由度运动模型相结合后得到的空空导弹攻击区快速解算方法不仅弥补了单独使用一种快速算法时的不足,而且有效地提高了计算速度。从而保证了机载武器系统的实时性要求,对火控系统实时解算攻击区边界具有参考意义。
[1] 张平,方洋旺,肖冰松,等.空空导弹攻击区实时解算的新方法[J].弹道学报,2010,22(4):11-18.
[2] 周灿辉,周德云,何鹏,等.中程空空导弹可攻击区解算的新方法[J].火力与指挥控制,2012,37(7):54-60.
[3] 吕铭强,张安.中程空空导弹火控系统评定基准研究[J].系统工程与电子技术,2003,25(10):1307-1310.
[4] 杜昌平,周德云,江爱伟.一种空空导弹可攻击区快速算法[J].西北工业大学学报,2006,24(6):682-685.
[5] 黄家成,张迎春,罗继勋.空空导弹攻击区的快速模拟法求解[J].弹箭与制导学报,2003,23(4)132-134.
[6] 程毛林.数据拟合函数的加权最小二乘积分法[J].数学的实践与认识,2012,4:011.
[7] 吕喜明,李明远.最小二乘曲线拟合的MATLAB实现[J].内蒙古民族大学学报:自然科学版,2009,24(2):125-127.
[8] X Yang,G Wang.Planar point set fair and fitting by arc splines[J],Computer-Aided Design,2001,33:35-43.
[9] 陈宝林.最优化理论与算法[M].北京:清华大学出版社,2007:256-259.
